题目:大家都知道斐波那契数列,现在要求输入一个整数n,请你输出斐波那契数列的第n项(从0开始,第0项为0)。
一 . 理解概念
斐波那契数列概念:斐波那契数列(Fibonacci sequence),又称黄金分割数列,因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”(来自百度百科)。具体可由以下公式表示:
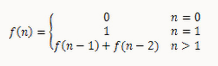
二.C#代码如何实现
由上述公式可知,斐波那契数列存在两个特殊值,即当n=0和n=1时,因此,可将n等于0与1时提出来作单独处理,而剩下的部分再作单独处理,基于这种想法,实现该目标可使用两种方法:
方法1:递归法。
斐波那契数列是递归法最典型的一种体现,但又存在着很多的不足。
其中,递归的实现是通过调用函数本身,函数调用的时候,每次调用时要做地址保存,参数传递等,这是通过一个递归工作栈实现的。具体是每次调用函数本身要保存的内容包括:局部变量、形参、调用函数地址、返回值。那么,如果递归调用 N 次,就要分配 N*局部变量、N*形参、N*调用函数地址、N*返回值,这势必是影响效率的,该题目中,用递归方法计算的时间复杂度是以n的指数的方式递增的,此段来自Edison Zhou的博文。
如下代码是使用递归实现的斐波那契数列(该题目中可以看出,若你>1,计算f(n)需要不断重新的调用Fibonacci函数):
class Solution{ public int Fibonacci(int n) { //当n小于等于0时,返回0 if (n <= 0) { return 0; } //当n等于1时,返回1 if (n == 1) { return 1; } //否则,返回前两个数之和 else { return Fibonacci(n - 1) + Fibonacci(n - 2); } } }
很显然,递归虽然可以实现斐波那契数列,但却存在着一定的问题。
方法二 : 循环法。
由于递归存在着效率低问题,为解决该问题,引入循环的方法避免了递归法重复计算的弊端,从而运算的时间复杂度变为是O(n)。
具体实现代码如下:
class Solution { public int Fibonacci(int n) { // write code here int x = 0; int y = 1; int result = 0; if (n == 0) { return 0; } if (n == 1) { return 1; } else { for (int i=2;i<=n;i++) { result = x + y; x = y; y = result; } return result; } } }
上述代码在实现上与递归法大同小异,不同点在于不需要重复的调用函数,个人感觉理解起来更加容易一点。