我们现在说Recursive backtracking:
- 迷宫的初始状态是墙壁都存在。选择一个开始区域。
- 随机得选择一个没有访问过的邻接区域,并打通与它之间的墙壁。此邻接区域称为当前区域。
- 如果所有周围的区域都是访问过的,则退回上一个区域进行挖据墙壁,一直重复。
- 当开始的区域被退回的时候,算法结束。
大家都知道,至于迷宫的求解问题,可以用穷举法进行求解。那么什么是穷举法了,就是将每一种可能的情况都穷举完。而具体到迷宫的求解问题上,由于在求解过程中可能会遇到某一路径不可行的情况,此时我们就必须按原路返回,这时自然也就会想到栈的应用了,因为栈的一个很重要的特性就是”先进后出”,可以用来记录每次所探索的路径,方便在原路返回的过程中,得到上一步所走路径,再按此方法,退回到可以走得通的位置上,继续探索下去,直到到达终点或者最终无法到达,正常退出程序为止。
下面我们现在首先定义一下有关迷宫求解过程中运用到的相关定义与技巧吧!
1.我们规定每次探索的方向是把当前位置的相邻的东边位置作为第一个探索位置,若不通,则再逆时间方向探索之。具体地说就是右——上——左—— 下的方向进行探索。当然这个方向大家可以随意确定,只是确定后探索方向后,我们在下面编写确定下一位置的函数过程中得根据这个方向进行编码!当然迷宫的位置我们可以定义一个结构体表示,如:
1: typedef struct Postion 2: { 3: int x; 4: int y; 5: }Postion;
那么确定下一探索位置的函数我们可以这么编写:
01: struct Postion nextPos(struct Postion pos,int dir) 02: { 03: //contrarotate(¨逆?时±针?旋y转a)? 04: switch(dir) 05: { 06: case 1:pos.y+=1;break; 07: case 2:pos.x-=1;break; 08: case 3:pos.y-=1;break; 09: case 4:pos.x+=1;break; 10: default:break; 11: } 12: return pos; 13: }
2.我们定义一个顺序栈来存储探索过的路径,以便返回时得到上一次走过的位置。而栈元素主要记录了当前位置、步数以及下一探索方向,即:
1: typedef struct mazenode 2: { 3: struct Postion pos;//current location 4: int curstep;//current step number 5: int dir;//current direction 6: }mazenode;
接下来就是定义栈的各种典型操作呢,有初始化、进栈、出栈、是否为空判断等操作。(此步骤较简单,在此先不贴出代码了~)
3.最后让我们来理清一下迷宫求解过程的关键思想吧!
do
{
if(当前的路径可以通过)
{
留下足迹;
将当前位置保存并入栈
if(判断当前路径是否为最终路径)
{
退栈,并修改迷宫的数据,记录所走的路线
并返回 1;
}
当前步数增一;
获取下一位置;
}
else//当前位置走不通
{
if(当前栈不为空)
{
退栈;
while(当前位置的所走方向为4并且当
当前栈不为空)
{
记录当前位置不为走不通;
退栈处理;
当前步数减一;
}
if(当前的位置所走方向小于4)
{
将当前位置的方向增一;
将当前位置重新进栈;
获取下一将要通过的位置;
}
}
}
}
while(当前的栈不为空)
(注:当前的逻辑写得比较简单,各位看客们呆会看具体的源码哈!)
接下来我先贴一下有关栈的相关操作函数吧,主要包括典型的进栈
、出栈、判断栈是否为空等操作。
01: void initStack(struct Sqstack *s) 02: { 03: s->base=(struct mazenode **)malloc(STACK_INIT_SIZE*sizeof(struct mazenode *)); 04: if(!s->base) 05: { 06: printf("allocation fails!"); 07: exit(-1); 08: } 09: s->top=s->base; 10: s->stacksize=STACK_INIT_SIZE; 11: } 12: 13: void Push(struct Sqstack *s,struct mazenode * e) 14: { 15: if((s->top-s->base)>=STACK_INIT_SIZE) 16: { 17: s->base=(struct mazenode **)realloc(s->base,(STACK_INIT_SIZE+STACKINCREASE)*sizeof(struct mazenode *)); 18: if(!s->base) 19: { 20: printf("allocation fails!"); 21: exit(-1); 22: } 23: s->top=s->base+STACK_INIT_SIZE; 24: s->stacksize=STACK_INIT_SIZE+STACKINCREASE; 25: } 26: *s->top++=e; 27: } 28: 29: void Pop(struct Sqstack *s,struct mazenode **e) 30: { 31: if(s->base==s->top) 32: { 33: printf("the stack is empty!"); 34: exit(0); 35: } 36: *e=*(--s->top); 37: } 38: 39: int getTop(struct Sqstack *s,struct mazenode ** e) 40: { 41: if(s->base==s->top) 42: { 43: printf("the stack is empty!"); 44: return 0; 45: } 46: else 47: { 48: *e=*(s->top-1); 49: return 1; 50: } 51: } 52: 53: int emptyStack(struct Sqstack *s) 54: { 55: if(s->base==s->top) 56: { 57: return 1;//stack is empty! 58: } 59: else 60: { 61: return 0;//stack is not empty! 62: } 63: }
接下来是有关迷宫求解的“业务”规则代码吧!
01: int Pass(struct Postion pos,int array[MAZESIZE][MAZESIZE]) 02: { 03: if(array[pos.x][pos.y]!=0&&array[pos.x][pos.y]!=-1) 04: { 05: return 1;//indicate the way can pass 06: } 07: else 08: { 09: return 0;//indicate the way can not pass 10: } 11: } 12: 13: struct Postion nextPos(struct Postion pos,int dir) 14: { 15: //contrarotate(¨逆?时±针?旋y转a)? 16: switch(dir) 17: { 18: case 1:pos.y+=1;break; 19: case 2:pos.x-=1;break; 20: case 3:pos.y-=1;break; 21: case 4:pos.x+=1;break; 22: default:break; 23: } 24: return pos; 25: } 26: 27: 28: void markFoot(int arr[MAZESIZE][MAZESIZE],struct Postion pos) 29: { 30: arr[pos.x][pos.y]=0;//have pass by the way 31: } 32: 33: void markblock(int arr[MAZESIZE][MAZESIZE],struct Postion pos) 34: { 35: arr[pos.x][pos.y]=-1;//do not pass by the postion 36: }
然后是迷宫求解可走线路的核心算法:
01: int processMaze(int arr[MAZESIZE][MAZESIZE],struct Postion start,struct Postion end) 02: { 03: struct Sqstack s; 04: struct mazenode *p=(struct mazenode*)malloc(sizeof(struct mazenode)); 05: struct mazenode *nodelist=(struct mazenode *)malloc(100*sizeof(struct mazenode));//put down the way of sucess! 06: int curstep=1,flag=0; 07: struct Postion curpos=start,temp; 08: initStack(&s); 09: do 10: { 11: if(Pass(curpos,arr)) 12: { 13: markFoot(arr,curpos); 14: //struct mazenode node; 15: nodelist[flag].pos=curpos; 16: nodelist[flag].curstep=curstep; 17: nodelist[flag].dir=1;//towards east 18: Push(&s,nodelist+flag); 19: flag++; 20: if(curpos.x==end.x&&curpos.y==end.y) 21: { 22: while(!emptyStack(&s)) 23: { 24: Pop(&s,&p); 25: arr[p->pos.x][p->pos.y]=p->curstep; 26: } 27: return 1; 28: } 29: curstep++; 30: curpos=nextPos(curpos,1);//towards east 31: } 32: else 33: { 34: if(!emptyStack(&s)) 35: { 36: Pop(&s,&p); 37: while(p->dir==4&&!emptyStack(&s)) 38: { 39: markblock(arr,p->pos);//mark that the way is not passed 40: Pop(&s,&p); 41: curstep--; 42: } 43: if(p->dir<4) 44: { 45: p->dir++; 46: Push(&s,p); 47: temp=p->pos; 48: curpos=nextPos(temp,p->dir); 49: } 50: } 51: } 52: } 53: while(!emptyStack(&s)); 54: return 0;//failure 55: }
最后我们来实现下代码的可行性测试函数吧(说白了就是main函数啦)
01: int _tmain(int argc, _TCHAR* argv[]) 02: { 03: int maze[8][8]={{0,0,0,0,0,0,0,0},{0,0,1,0,0,1,0,0},{0,1,1,0,0,0,1,0}, 04: {0,1,0,0,0,0,0,0},{0,1,1,1,0,0,1,0},{0,0,0,1,0,0,1,0}, 05: {0,0,0,1,1,1,1,0},{0,0,0,0,0,0,0,0}},i,j,flag; 06: struct Postion start,end; 07: start.x=1;start.y=2; 08: end.x=4;end.y=6; 09: printf("primative maze: "); 10: for(i=0;i<MAZESIZE;i++) 11: { 12: for(j=0;j<MAZESIZE;j++) 13: { 14: printf("%2d",maze[i][j]); 15: } 16: printf(" "); 17: } 18: flag=processMaze(maze,start,end); 19: if(flag==1) 20: { 21: printf("maze processing success! "); 22: printf("processed maze: "); 23: for(i=0;i<MAZESIZE;i++) 24: { 25: for(j=0;j<MAZESIZE;j++) 26: { 27: printf("%2d",maze[i][j]); 28: } 29: printf(" "); 30: } 31: } 32: else 33: { 34: printf("maze processing fail! "); 35: } 36: return 0; 37: }
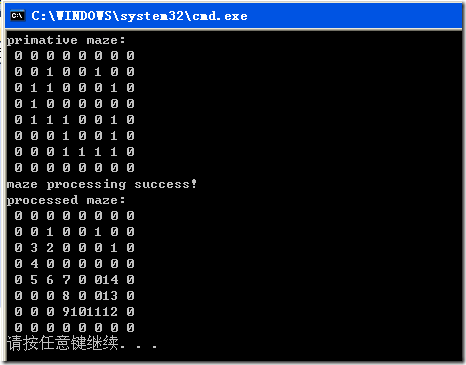
好了,最后让我们看看最终方案的运行情况吧!
有必要解释下,我们使用0和1分别代表可以不能通过和能够通过,千万不要和当前的步数混淆哈!
转:http://www.cnblogs.com/JackyTecblog/archive/2011/02/20/1958880.html