.NET C#教程初级篇 11 基本数据类型及其存储方式

.NET C# 教程初级篇 1-1 基本数据类型及其存储方式

本文目录

• 1. 全文目录
• 2. 基础数据类型介绍
• 3. C#中两种数据存储方式
  • 3.1 堆栈
  • 3.2 托管堆
• 4. 常见的几种数据类型
• 5. 数据的存储方式
  • 5.1 进制
  • 5.2 正负数存储形式及四种码
  • 5.3 定点数与浮点数存储方式
  • 5.4 数据的存储方式（选看）
  • 5.5 值与引用类型的存储方式
• 6. C#中定义变量的方式及数据转换的方法
• 7. 数组
• 8. 运算符及规则重载
  • 8.1 基础的运算符
  • 8.2 运算符的重载
• 9. 结构体(选看)
• 10. 练习题
  • 10.1 理论分析题
  • 10.2 计算题
  • 10.3 编程题
• 11. Reference
• 12. About Me

全文目录

（博客园）.NET Core Guide

（Github）.NET Core Guide

本节内容是对于C#基础类型的存储方式以及C#基础类型的理论介绍

基础数据类型介绍

例如以下这句话：“张三是一名程序员，今年15岁重50.3kg，他的代号是‘A’，他家的经纬度是(N30,E134)。”，这句话就是一个字符串，使用双引号括起来。而15则表示是一个 整数类型，50.3就是小数类型，不过我们在C# 中通常称为 浮点类型，最后一个经纬度，我们通常定位地点的时候都是成对出现，所以我们认为这二者是一个密不可分的结构，这种类型我们称为 结构体类型(struct)。

以上我所说的数据类型都是一个所含有信息量一定的数值，我们称为值类型；而张三这个人，他所含有的数据大小是不固定的，比如我又了解到了张三是一个富二代，那么他就会增加一个属性是富二代，我们需要更多的空间去存储他，张三这个变量我们通常就称为引用类型，而张三这个名字，我们就称为引用，如果你对C或者C++熟悉的话，张三这个名字就是指向张三这个人（对象）的一个指针。

C# 中两种数据存储方式

在C# 中，数据在内存中的存储方式主要分为在堆中存储和栈中存储。我们之前提到的值类型就是存储在栈中，引用类型的数据是存储在堆中，而数据是在栈中。

值类型：存储在栈(Stack，一段连续的内存块)中，存储遵循先进后出，有严格的顺序读取访问速度快，可通过地址推算访问同一个栈的其余变量。

引用类型：引用(本质上和C++中的指针一致)存储在栈中，内含的数据存储在堆中(一大块内存地址，内部变量存储不一定连续存储)。

事实上，值类型和引用类型有一个很明显的区别就是值类型应当都是有值的，而引用类型是可以为空值的。在C#中，内存管理相比于C/C++是更加安全的，在C/C++中我们可以自由的申请和释放内存空间，C#采用堆栈和托管堆进行内存管理。也就是绝大部分的内存管理都交给了CLR。通常来说栈负责保存我们的代码执行（或调用）路径（也就是直接指向的数据的内存地址）,而堆则负责保存对象（或者说数据，接下来将谈到很多关于堆的问题）的路径。

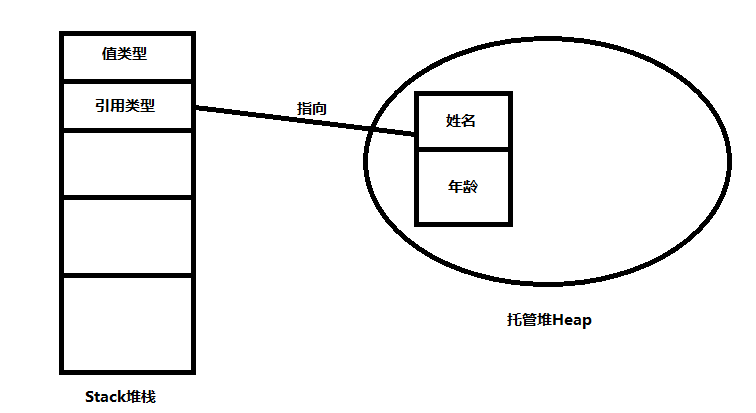
考虑到实际难度，在这里我们不做太多深入的研究，具体的分析内容读者可以查看本教程的番外补充篇进行学习。

堆栈

堆栈一般用于存储数据引用（指针）或是一些值类型，它的空间并不大，通常只有几M大小，它的读取速度是快于存储在堆中的数据的。

托管堆

在C#中微软使用了托管堆进行内存的管理，引用类型的实例是内存释放都交给了GC（垃圾回收器）进行自动的处理。这样保证了内存的安全性。下图是垃圾回收的机制：

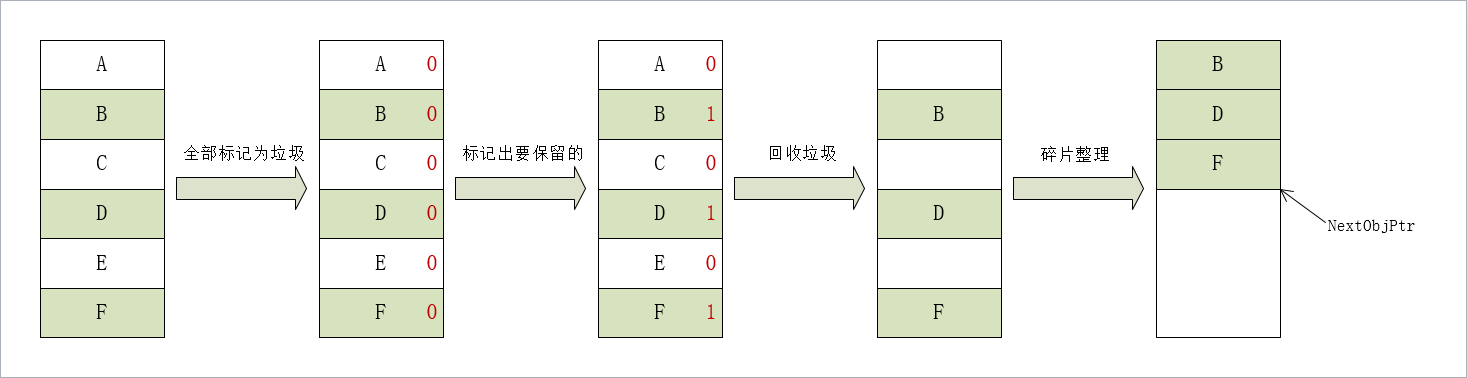
常见的几种数据类型

• 字符类型：char字符类型，代表无符号的16位整数，对应的可能值是ASCⅡ码,你可以上网搜索ASCⅡ码的内容
• 整数类型：常用的一般有：byte，short，int，long。各代表8位、16位、32位、64位整型。占用内存分别为（位数/8）字节。范围则是 +-(位数)个1组成的二进制的十进制数/2。例如byte的范围则是11111111转十进制后除以2取反，即-127~128。范围绝对值之和为256。
• 浮点类型：float, double, decimal：浮点类型，分别代表32位、64位、128位浮点类型。通常默认类型是double，如果需要指定float类型，需要1.3f，decimal类型则指定1.3m。浮点型存在的问题是精度的损失，并不一定安全。
• 布尔类型：bool类型是一个二进制中的0和1，各代表了false和true。只存在两个值。
• 字符串类型：string本质是一种语法糖，作为字符类型的数组引用(指针)存在，也是String类的简写
• 委托类型：delegate用于绑定函数，为引用类型的一种，将函数参数化为变量。本质上就是C++中的函数指针。
• 数组：继承自Array类，属于任意类型的一种集合，但不同于集合，大小必须被初始化。在内存中是一段连续的内存空间，但是不是值类型。

数据的存储方式

对于大部分学习者而言，数据的存储方式是一个相对陌生的概念，但是为了全面理解和学习，还是有必要进行一个简单的学习的。这里不会讲述过难的组成原理知识，只是让读者明白一些有关计算机科学的原理和常识。

进制

首先我们学习一下在计算机常用的一些进制，这里以二进制、八进制和十六进制进行展开。在进行讲解之前，提出一个问题，为什么我们的计算机都是以二进制为基础进行算数的运算呢？

其实答案很简单，因为计算机是采用数字电路进行逻辑运算最终实现我们的功能的，而对于一条电路而言，它的电位只有高低两种电平，或者理解为只分为有电流和无电流通过。因此使用0和1作为标识是非常实用的。同时采用二进制也有利于我们电路逻辑的设计。

二进制的运算非常的简单，从低到高位分别赋予权重\(2^{n-1}\)，n为位数，而一串二进制的十进制表示的计算公式为

\[\sum_{i=0}^{-m}K_i*2^i \]

其中\(K_i\)称为位权，取值是0或1，更一般的，一个r进制数的的位权取值是一个大于0小于r-1的数，r进制数转换为10进制的计算公式如下：

\[\sum_{i=0}^{-m}K_i*r^i \]

在C#中，表示一个二进制通常用Ob开头，8进制则是以0开头，16进制以0x开头，例如

int a = 0b101011;//二进制
int b = 035167;//八进制
int a = 0xD2F3;//十六进制

讲完了二进制数，接下来我们讲讲八进制和十六进制。既然二进制如此美妙好用，为什么各位计算机学家还是要在计算机大量的使用八进制和十六进制呢？一个很明显的例子就是变量在内存中往往都是以8或16进制进行存储，不知道你有没有看过时常弹出来的错误窗口中会提示内存0xfffff错误，这里就是使用了我们的十六进制。原因是因为一段过长的二进制值是可读性非常差的，而选择八进制和十六进制正是缩短了过长的二进制，因为八进制逢8进1，也就是2的3次方，十六进制则是2的4次方，十六进制超过9以后的数以字母A~F表示。例如101011011011这串二进制代码，如果换算成八进制则是05333，转换成为十六进制则是0xACB，很明显大大缩小了我们的阅读难度，同时因为其是2的整数次方，转换也十分的简单迅速。

二进制转八进制的诀窍是，从低到高位，每三位一组（\(2^3\))，最后不足三位的前面添0，以每一组二进制的值为位权，最终就是我们的八进制数。十六进制也一样，只不过改成以4个为一组（\(2^4\))。如果将16或8进制转换成为2进制，则将十六或八进制中从每一位按4或3位展开即可。例如

1011011011转八进制的过程，先添0补足长度为3的倍数，001011011011，分组001|011|011|011，则表示为1333，十六进制和N进制转2进制希望读者自己尝试解决。

如果带小数点，则依次类推，只不过我们指数幂就换成负数即可，这里不再展开赘述。

在C#中也提供了相关的函数方便我们迅速进行进制间的转换

// value为需转换的R进制数，以字符串表示，fromBase为需转换的进制
Convert.ToInt32(string value, int fromBase)：

// value为需转换的十进制数，toBase为需转换的进制
Convert.ToString(int value, int toBase);

值得补充的一点是，数据在内存中的存储大小本身是由数据的 位（bit） 决定的，我们常说的一字节在现在的计算机中指有8个比特空间大小，一个比特位可以存储一位二进制代码，而我们常见的int类型默认是Int32，也就是32位整形，因此你知道为什么int是4个字节了吧？

正负数存储形式及四种码

在计算机中，数据往往并不是直接以数值本身的二进制码（机器数）进行存储和计算的，我们往往需要对数值的二进制码进行一些变换。同时你是否想过，正数我们可以直接写出它的二进制码，那么碰到负数我们又应该如何做呢？也许聪明的你已经想要脱口而出：既然因为电位只有两种状态我们用0和1进行表示，正负也只有两种表示方法！因此我们在二进制码的头部增加一位符号位进行有符号数的正负标识，这里我们用1表示负号，0表示正号。这里似乎又解决了我们一个很头大的问题：为什么int、long这种有符号数表示的范围是要比它所占的位数少一位，因为最高位用于标识它的符号了。

这里我们引入下一个概念 “原码”：原码是最简单、直观的机器数表示方法了，也就是用机器数的最高位标识它的符号，其余为数据位是数的绝对值。例如-8这个十进制数用二进制原码表示就是1100。值得一提的是，0在原码表示法中有两种表示，+0和-0。

反码 ：反码的概念非常的简单，通常反码在计算机中只起到原码到补码转换的过渡过程。在这直接抛出计算方法而不做赘述。对于正数，反码就是其本身，对于负数，反码则是将原码中除符号位外每一位数字进行逻辑取反，因此它的性质和原码其实是一致的。 例如+8的二进制为0,100，反码就是0,100，对于-8的二进制1,100，反码则为1,011

接下来介绍的是计算机中真正的数据存储方式，补码：首先，补码正如其名，和原码是一对互补的数字。它的和原码之间的关系是：对于正数，补码就是其本身，对于负数，原码的反码+1=补码。

我们引入一个生活中的小例子，我们在看钟表的时候，如果以0（12）作为基准，如果现在指针指向3，我们正常会以顺时针从0（12）开始数到3，得知现在是3点，如果是指向9，我们则会从0（12）开始逆时针开始数。或者说，你看到15点会不自觉的知道指针指向3，因为15-12=3，这里其实就已经用到了补码的概念。事实上，在计算机的结构中，加法是可以直接进行运算的，但是并没有针对减法设计数字电路，因为减法的数字电路并不容易设计，同时也出于节约成本的考虑，如果只设计加法电路的情况，如何去得到我们的减法？这里先需要知道一个运算求余——%，例如7%3=1，即除法后的余数。我们就以7-3为例子，试着将一个减法运算成加法。

答案非常的显而易见，7-3不就是7+(-3)吗？你可以假设一个钟表，它的最大值是12，现在指向7，我们定义顺时针为正，逆时针为负。现在钟表指向了7，我们逆时针往回转3个小时，指针指向了4。那么问题来了，我们是不是也可以顺时针转9格也得到4呢？按着我们的定义7+9=16并不等于4，但我们的钟表最大也只有12呀，因此我们需要将溢出位丢弃，也就是取余操作(7+9) mod 12=4。这样我们就成功的将一个减法运算设计成了加法运算了。

因此回到我们补码的概念，那么7-3实际上是7和-3进行相加，加法是可以直接运算的，而从补码和反码的定义我们知道负数的反码是数值位进行取反而符号位不变，因此负数的\([反码+原码+1]_原=最大值+1\)也就是\([补码+原码]_原=最大值+1\)，这也就体现了补码的名称了。因此对于减法\(x-y(x>0,y>0)\)，可以化为\((x+[y]_补)\%(max+1)\)，其实证明并不难，如下

\[\forall x>0,\forall y>0;\\ y_补=max-y_原+1\\ x+y_补 = x-y_原+max+1\\ 因此很显然x-y = x+y_补=(x-y_原+max+1)\%(max+1)得证 \\\]

更一般的，若数据表示的最大原码为M-1，对于定点类型数（整数、定点小数），有

\[[A+B]_补 = （A_补+B_补）mod M \\ \\ [A-B]_补 = （A_补+[-B]_补）mod M \]

讲到这里，其实也就解释通了为什么在计算机中，数据都是以补码的形式进行存储和运算了，因为可以讲任意的加减法（乘除法实际上也就是循环型的加减）都按着加法进行运算，有利于节省成本和降低设计难度。

移码是我们四码里面的最后一种码，它通常用于表示浮点数的阶码，具体的运用在下文会详细的进行介绍，这里不再展开。移码的定义非常简单，就是在真值X上加上偏置量，通常是以2的n次方为偏置量，就相当于X在数轴之上偏移了若干个单位。移码的求解方法非常简单，将补码的符号位取反就是移码。例如真值1，进行移位\(2^4\)得到了17,转换成为补码形式就是10001。

定点数与浮点数存储方式

定点数和浮点数统称实型，点指代小数点，定点数无需解释，我们只要事先规定好整数位和小数位的数量即可表示。对于浮点数，

*数据的存储方式（选看）

数据的存储方式主要分为大端存储和小端存储、边界对齐存储（详情请看结构体的内容）两种。对于现代的计算机，数据的存储通常以字节编址，也就是一个地址编号对应的内存单元存储1个字节。那么对于一个大的数据，我们可能会存储在连续的多个内存单元之中。

大端小端没有谁优谁劣，各自优势便是对方劣势，我们不太需要关注哪一种存储方式，只需要大体了解一下即可。

• 小端存储就是低位字节排放在内存的低地址端，高位字节排放在内存的高地址端。
• 大端存储就是高位字节排放在内存的低地址端，低位字节排放在内存的高地址端。

例如数字0x12345678进行存储时，存储内存结构如下图。

小端模存储中强制转换数据不需要调整字节内容，1、2、4字节的存储方式一样。而在大端存储中符号位的判定固定为第一个字节，容易判断正负。

为什么要学这个奇怪的知识呢？因为在跨语言或平台的通信之中，不了解这个知识总是会有一些奇奇怪怪的错误出现，例如Java网络通信中，数据流是按大端字节序，和网络字节序一致的方法进行传输，而C#在Windows平台上是小端字节序进行数据存储。那么如果一个Java程序往一个C#程序发送网络数据包的时候，由于数据存储顺序的不同就会导致数据读取结果的不同。

大家可以阅读这两篇博文进行一个理解：

• 大端和小端存储模式详解
• C# 大端与小端（因为大小端引起的奇怪问题）

值与引用类型的存储方式

在前文中我们其实已经讲过许多有关值类型和引用类型的存储，大体上我们值类型、指令、指针等是直接存储在栈中，而引用类型、委托等指针指向的类型则存储在托管堆中。具体请看文章开头处对数据类型的简介。

C#中定义变量的方式及数据转换的方法

在C#中定义变量的方式和其他的主流语言没有太大的区别，以下是几种定义方式:

int number = 5;//定义一个32位整数类型
bool b = true;//定义
//注意看以下两条，string定义的字符串必须为双引号，而char使用单引号并且只允许输入一个字符
string str = "test";
char a = 'a';
//记得后缀
float f = 1.3f;
decimal d = 1.5m;

数据类型的转换分为隐式转换和显式转换，看下面几个例子：

string a = "15";
int b = int.Parse(a);//显式转换
b = (int)a;//强制转换
b = Convert.ToInt32(a);//显式转换，较常用
double d = 1.5;
b = d;//隐式转换

如果我们定义的数据大小超过了数据类型本身的大小，那么位于高位的数据会被首先舍弃。

这里还有一种相对特殊的类型——无符号类型，通过前文的介绍，我们大体已经知道了有符号数字的定义以及存储方式，而对于无符号数，补码原码反码都是其本身，也就是将首位的符号位替换成了数据位。当有符号数向无符号数进行转换时，我们需要计算出有符号数的补码，然后直接按公式进行计算。例如:

int a = -3;//补码为100
uint b = a;//b=8

数组

数组指一个类型（任意）的集合，例如你定义一个变量为a=5，很轻松，假设你需要100个呢？因此我们使用数组来存储。
数组的定义以及使用如下：

//伪代码，T为类型，n为大小
T [] t = new T[n]；
//定义一个整型数组
int [] a = new int [5];
//你也可以选择初始化的方式定义
int [] b = new int [] {1,2,3,4,5};
//或
int [] c = new int [5]{1,2,3,4,5};
//数组的访问，从0开始索引
Console.WriteLine(b[0]);

有时候我们也许会想用一个表格进行数据的存储，例如我们存储一个矩阵就需要二维的空间，这里给出二维数组的定义：

//伪代码，T为类型，m,n为大小
T [,] t = new T[m,n]；

本质上二维数组的概念就是数组的数组，一个组成元素为一维数组的数组就是我们的二维数组。一般而言，我们需要指定二维数组的行列宽，当然我们也可以不指定行数直接初始化，但我们必须指定列数，因为内存是按行进行分配。

运算符及规则重载

基础的运算符

• +-*/：对应数学中的加减乘除。
• %： 求余运算，a%b指a除以b的余数。
• & | ~ ^ ：分别为按位与、按位或、按位取反、按位异或
• <<、>>：左右移位运算符,例如0010 --> 0100
• ？：三元判断运算符

^是异或,result=1110,就是说异是不同返回1，相同是0，或就是只要有1就返回1。

&是与, result=0001,也就是相同返回1，不同为0

|是或, result=1111,除了两个都为0，否则返回1

~称为按位取反，我们表示符号是用四个0表示，运算规则就是正数的反码，补码都是其本身的源码，
负数的反码是符号位不变，本身的0变1,1变0，补码就是反码+1，
最后进行补码取反时连同符号位一起变得到的反码就是结果
流程如下：0000 0111 --> 0000 1000 --> 0000 1001 --> 1111 0110 = -8

>>称为右移,右移一位流程如下 0000 1001 --> 0000 0100 = 4

<< 称为左移,左移一位流程如下 0000 1001 --> 0000 10010 = 18

移位运算需要注意的一点是，由于我们计算机保存数据的方式是采取补码存储，因此，当我们对一个负数进行移位时，在添加的并不是0而是1。

运算符的重载

我们在大部分时候，语言自身提供的运算符运算规则已经足够我们使用，但往往我们会涉及到一些奇怪的场景，例如我需要知道某两个节日的日期相距多少天而我并不想借助DateTime类的方法，我想用date1-date2进行计算，那么我们就需要使用运算符重载去改写减号的规则。

事实上我们仔细思考不难得出结论，一切的运算符本质上都是一种函数的对应关系，那么我们使用operator关键字进行某类中运算符的重载，例如：

// T是修改类型的返回值
public static T operator +(D d1,D d2)
{
    return something;
}

通过运算符重载，我们可以更有效的书写高质量的代码，同时可读性也可以大大提升。

具体的操作我会在我在BiliBili上发布的 .Net Core 教程上进行详细的讲述。

*结构体(选看)

结构体是一种比较特殊的数据类型，它很像我们后面讲述到的类，但是他并不是一个类，他本质还是值类型，结构体的使用是很重要的，如果结构体使用得当，可以有效的提升程序的效率。

结构体你可以理解为将将若干个类型拼接在一起，但是存在一个很重要的内容——内存对齐。例如下面两个结构体：

struct S
{
    int a;
    long b;
    int c;
}
struct SS
{
    int a;
    int b;
    long c;
}

乍一看你会觉得这两个结构体完全一致，丝毫没有任何的差别。但事实上，在大多数编程语言里面，对于结构体这种大小并不是定值的值类型，都存在一个最小分配单元用于结构体内单个变量的大小分配。在内存中，他们两个的存储方式有很大的不同。
对于上面两个结构体，他们在内存中的单元分配是：

• S：a(4 byte + 4 free) --> b(8 byte) --> c(4 byte + 4 free)，共计24字节
• SS：a(4 byte)b(4 byte) --> c(8 byte)，共计16字节

在C#中，如果你不指定最小分配单元，那么编译器将会把结构体中占用内存最大的作为最小分配单元。不过尤其需要注意一件事，就是引用类型在结构体中。鉴于我们现在尚未讲解面向对象的类，我们用string作为成员写一个结构体。如下面这个例子：

struct S
{
    char a;
    long b;
    string c;
}
//函数中创建
S s = new S();
s.a = 'a';
s.b = 15;
s.c = "I Love .NET Core And Microsoft"

很显然s.c的大小超过了结构体中其余两个，但是内存分配的时候就是以最大的c作为标准吗？

显然不是，我们要知道struct是在栈中分配内存，string的内容是在堆中的，所以在结构体中存储的string只是一个引用，并不会包含其他的东西，只占用4个字节。并且特别的，引用类型在内存中的位置位于大于四字节的字段前，小于四字节字段后。

上面内存分配应当是这样：
a(8) --> c(8) --> b(8)。

如果需要深入了解这一方面内容，建议去阅读《CLR Via C#》这本书，以及学习SOS调试相关内容。

10. 练习题

理论分析题

• 计算出int和long的数值范围
• 为什么在大部分提供科学计算或编程语言会存在精度问题？例如浮点数2.5在任何一种采用二进制计算的编程语言中也不是一个精确值？或者说如果我们展开浮点数的所有精确位，最后的几位小数并不是0？（较难）
• 为什么引用类型即使不存储内容也需要内存空间？
• 试说明引用类型和值类型的优缺点
• 数组为什么需要初始化大小？如果是多维数组，不指定列宽可以吗？

计算题

• 求123.6875的二进制、八进制、十六进制表达式。
• 求\((11011.101)_2\)二进制小数转换为十进制。
• a=5，b=8，试手算a&b，a|b，a^b，a<<1， b>>1
• 若a=12，试手算~a
• 若a为8位二进制，试着写出将a的高四位取反，第四位不变的运算表达式
• int a = 15，试求a+int.MaxValue的值

编程题

• 请学习指针内容以及C#unsafe调试，试着不使用索引进行数组的读取。
• 将字符串”15”转成整数？
• 使用运算符重载，计算向量的加减和点乘（内积）

Reference

《C# in Depth》—— Jon Skeet

《计算机组成原理》——唐朔飞

C#托管堆和垃圾回收（GC）

C# Heap(ing) Vs Stack(ing) In .NET

大端和小端存储模式详解

C# 大端与小端（因为大小端引起的奇怪问题）

About Me

作　　者：WarrenRyan
出　　处：https://www.cnblogs.com/WarrenRyan/
本文对应视频：BiliBili(待重录)
关于作者：热爱数学、热爱机器学习，喜欢弹钢琴的不知名小菜鸡。
版权声明：本文版权归作者所有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文链接。若需商用，则必须联系作者获得授权。
特此声明：所有评论和私信都会在第一时间回复。也欢迎园子的大大们指正错误，共同进步。或者直接私信我
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是作者坚持原创和持续写作的最大动力！


博主一些其他平台：
微信公众号：寤言不寐
BiBili——小陈的学习记录
Github——StevenEco
BiBili——记录学习的小陈（计算机考研纪实）
掘金——小陈的学习记录
知乎——小陈的学习记录

联系方式

电子邮件：cxtionch@live.com

社交媒体联系二维码：