1.基本概念:
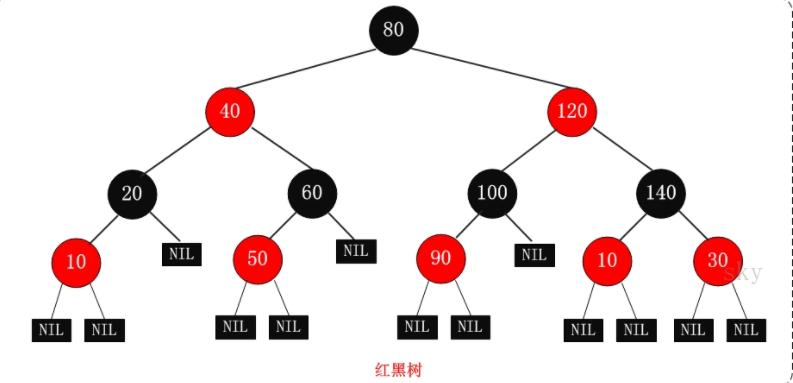
红黑树,一种二叉查找树,但在每个节点上增加一个存储位表示节点的颜色,红色或者黑色,通过对任何一条从根到叶子的路径上各个节点着色方式的限制,红黑树确保没有一条路径会比其他路径长处两倍,因而接近是平衡的。
2.特性:
(1)红黑树是一颗二叉查找树,执行查找,插入,删除等操作的时间复杂度为O(lgn)
(2)如果一颗具有n个节点的线性链,那么二叉查找树的最坏情况时间O(n),而红黑树能保证在最坏情况下,基本的动态几何操作的时间均为O(lgn)。
红黑树的特点:
1).每个节点要么是红的,要么是黑的。
2).根节点时黑的。
3).每个叶子节点,即空节点(NIL)是黑的。
4).如果一个节点时红的,那么它的两个儿子都是黑的。
5).对每个节点,从该节点到其子孙节点的所有路径上包含相同数目的黑节点。
3.树的旋转
前景:当我们对红黑树进行插入和删除等操作时,对树做了修改,可能会违背红黑树的性质,为了保持红黑树的性质,我们可以通过对树进行旋转,即修改树种某些节点的颜色及指针结构,以达到红黑树进行插入,删除等操作,红黑树依然能保持它特有的性质。
3.1 左旋:
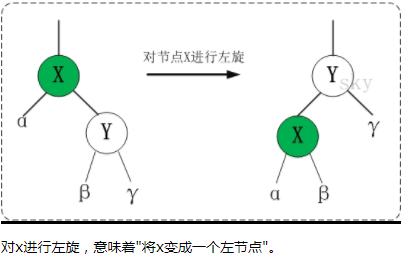
1).如果x的父节点是空节点,则将y设为根节点;
2).如果x是它父节点的左孩子,则将y设为“x的父节点的左孩子”;
3).如果x是它父节点的右孩子,将y设为“x的父节点的右孩子”;
将x设为y的左孩子,
将x的父节点设为y
3.2右旋

对Y进行右旋,意味着“将Y变成一个右节点”
如果“y的父亲”是一个空节点,则将X设为根节点;
如果y是它父节点的右孩子,则将x设为“y的父节点的右孩子”
如果y是它父节点的左孩子,将x设为“y的父节点的左孩子”
将y设为x的右孩子,
将y的父节点设为x
原文参考:http://www.cnblogs.com/v-July-v/archive/2010/12/29/1983707.html
http://www.cnblogs.com/skywang12345/p/3245399.html