分治法:将问题分解,通过求解局部性的小问题来解开原本的问题
递归:自己调用自己,我们见的比较多的递归的例子就是斐波那契数列求解问题。
分治法和递归经常在一起使用。
分治法:
- 将问题“分割”成局部问题
- 递归地求解局部问题
- 将局部问题的解“整合”,解决原问题
穷举搜索
题目链接: http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_5_A
Write a program which reads a sequence (A) of (n) elements and an integer (M), and outputs "yes" if you can make (M) by adding elements in (A), otherwise "no". You can use an element only once.
You are given the sequence (A) and (q) questions where each question contains (M_i).
Input
In the first line (n) is given. In the second line, (n) integers are given. In the third line (q) is given. Then, in the fourth line, (q) integers ((M_i)) are given.
Output
For each question (M_i), print yes or no.
Constraints
- n ≤ 20
- q ≤ 200
- 1 ≤ elements in A ≤ 2000
- 1 ≤ (M_i) ≤ 2000
Sample Input 1
5
1 5 7 10 21
8
2 4 17 8 22 21 100 35
Sample Output 1
no
no
yes
yes
yes
yes
no
no
Notes
You can solve this problem by a Burte Force approach. Suppose solve(p, t) is a function which checkes whether you can make t by selecting elements after p-th element (inclusive). Then you can recursively call the following functions:
solve(0, M)
solve(1, M-{sum created from elements before 1st element})
solve(2, M-{sum created from elements before 2nd element})
...The recursive function has two choices: you selected p-th element and not. So, you can check solve(p+1, t-A[p]) and solve(p+1, t) in solve(p, t) to check the all combinations.
For example, the following figure shows that 8 can be made by A[0] + A[2].
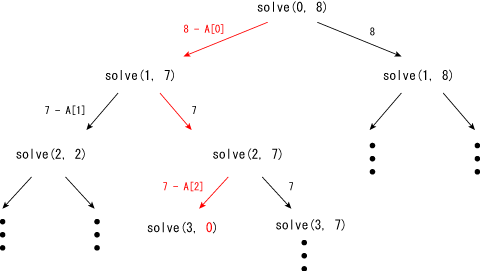
题目的数据量较小,我们可以列举出所有的组合。每个元素有“选”或“不选”两种情况,所有一共有(2^n)种组合。
参考代码如下:
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class ExhaustiveSearch {
static int n;
static int[] num;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = Integer.parseInt(br.readLine());
String[] strs = br.readLine().split("\s+");
num = new int[n];
for (int i=0; i<n; i++){
num[i] = Integer.parseInt(strs[i]);
}
int q = Integer.parseInt(br.readLine());
strs = br.readLine().split("\s+");
for (int i=0; i<q; i++){
if (solve(0, Integer.parseInt(strs[i]))){
System.out.println("yes");
}
else {
System.out.println("no");
}
}
}
private static boolean solve(int i, int m) {
if (m == 0){
return true;
}
if (i >= n){
return false;
}
// 关键步骤
boolean res = solve(i+1, m) || solve(i+1, m-num[i]);
return res;
}
}
参考文献:《挑战程序设计竞赛-算法和数据结构》