Dijkstra算法主要是针对单源的,用于求一个点到其他各点的最短路径。其中点与点之间的边的权重不存在负值的情况。
先看下图(手上没有好的画图工具,先将就看看):
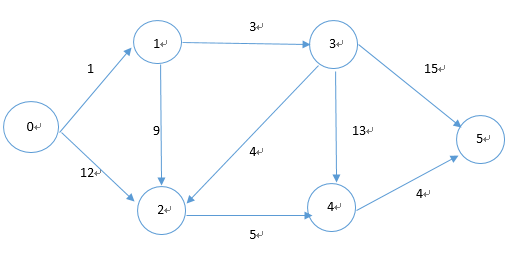
设以点0位源点,求0到其他各点的最短路径。
首先我们用一个二维矩阵来表示各点之间的距离(这个矩阵太丑了):
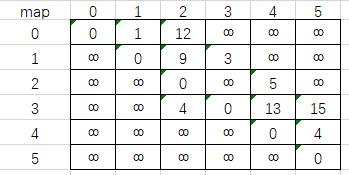
这个二维矩阵表示的只是各点之间的距离。所以我们为了能够更直观的看出源点到其他各点的距离,可以用一个一维数组去记录源点到其他各点的距离:

其中的dis[i]代表源点到点i的直接可达距离。
准备工作完成之后,我们可以进行求解了:
首先找到距离源点最近的点,通过dis这个数组可以得到,1号顶点是距离源点最近的点。当选择了1号顶点之后,那么dis[1]的值就完全确定了,原因是这个图的所有边的值都是正数,而源点到1号顶点的距离是最近的,所以源点到1号顶点的距离不可能通过第三个顶点中转,使得源点到1号的距离进一步缩短。
在选择了1号顶点之后,可以看1号的出边有哪些。通过图可以看到,1号的出边有1→2以及1→3两条边。我们首先讨论一下1→2这条边。现在,我们可以比较,究竟是0→2的距离短还是0→1→2的距离短,其中0→1→2的距离可以通过dis[1]+dis[1][2]来计算。可以发现,0→1→2的距离为1+9=10,而0→2的距离为12,所以从源点到2号顶点的暂时的最近距离为10,故我们可以更新dis数组:

再来讨论0→3的距离:
在dis数组中可以发现,源点到3号顶点是没有直接路径可以到达的,但是可以通过0→1→3这条路径抵达,那么0→3目前的最短距离即为dis[1]+map[1][3]=4,所以我们可以再次更新dis数组:

同理,源点到其他各点的距离,可以通过上面的步骤来求得,最终的结果如下:

现在,我们可以总结一下Dijkstra算法的思想了:每次找到距离源点最近的一个顶点,然后以该顶点为中心进行扩展,最终得到源点到其他各点的最短路径。基本步骤如下:
①首先把所有的顶点分为两个部分:已找到最短路径的顶点集合P和未找到最短路径的顶点集合Q。最开始进行时,P中只有源点这么一个元素。在这里,我们可以用一个标记数组visited来记录哪些点在集合P中;
②设一个数组dis来存储源点到其余各点之间的距离,那么dis[0]=0。如果存在有源点可以直接到达的顶点i,那么把dis[i]设为map[0][i],其余的各点设为无穷大;
③在Q中选择一个距离源点最近的顶点u(dis[u]最小),加入到集合P中。同时以u为中心点,向周围扩展,考察所有以u为起点的边,并且进行松弛操作。需要的话,可以及时更新dis数组中的值。
④重读第③步,当Q为空时,代表源点到其他各点的最短路径均已找到,算法结束。
实现代码如下:
import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); int N = sc.nextInt(); //顶点的个数 int M = sc.nextInt(); //边的个数 int max = Integer.MAX_VALUE; //无穷大,设为不可达 int[][] map = new int[N][N]; //存储各顶点之间的距离 for (int i = 0; i < N; i++){ for (int j = 0; j < N; j++){ if (i == j) map[i][j] = 0; else map[i][j] = max; } } //输入各点之间的距离 for (int k = 0; k < M; k++){ int a = sc.nextInt(); //起点 int b = sc.nextInt(); //终点 int c = sc.nextInt(); //距离 map[a][b] = c; } int[] dis = new int[N]; //源点到各点的距离,源点设为0 for (int i = 0; i < N; i++) dis[i] = map[0][i]; boolean[] visited = new boolean[N]; visited[0] = true; //Dijkstra for (int i = 0; i < N; i++){ int min = max; int idx = 0; //找到距离源点最近的点 for (int j = 0; j < N; j++){ if (!visited[j] && dis[j] < min){ min = dis[j]; idx = j; } } visited[idx] = true; //扩展 for (int k = 0; k < N; k++){ if (map[idx][k] < max){ if (map[idx][k] + dis[idx] < dis[k]) dis[k] = map[idx][k] + dis[idx]; } } } for (int l = 0; l < N; l++){ System.out.print(dis[l] + " "); } } }
输入数据及输出结果:
