浅谈RMQ实现LCA

求两个点的LCA一共有四种方法

Tarjan，倍增，RMQ还有树链剖分（我也不会）

今天我们来学习如何用RMQ来实现LCA

首先我们要知道什么是RMQ（区间最值）

推荐一篇大佬的博客:https://www.cnblogs.com/YSFAC/p/7189571.html

好了，现在大家都知道了什么是RMQ，那么我们来看一下什么是LCA

LCA是树上两个点的最近公共祖先

举个例子：

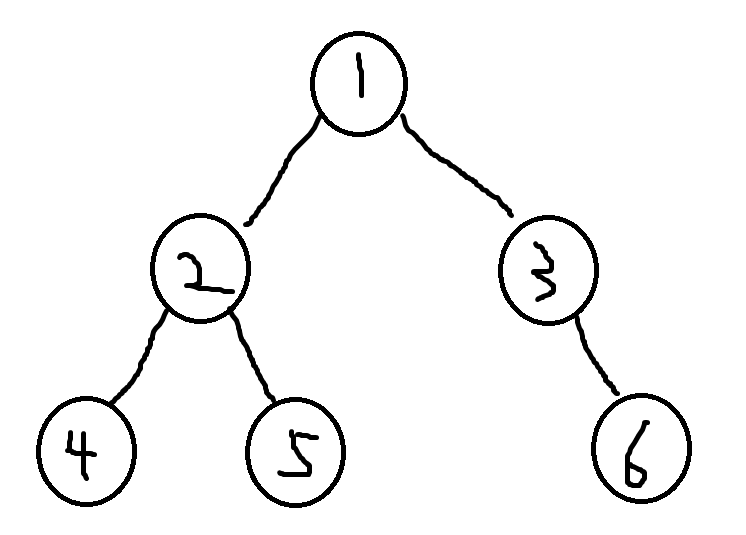
在这个图中，4和5的最近公共祖先就是2

5和6的最近公共祖先就是1

然后我们来看如何快速的求出两个点的最近公共祖先

首先是求出每个点的深度

这个操作用一个DFS维护即可，每个店的深度是其父亲的深度加1

void dfs(int x,int fa){
    for(int e=head[x];e;e=nxt[e]){
        d[to[e]]=d[x]+1;
        dfs(to[e],x);
    }
    return ;
}

然后是维护f数组

f数组储存的是每个点向上跳2^j步所到达的点，并且我们可以确定这个点是唯一的，因为是树

然后来看如何维护

我们可以用递推的方法来求，时间复杂度是(nlogn)的

对于f[i][j]

是从x往上跳2^j步

可以推导出相当于是从x往上跳2^j-1步，然后再跳2^j-1步

也就是相当于从x往上跳2^j-1步之后，从那个点在往上跳2^j-1步

由此得出了我们的递推式:

f[i][j]=f[f[i][j-1][j-1]

实现起来也就很简单了，f[i][0]已经在DFS里处理过了

void pre(){for(int j=1;j<=17;j++) for(int i=1;i<=n;i++) f[i][j]=f[f[i][j-1]][j-1];}

最后就到了最重要的一步

求两个点的LCA

时间复杂度大约为logn，其实也可以当做O(1)

step1：

将两个点跳到同一高度

为了代码简洁

我们确保x的深度较深

往上跳的条件是跳完之后的深度小于等于y的深度

（因为要确保跳完之后深度一样）

于是代码也就好写了

step2：
两个点一起往上跳

我们的目标是将两个点跳到他们最近公共祖先的两个子节点处

 为啥不直接跳上去呢

因为我们的判断条件是两个点跳完之后不相同才可以跳，否则会直接跳到根节点

现在我们的代码已经呼之欲出了

下面给出代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<cstdlib>
#include<string>
using namespace std;
inline int rd(){
    int x=0,f=1;
    char ch=getchar();
    for(;!isdigit(ch);ch=getchar()) if(ch=='-') f=-1;
    for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
    return x*f;
}
inline void write(int x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
    return ;
}
int n,m,root;
int total=0,head[1000006],to[1000006];
int nxt[1000006];
int f[1000006][20];
int dep[1000006];
inline void add(int x,int y){
    total++;
    to[total]=y;
    nxt[total]=head[x];
    head[x]=total;
    return ;
}
inline void dfs(int x,int fa){
    f[x][0]=fa;
    for(int e=head[x];e;e=nxt[e]){
        if(to[e]==fa) continue;
        dep[to[e]]=dep[x]+1;
        dfs(to[e],x);
    }
    return ;
}
inline void pre(){for(int i=1;i<=18;i++) for(int j=1;j<=n;j++) f[j][i]=f[f[j][i-1]][i-1];}//预处理出每个点往上跳2^j步会到哪里 
inline int lca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=17;i>=0;i--) if(dep[f[x][i]]>=dep[y]) x=f[x][i];
    if(x==y) return x;
    for(int i=17;i>=0;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];
    return f[x][0];//因为是到了最近公共祖先的两个子节点，所以还要再往上跳一步 
}
int main(){
    n=rd(),m=rd(),root=rd();
    for(int i=1;i<n;i++){
        int x=rd(),y=rd();
        add(x,y),add(y,x);
    }
    dep[root]=1;
    dfs(root,0);
    pre();
    for(int i=1;i<=m;i++){
        int x=rd(),y=rd();
        write(lca(x,y)),puts("");
    }
    return 0;
}