借鉴:http://blog.kongfy.com/2015/02/kargermincut/
提到无向图的最小割问题,首先想到的就是Ford-Fulkerson算法解s-t最小割,通过Edmonds–Karp实现可以在O(nm2)时间内解决这个问题(n为图中的顶点数,m为图中的边数)。
但是全局最小割和s-t最小割不同,并没有给定的指定的源点s和汇点t,如果通过Ford-Fulkerson算法来解这一问题,则需要枚举汇点t(共n−1),时间复杂度为O(n2m2)。
Can we do better?
答案是肯定的,Karger在攻读博士学位期间(Orz…)提出了非常著名的基于随机化的全局最小割算法,算法非常简单,简单到不敢相信它是正确的,算法描述如下:
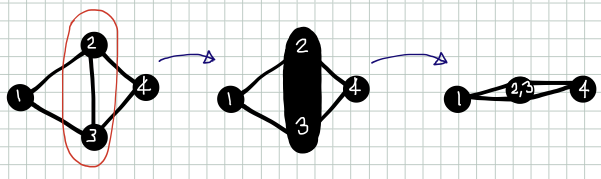
- 在图中随机取一条边,将边的两个端点合并(contraction),同时消除所有由于合并而形成自环的边
- 重复步骤1直到图中仅剩下两个点
- 将最终两点之间的边作为找的割返回
合并的边权值相加
1.min=MAXINT,固定一个顶点P
2.从点P用“类似”prim的s算法扩展出“最大生成树”,记录最后扩展的顶点和最后扩展的边
3.计算最后扩展到的顶点的切割值(即与此顶点相连的所有边权和),若比min小更新min
4.合并最后扩展的那条边的两个端点为一个顶点(当然他们的边也要合并,这个好理解吧?)
5.转到2,合并N-1次后结束
6.min即为所求,输出min
prim本身复杂度是O(n^2),合并n-1次,算法复杂度即为O(n^3),如果在prim中加堆优化,复杂度会降为O((n^2)logn)0.
#include <iostream> #include <cstdio> #include <sstream> #include <cstring> #include <map> #include <cctype> #include <set> #include <vector> #include <stack> #include <queue> #include <algorithm> #include <cmath> #include <bitset> #define rap(i, a, n) for(int i=a; i<=n; i++) #define rep(i, a, n) for(int i=a; i<n; i++) #define lap(i, a, n) for(int i=n; i>=a; i--) #define lep(i, a, n) for(int i=n; i>a; i--) #define rd(a) scanf("%d", &a) #define rlld(a) scanf("%lld", &a) #define rc(a) scanf("%c", &a) #define rs(a) scanf("%s", a) #define rb(a) scanf("%lf", &a) #define rf(a) scanf("%f", &a) #define pd(a) printf("%d ", a) #define plld(a) printf("%lld ", a) #define pc(a) printf("%c ", a) #define ps(a) printf("%s ", a) #define MOD 2018 #define LL long long #define ULL unsigned long long #define Pair pair<int, int> #define mem(a, b) memset(a, b, sizeof(a)) #define _ ios_base::sync_with_stdio(0),cin.tie(0) //freopen("1.txt", "r", stdin); using namespace std; const int maxn = 105, INF = 0x7fffffff; int n, m; int way[maxn][maxn], d[maxn], bin[maxn]; bool vis[maxn]; int contract(int &s, int &t) { mem(vis, false); mem(d, 0); int k, maxc, ans; rap(i, 1, n) { k = -1, maxc = -INF; rap(j, 1, n) if(!bin[j] && !vis[j] && d[j] > maxc) k = j, maxc = d[j]; if(k == -1) return ans; s = t, t = k, ans = maxc; vis[k] = true; rap(j, 1, n) if(!bin[j] && !vis[j]) d[j] += way[k][j]; } return ans; } int SW() { int mincut = INF, ans, s, t; rep(i, 1, n) { ans = contract(s, t); bin[t] = 1; mincut = min(ans, mincut); if(mincut == 0) return 0; rap(j, 1, n) if(!bin[j]) way[s][j] = (way[j][s] += way[j][t]); } return mincut; } int main() { while(scanf("%d%d", &n, &m) != EOF) { mem(way, 0); mem(bin, 0); int u, v, w; rap(i, 1, m) { rd(u), rd(v), rd(w); u++, v++; way[u][v] += w; way[v][u] += w; } cout << SW() << endl; } return 0; }