

/****************************************************/
/****************************************************/
/****************************************************/
下面是具体说明
1、FFT:频谱关于中间位置对称,只需要观察 0:1:N/2(这N/2+1个点)(时域采集N个点,频域只需要观察N/2+1个点)
2、MATLAB中FFT的频谱,应该看幅值
3、X轴频率点的设置:采样频率为Fs,频谱图显示的最高频率为Fs/2(采样定理)
:X轴频率点:(0:1:N/2)*Fs/N
4、复数幅值修正

5、

/****************************************************/
/****************************************************/
/****************************************************/
栗子及实践部分
一、信号

%% FFT clear;clc;close all Fs=1000; % 采集频率 T=1/Fs; % 采集时间间隔 N=2000; % 采集信号的长度--采样点数 f1=33; % 第一个余弦信号的频率 f2=200; % 第二个余弦信号的频率 t=(0:1:N-1)*T; % 定义整个采集时间点 t=t'; % 转置成列向量 y=1.2+2.7*cos(2*pi*f1*t+pi/4)+5*cos(2*pi*f2*t+pi/6); % 时域信号
二、绘制时域信号
%% 绘制时域信号
figure
plot(t,y)
xlabel('时间')
ylabel('信号值')
title('时域信号')
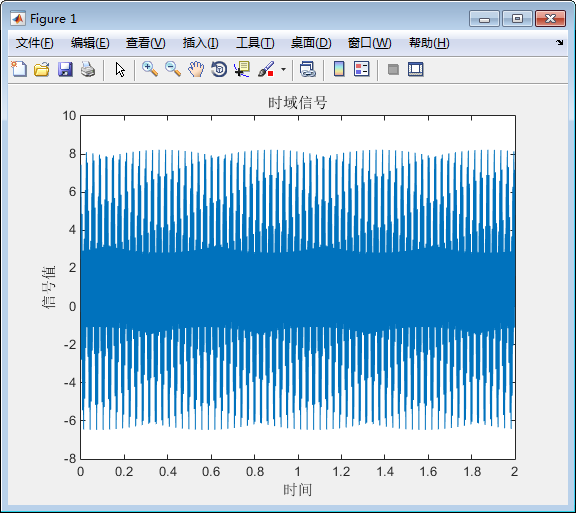
三、FFT变换、并绘制-幅值、实部、虚部
%% fft变换
Y=fft(y); % Y为fft变换的结果,为复数向量
A=abs(Y); % 复数的幅值(模)
RE=real(Y); % 复数的实部
IM=imag(Y); % 复数的虚部
%% 绘制fft变换结果(幅值,实部,虚部)
figure
subplot(3,1,1)
plot(0:1:N-1,A)
xlabel('序号 0 ~ N-1')
ylabel('幅值')
grid on
%% 频域只读取0:1:N/2
subplot(3,1,2)
plot(0:1:N-1,RE)
xlabel('序号 0 ~ N-1')
ylabel('实部')
grid on
subplot(3,1,3)
plot(0:1:N-1,IM)
xlabel('序号 0 ~ N-1')
ylabel('虚部')
grid on
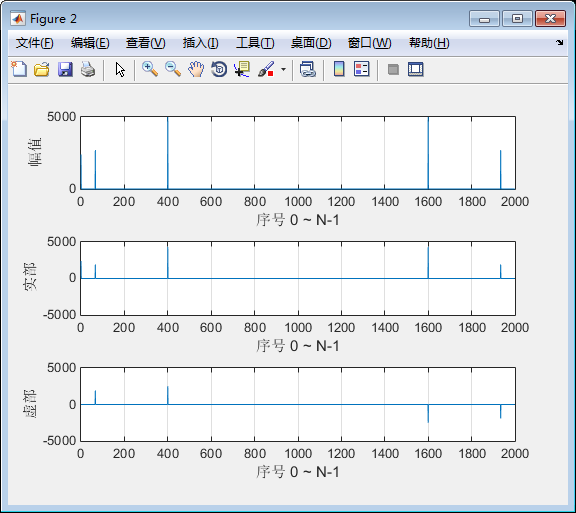
可以看出频域中的点关于(N/2)对称,所以只需要观察(0:1:N/2)
四、更改相位

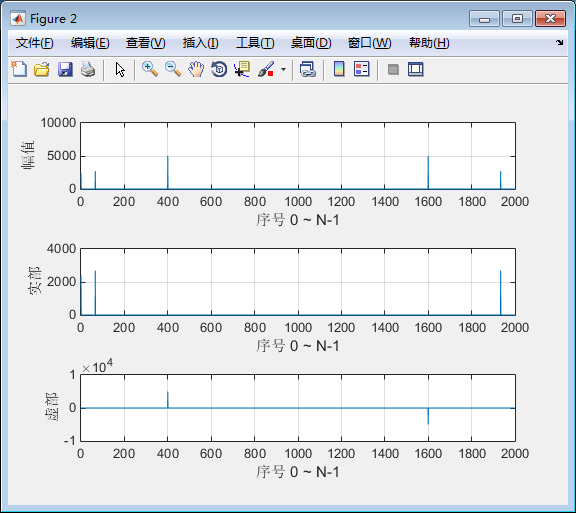
幅值不受影响,但实部或虚部的值,会出现0的情况==>看MATLAB中FFT的频谱,应该看幅值
绘制半谱图(幅值的)后--我们发现-幅值-相位-频率---均和时域对应不上。
==>进行幅值-修正
五、进行幅值-修正--并绘制图形
%% fft变换
Y=fft(y); % Y为fft变换结果,复数向量
Y=Y(1:N/2+1); % 只看变换结果的一半即可
A=abs(Y); % 复数的幅值(模)
f=(0:1:N/2)*Fs/N; % 生成频率范围
f=f'; % 转置成列向量
%% 幅值修正
A_adj=zeros(N/2+1,1);
A_adj(1)=A(1)/N; % 频率为0的位置
A_adj(end)=A(end)/N; % 频率为Fs/2的位置
A_adj(2:end-1)=2*A(2:end-1)/N;
%% 绘制频率幅值图
figure
subplot(2,1,1)
plot(f,A_adj)
xlabel('频率 (Hz)')
ylabel('幅值 (修正后)')
title('FFT变换幅值图')
grid on
%% 绘制频谱相位图
subplot(2,1,2)
phase_angle=angle(Y); % angle函数的返回结果为弧度
phase_angle=rad2deg(phase_angle);
plot(f,phase_angle)
xlabel('频率 (Hz)')
ylabel('相位角 (degree)')
title('FFT变换相位图')
grid on
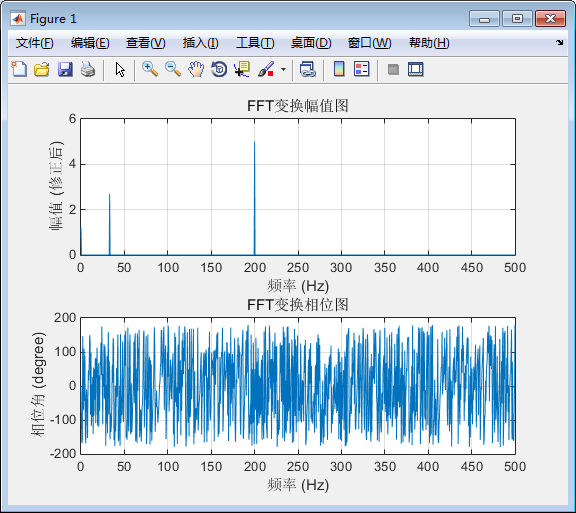
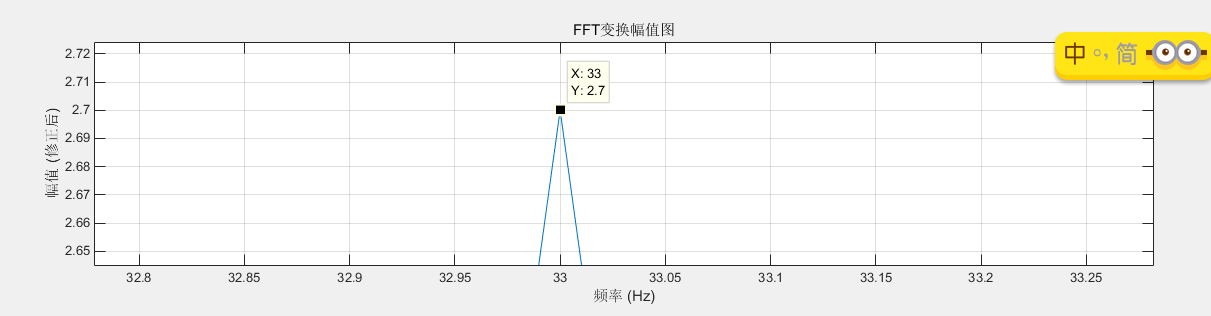
放大后可以看到,此时,幅值-频率都和时域一致
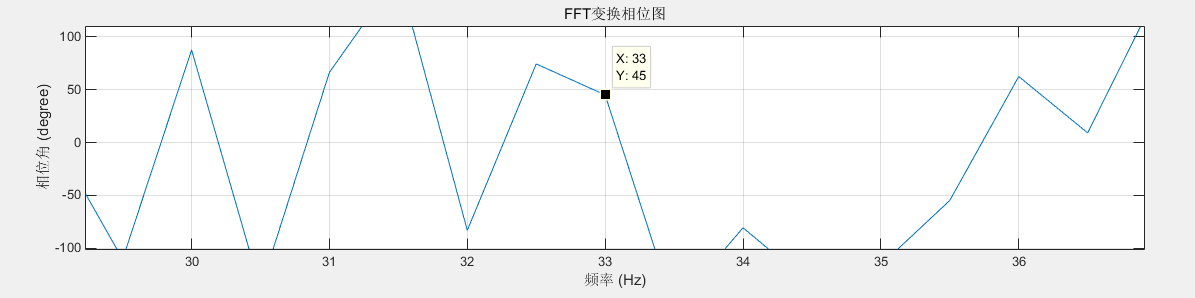
此时FFT的相位图是杂乱无章的--不用担心,没有频率处的相位是无意义的--我们只需要放大看各个(实际存在的)频率点的相位即可
可以看到--f1=33Hz处为45度,即pi/4--是正确的
六、实际操作:请分析一个未知的采集信号 (example.mat),并确定该采集信号的频率成分。其中, 信号的采集频率 Fs = 2500 Hz
代码
clear;clc;close all
load('example')
Fs=2500; % 采集频率
T=1/Fs; % 采集时间间隔
N=length(y); % 采集信号的长度
t=(0:1:N-1)*T; % 定义整个采集时间点
t=t'; % 转置成列向量
% 绘制时域信号
figure
plot(t,y)
xlabel('时间')
ylabel('信号值')
title('时域信号')
% fft变换
Y=fft(y); % Y为fft变换结果,复数向量
Y=Y(1:N/2+1); % 只看变换结果的一半即可
A=abs(Y); % 复数的幅值(模)
f=(0:1:N/2)*Fs/N; % 生成频率范围
f=f'; % 转置成列向量
% 幅值修正
A_adj=zeros(N/2+1,1);
A_adj(1)=A(1)/N; % 频率为0的位置
A_adj(end)=A(end)/N; % 频率为Fs/2的位置
A_adj(2:end-1)=2*A(2:end-1)/N;
% 绘制频率幅值图
figure
subplot(2,1,1)
plot(f,A_adj)
xlabel('频率 (Hz)')
ylabel('幅值 (修正后)')
title('FFT变换幅值图')
grid on
% 绘制频谱相位图
subplot(2,1,2)
phase_angle=angle(Y); % angle函数的返回结果为弧度
phase_angle=rad2deg(phase_angle);
plot(f,phase_angle)
xlabel('频率 (Hz)')
ylabel('相位角 (degree)')
title('FFT变换相位图')
grid on
