线段树是用于解决区间上问题的数据结构。用了分治的思想。
可以用线段树解决的问题通常都符合结合律。及满足一个询问包含的多个区间,可以用一个或几个更大的区间表示。(例如sum,min,max,xor...)
也就是说,父亲的值由他的孩子决定,通过孩子维护自己。而父亲的值是他的孩子集合的解。
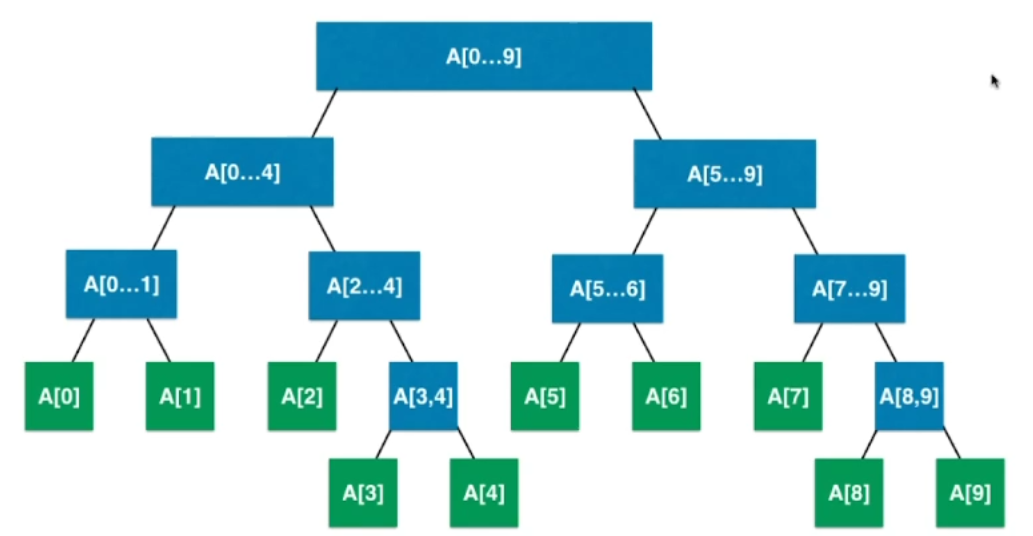
比方说,在上面的图片里。A[0...1]的值由A[0],A[1]共同维护,A[0...1]的值是包含A[0],A[1]的集合的解。
因此,通过对线段树的维护,我们可以很快地得到我们想要的区间内的信息。
我们将每一个区间(包括叶子结点)进行编号,从上到下从左到右。
我们可以发现线段树是一棵二叉树。
在上方的图片中,一共有10个叶子节点,但一共有19个节点。所以一般来说我们会开一个数组,长度在原始数据长度 L的4倍。
我们有,对任意非叶子节点 p,他的左儿子为 p*2,右儿子为 p*2+1。
在实际使用中,我们用位运算来获得一点加速。
1 // find sons 2 inline ll ls(ll p) {return p<<1;} // 计算左儿子的编号 3 inline ll rs(ll p) {return p<<1|1;} // 计算右儿子的编号
二进制左移一位代表 *2。左移后最后一位一定为0,所以 |1就相当于 +1。
我们在函数的最前面加 inline以减少不必要的信息入栈。尤其对于递归次数少,执行代码短的函数。
使用一个函数来维护 p的值。(在本文章里,我们已求区间和为例)
1 inline void up(ll p) // 用于维护 p的值 2 { 3 t[p]=t[ls(p)]+t[rs(p)]; 4 }
在拥有维护本层值的函数后,我们就可以建树了。
我们从第一层开始递归建树。
如果,当我现在包含的区间(l,r),l=r时,说明我已经分到了叶子节点。那我直接将本节点的值赋为我输入的数据。
否则,我不断将(l,r)分为(l,mid)和(mid+1,r)进行建树。
因为递归是先向下,后向上。所以我们在回溯时进行信息的维护。
1 // build the tree 2 inline void build(ll p,ll l,ll r) 3 { 4 if(l==r) {t[p]=a[l];return;} 5 ll mid=(l+r)>>1; 6 build(ls(p),l,mid); 7 build(rs(p),mid+1,r); 8 up(p); 9 }
接下来我们介绍有关线段树的修改。(本文章以加一个数为例)
每次修改一个区间或单点时,由于完全二叉树的深度为logN。所以复杂度为O(NlogN)。
但线段树的优点在于延迟更新。复杂度可以降至O(logN)。
我们用一个数组 tag记录 p的更新。
每次修改或查询时,只有用到 p下的区间时才会真正下传。
如果要修改区间完全包含此区间,那么直接更新此区间的值与 tag即可。
在修改完回溯时重新更新 p的值。
下传类似于维护本区间。
对于左右儿子,其 tag加上父亲的 tag,值为区间长(b-a+1)乘以父亲的 tag。
对于父亲,其 tag在下传后归零。
1 inline void down(ll p,ll l,ll r) 2 { 3 ll mid=(l+r)>>1; 4 tag[ls(p)]+=tag[p]; 5 t[ls(p)]+=(mid-l+1)*tag[p]; 6 tag[rs(p)]+=tag[p]; 7 t[rs(p)]+=(r-(mid+1)+1)*tag[p]; 8 tag[p]=0; 9 }
这是修改的代码。
1 // add the number 2 inline void add(ll p,ll l,ll r,ll nl,ll nr,ll k) 3 { 4 if(nl<=l&&r<=nr) 5 { 6 tag[p]+=k; 7 t[p]+=(r-l+1)*k; 8 } 9 down(p,l,r); 10 ll mid=(l+r)>>1; 11 if(nl<=mid) add(ls(p),l,mid,nl,nr,k); 12 if(mid+1<=nr) add(rs(p),mid+1,r,nl,nr,k); 13 up(p); 14 }
对于区间查询,使用同样的思路。
1 // query the number 2 inline ll query(ll p,ll l,ll r,ll nl,ll nr) 3 { 4 ll res=0; 5 if(nl<=l&&r<=nr) return t[p]; 6 down(p,l,r); 7 ll mid=(l+r)>>1; 8 if(nl<=mid) res+=query(ls(p),l,mid,nl,nr); 9 if(mid+1<=nr) res+=query(rs(p),mid+1,r,nl,nr); 10 return res; 11 }
参考博客:https://pks-loving.blog.luogu.org/senior-data-structure-qian-tan-xian-duan-shu-segment-tree