2020牛客寒假算法基础集训营1 honoka和格点三角形

https://ac.nowcoder.com/acm/contest/3002/A

题意

　　满足以下三个条件的三角形是“好三角形”。

　　　　1.三角形的三个顶点均为格点，即横坐标和纵坐标均为整数。
　　　　2.三角形的面积为 。
　　　　3.三角形至少有一条边和 轴或 轴平行。

　　在平面中选取一个大小为 的矩形格点阵，可以找到多少个不同的“好三角形”？

　　由于答案可能过大，请对 取模。

题解

　　计数。

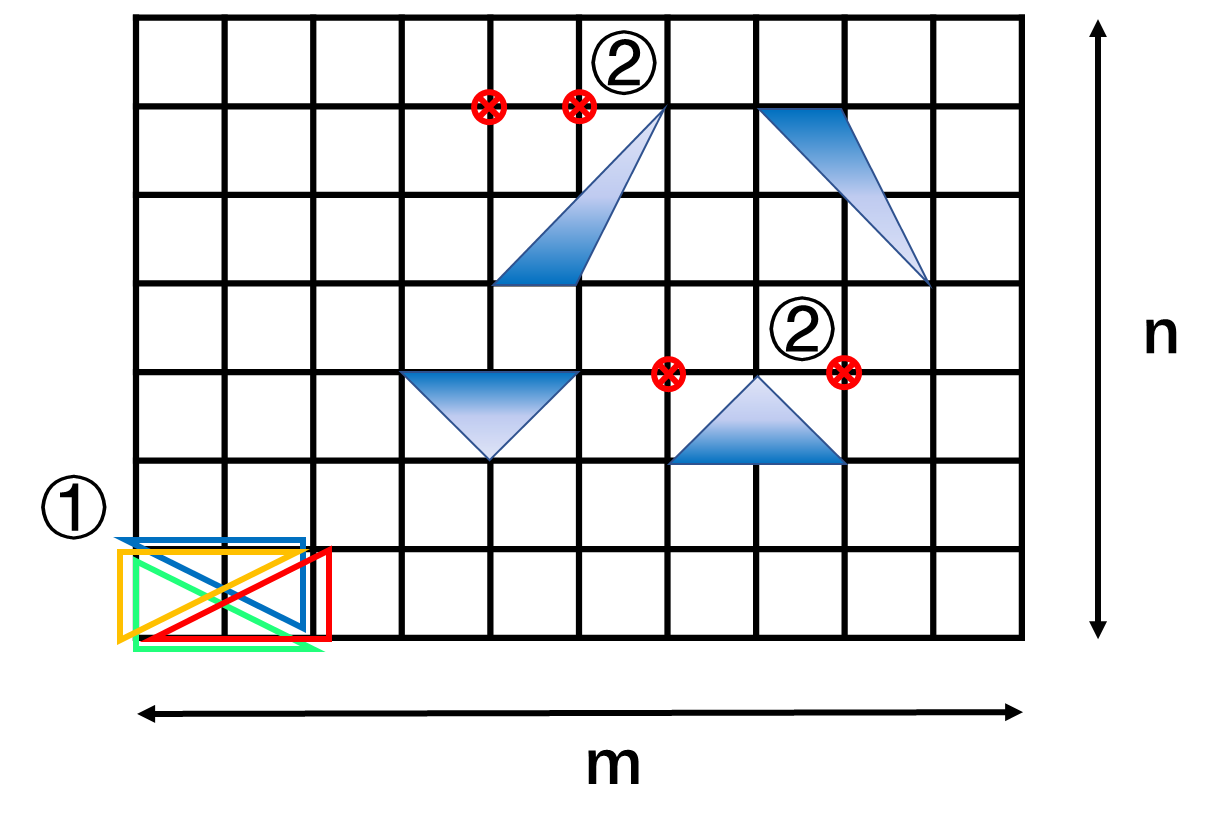
　　一. 三角形的两条边都与坐标轴平行

　　　  三角形为直角三角形。

　　　  大小为 1 * 2 矩形的在横轴上的情况为（n - 1），在竖轴上的情况为（m - 2），所以（n - 1）*（m - 2）。

　　　  大小为 2 * 1 矩形的在横轴上的情况为（n - 2），在竖轴上的情况为（m - 1），所以（n - 2）*（m - 1）。

　　　  又因为每种矩形可以分为四种三角形（ ① ），所以 4 *（（n - 1）*（m - 2） + （n - 2）*（m - 1））

　　二.三角形的一条边与坐标轴平行

　　　 三角形为等腰三角形。

　　　 与横轴平行（②）

　　    　　大小为 1 * 2 的三角形在横轴的情况为（n - 1），在竖轴的情况为（m - 2），顶点的情况为（n - 2），所以（n - 1）*（m - 2） * （n - 2）。

　　　　　又因为水平翻转，所以 2 *（n - 1）*（m - 2） * （n - 2）。

                 大小为 2 * 1 的三角形在横轴的情况为（n - 2），在竖轴的情况为（m - 1），顶点的情况为（n - 2），所以（n - 2）*（m - 1） * （n - 2）。

　　　　　又因为水平翻转，所以 2 *（n - 2）*（m - 1） * （n - 2）。

　　　 与竖轴平行

　　　　　 同理。

代码

#include <bits/stdc++.h>
using namespace std;
const long long mod=1e9+7;
int main()
{
    long long n,m,ans;
    scanf("%lld%lld",&n,&m);
    ans=4*((n-2)*(m-1)%mod+(n-1)*(m-2)%mod);
    ans=(ans+2*(n-2)%mod*(m-1)%mod*(n-2)%mod+2*(n-1)%mod*(m-2)%mod*(n-2)%mod)%mod;
    ans=(ans+2*(m-2)%mod*(n-1)%mod*(m-2)%mod+2*(m-1)%mod*(n-2)%mod*(m-2)%mod)%mod;
    printf("%lld",ans);
    system("pause");
    return 0;
}