定义
Dijkstra(迪杰斯特拉)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
原理
设图 G=(V,E) 所有顶点的集合为 V,起点为 S,最短路径树中包含的顶点集合为 S。在各计算步骤中,我们将选出最短路径树的边和顶点并将其添加至S。
对于各顶点 i,设仅经由S内的顶点的 s 到 i 的最短路径成本为 d[i], i 在最短路径树中的父节点为 p[i]。
①初始状态下将 S 置空。
初始化 s 的 d[s]=0;除 s 外,所有属于 V 的顶点 i 的 d[i]=∞。
②循环进行下述处理,直至 S=V 为止。
从 V-S 中选出 d[u] 最小的顶点 u。
将 u 添加至 S,同时将与 u 相邻且属于 V-S 的所有顶点 v 的值按照下述方式更新
if(d[u] + w(u,v) < d[v])
d[v] = d[u] + w(u,v) , p[v] = u ;
❗ 显然迪杰斯特拉算法并不能处理负权图。下图中A->B的最短路应为 3=8-5,但用此算法算出来的A->B的最短路为7。
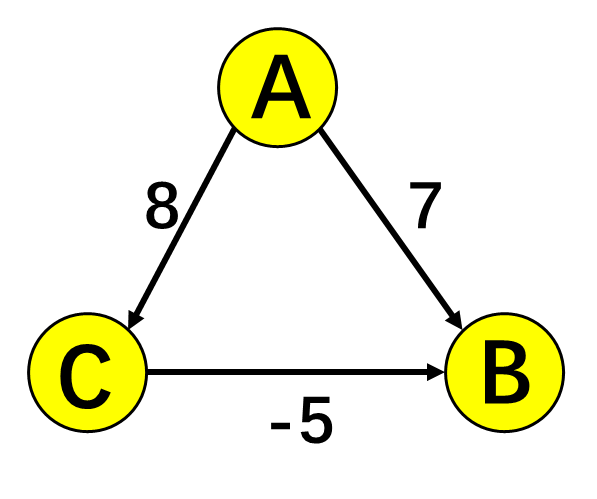
迪杰斯特拉最短路径算法和普利姆算法贼像。:)
实现

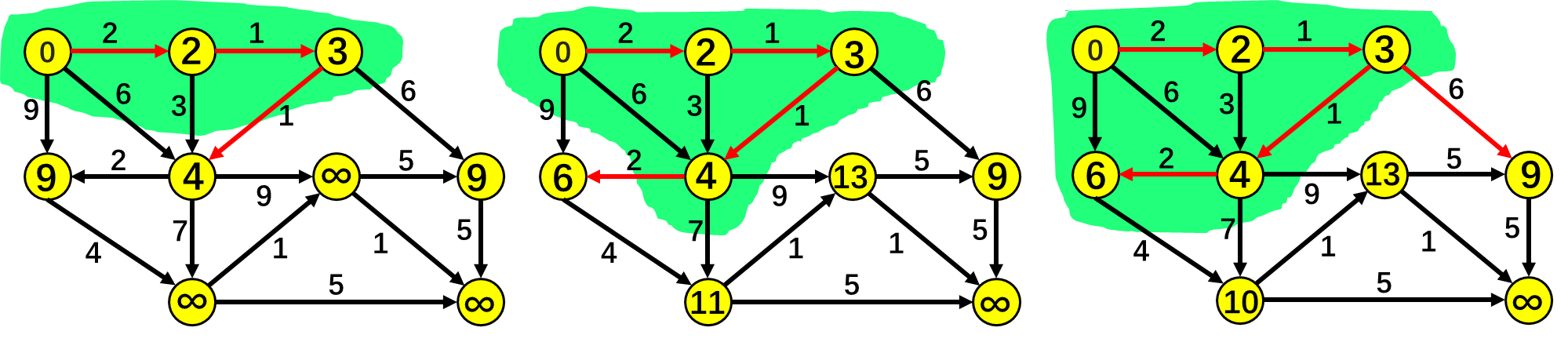
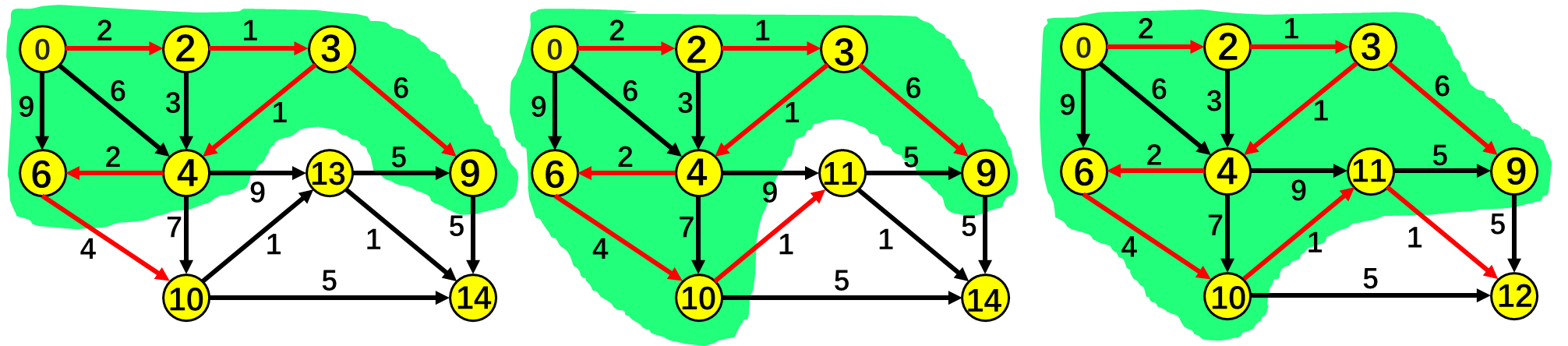
原算法
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
int v,w;
node(){}
node(int a,int b)
{v=a;w=b;}
};
vector<node> e[maxn];
int n,m;
void dij();
int main()
{
int i,u,v,w;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
e[u].push_back(node(v,w));
}
dij();
system("pause");
return 0;
}
void dij()
{
int dis[maxn],vis[maxn]={0},i,j,mmin,f;
fill(dis,dis+maxn,inf);
dis[1]=0;
for(i=1;i<=n;i++)
{
mmin=inf;
for(j=1;j<=n;j++)
if(!vis[j]&&dis[j]<mmin)
mmin=dis[f=j];
vis[f]=1;
for(j=0;j<e[f].size();j++)
{
if(dis[e[f][j].v]>dis[f]+e[f][j].w)
dis[e[f][j].v]=dis[f]+e[f][j].w;
}
}
for(j=1;j<=n;j++)
printf("1->%d %d
",j,dis[j]);
}
优先队列优化
#include<bits/stdc++.h>
using namespace std;
const int maxn=1005;
const int inf=0x3f3f3f3f;
struct node
{
int v,w;
node(){}
node(int a,int b)
{v=a;w=b;}
bool operator <(const node &n) const
{return w>n.w;}
};
vector<node> e[maxn];
int n,m;
void dij_queue();
int main()
{
int i,u,v,w;
scanf("%d%d",&n,&m);
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&w);
e[u].push_back(node(v,w));
}
dij_queue();
system("pause");
return 0;
}
void dij_queue()
{
int dis[maxn],vis[maxn]={0},u,v,w,i;
node p;
priority_queue<node> que;
que.push(node(1,0));
fill(dis,dis+maxn,inf);
dis[1]=0;
while(!que.empty())
{
p=que.top();que.pop();
u=p.v;
if(vis[u]) continue;
vis[u]=1;
for(i=0;i<e[u].size();i++)
{
w=e[u][i].w;v=e[u][i].v;
if(!vis[v]&&dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
que.push(node(v,dis[v]));
}
}
}
for(i=1;i<=n;i++)
printf("1->%d %d
",i,dis[i]);
}
挑战程序设计竞赛(第2版)