Kruskal算法 (克鲁斯卡尔)

定义

Kruskal算法是一种用来查找最小生成树的算法。

准备

树：如果一个无向连通图中不存在回路，则这种图称为树。

生成树 ：无向连通图G的一个子图如果是一颗包含G的所有顶点的树，则该子图称为G的生成树。

生成树是连通图的极小连通子图。这里所谓极小是指：若在树中任意增加一条边，则将出现一条回路；若去掉一条边，将会使之变成非连通图。

最小生成树：对无向连通图的生成树，各边的权值总和称为生成树的权，权最小的生成树称为最小生成树。

构成生成树的准则有三条：

① 必须只使用该网络中的边来构造最小生成树。

② 必须使用且仅使用n-1条边来连接网络中的n个顶点

③ 不能使用产生回路的边。

原理

  ①  将图 G=(V,E) 的边  按权值升序排列。

  ②  设最小生成树的边的集合为 K,并将其初始化为空。

  ③  在保证  不出现环的前提下，按 i = 1, 2, ..., |E| 的顺序将  添加至 K，直至|K| = |V| - 1  

    （一般利用并查集判断是否形成回路）

实现

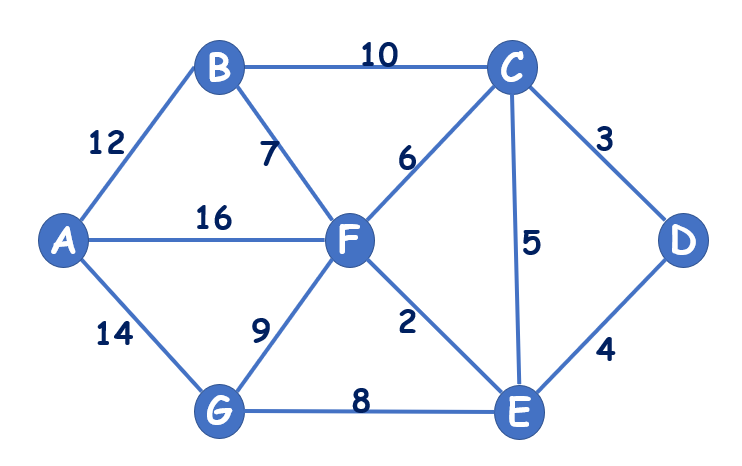
   ① 排序 

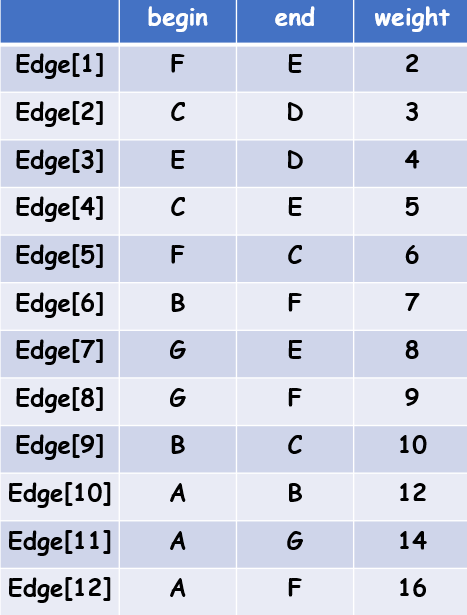
   ②从小到大判断每条边。

  

代码

#include<bits/stdc++.h>
using namespace std;
struct node
{
 int u,v,w;
 node(){}
 node(int a,int b,int c) {u=a;v=b;w=c;}
 bool operator <(const node &n) const
 {return w<n.w;}
};
int f[1000];
vector<node> edge;
int find(int p)
{return f[p]==-1?p:f[p]=find(f[p]);}
int main()
{
  fill(f,f+1000,-1);
  int u,v,w,i,x,y,sum=0,cnt=0,n;
  scanf("%d",&n);
  for(i=0;i<n;i++)
  {
    scanf("%d%d%d",&u,&v,&w);
    edge.push_back(node(u,v,w));
  }
  sort(edge.begin(),edge.end());
  for(i=0;i<edge.size();i++)
  {
      x=find(edge[i].u);
      y=find(edge[i].v);
      if(x!=y)
      {
         f[y]=x;
         sum+=edge[i].w;
         printf("%d %d %d
",edge[i].u,edge[i].v,edge[i].w);
         if(++cnt==n-1) break;
      }
    }
  printf("最小生成树权值为%d",sum);
  system("pause");
  return 0;
}