2017-2018-1 20155303 《信息安全系统设计基础》第三周学习总结
本周学习任务:《深入理解计算机系统》第2章 信息的表示和处理(教材导读)
————————CONTENTS————————
教材学习中的问题和解决过程
『问题一』:
课本P22提到:
使用32位表示数据类型int,计算表达式200*300*400*500会得出结果-884901888
这个结果是如何得到的呢?
『问题一解决』:
在计算器上分别模拟64位和32位计算机计算200*300*400*500的值:

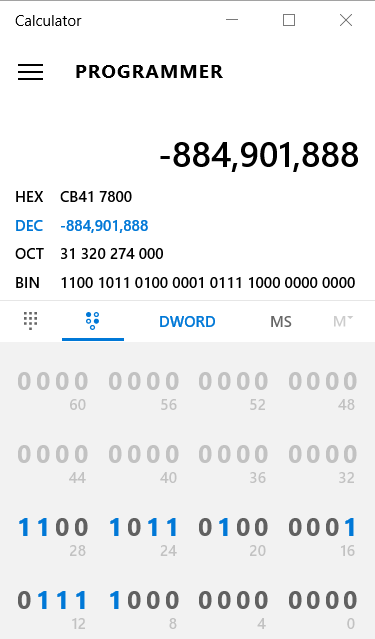
对比可以发现,在32位的机器上发生了溢出,只保留末32位,所以得到了-884901888这个值。
『问题二』:
课本P31程序中len为size_t类型,观察程序的功能发现len仅仅用在for循环的终止条件判断中,为什么不直接用int类型呢?
『问题二解决』:
查阅资料了解到,size_t类型是一个基本的无符号整数的C / C + +类型, 它是sizeof操作符返回的结果类型, 该类型的大小可选择。因此,它可以存储在理论上是可能的任何类型的数组的最大大小。 换句话说,一个指针可以被安全地放进为size_t类型(一个例外是类的函数指针,但是这是一个特殊的情况下)。 size_t类型通常用于循环、数组索引、大小的存储和地址运算。(百度百科)
由此得知,在标准C库中定义的(或32位系统)为unsigned int,在64位系统中为 long unsigned int。不同平台的size_t会用不同的类型实现,因此,使用size_t而非int或unsigned能够提升代码的可扩展性。

在/usr/include/asm-generic路径下的posix_types.h文件中,我们可以查询到相关说明:
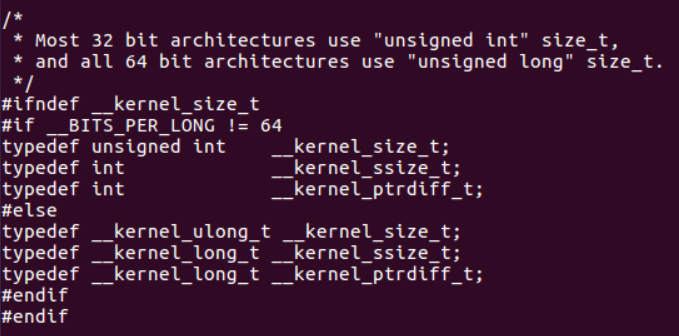
『问题三』:
课本P33提到:
对数值12345编码,整型为0x00003039,而浮点数为0x4640E400
将十六进制模式扩展成二进制形式,可以发现一个有13个相匹配的位的序列。是如何得到的呢?
『问题三解决』:
12345的整数表示为:
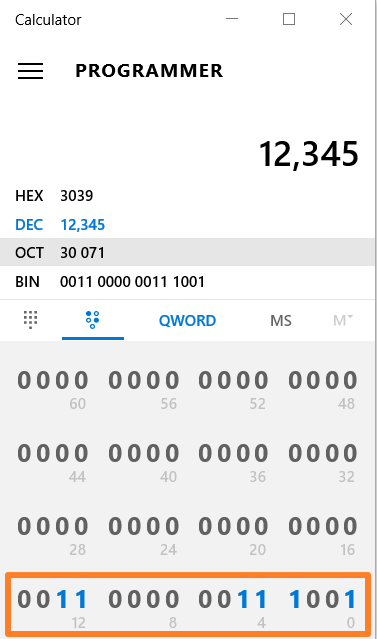
在IEEE 754 Calculator查看其浮点数格式为:
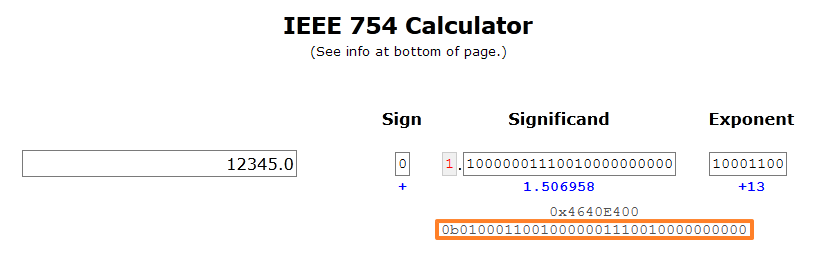
这是因为,这两种格式使用不同的编码方法。针对整型数字,是按照我们熟知的方法;而对于浮点数的处理方法有所不同。可以看到,对于浮点数的编码由三个部分组成:符号(sign)、尾数(significand)与阶码(exponent)。
12345的二进制表示为[11000000111001],将二进制小数点左移13位,得到规格化表示:12345=$1.1000000111001_2 x 2^13$。构造小数字段,需要去掉开头的1,并在末尾添上10个0,得到二进制表示[10000001110010000000000]。构造阶码字段,用13加上偏置量127,得到140,二进制为[10001100]。再加上符号位的0,即得到二进制浮点数表示为01000110010000001110010000000000。
『问题四』:
课本P65关于问题“编写函数,判断参数x和y相加是否产生溢出”给出了一个错误的示范(练习题2.31),这种方法错误之处在哪?
『问题四解决』:
练习题2.31给出的程序如下:
int tadd_ok(int x, int y)
{
int sum = x+y;
return (sum-x == y)&&(sum-y == x);
}
补码加法会形成一个阿贝尔群,所以不管是否有溢出,都满足sum-xy且sum-yx。
正确的方法为:
int uadd_ok(unsigned x, unsigned y) //确定无符号加法是否溢出
{
unsigned sum = x+y;
return sum >= x;
}
int tadd_ok(int x, int y) //确定补码加法是否溢出
{
int sum = x+y;
int neg_over = x < 0 && y < 0 && sum >=0; //判断负数溢出
int pos_over = x >= 0 && y >= 0 && sum < 0; //判断正数溢出
return !neg_over && !pos_over
}
『问题五』:
课本P87练习题2.54的G项如何理解?
『问题五解决』:
回顾IEEE表示浮点数的方法,符号位(sign)位于二进制表示法的首位。乘法和除法结果的符号是由两个参与运算的数字决定的。因此,即使d*d的结果可能溢出至+∞,但不影响其符号位。
代码调试中的问题和解决过程
『问题一』:
运行时提示段错误(核心已转储)的解决方法(以P38练习题2.11为例)。
『问题一解决』:
编写的程序如下,使用a^a=0这一属性完成数值交换:
#include <stdio.h>
#include <stdlib.h>
void inplace_swap(int *x, int *y);
void reverse_array(int a[], int cnt);
int main(){
int a[3] = {1, 2, 3};
int b[4] = {1, 2, 3, 4};
reverse_array(a, 3);
reverse_array(b, 4);
for(int i = 0; i <= 2; i++){
printf("%d ",a[i]);
}
printf("
");
for(int j = 0; j <= 3; j++){
printf("%d ",b[j]);
}
printf("
");
return 0;
}
void inplace_swap(int *a, int *b)
{
*b = *a ^ *b;
*a = *a ^ *b;
*b = *a ^ *b;
}
void reverse_array(int a[], int cnt){
int first, last;
for(first = 0, last = cnt-1; first < last; first++,last++)
{
inplace_swap(&a[first], &a[last]);
}
}
编译运行时,却出现了这样的问题:

查阅资料了解到,出现段错误(核心已转储)的原因有以下几种可能:
- 访问不存在的内存地址
- 访问系统保护的内存地址
- 访问只读的内存地址
- 空指针废弃
- 堆栈溢出
- 内存越界(数组越界,变量类型不一致等)
- ...
本程序出现错误属于哪种情况呢?可以使用gcc和gdb调试程序。
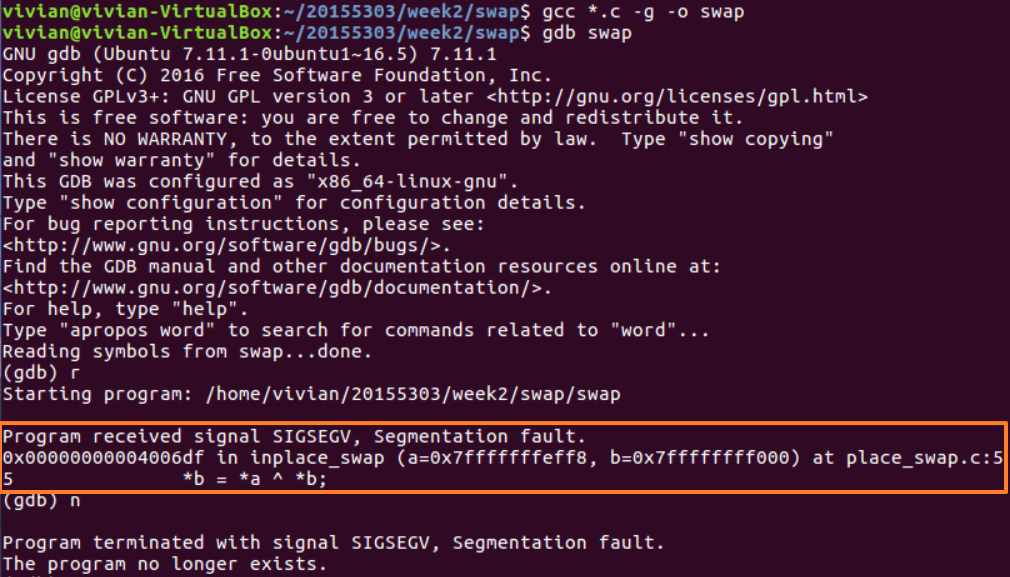
从结果看出,程序收到 SIGSEGV 信号,触发段错误,并提示地址0x00000000004006df,在取指针内容进行运算时出现错误。
可以通过man 7 signal查看SIGSEGV的信息:
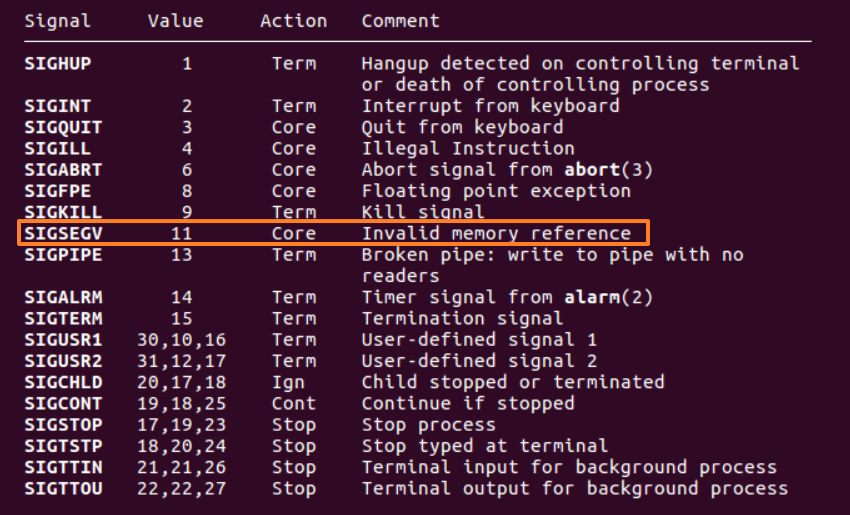
由此排查,发现函数reverse_array()中循环的操作应为first++,last--。first++,last++会造成数组越界,出现段错误提示。
通过man 7 signal,可以看到SIGSEGV默认的处理程序(handler)会打印段错误信息,并产生 core 文件,由此我们可以借助于程序异常退出生成的 core 文件中的调试信息,使用 gdb 工具来调试程序中的段错误。
默认情况下是不产生 core 文件的,首先可以查看一下系统 core 文件的大小限制:

通过ulimit -c 1024命令,设置core文件的大小位1024kb。运行程序,发生段错误生成 core 文件;加载 core 文件,使用 gdb 工具进行调试:
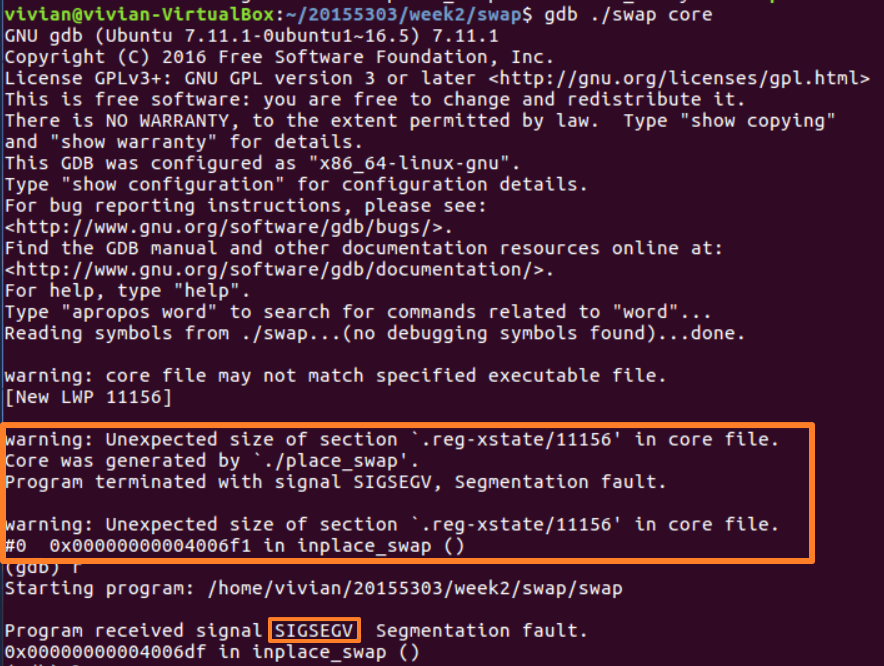
同样可以显示出错误信息。
核心转储文件(Core File)也是一种ELF文件,可以通过readelf -h core查看core文件的相关信息:
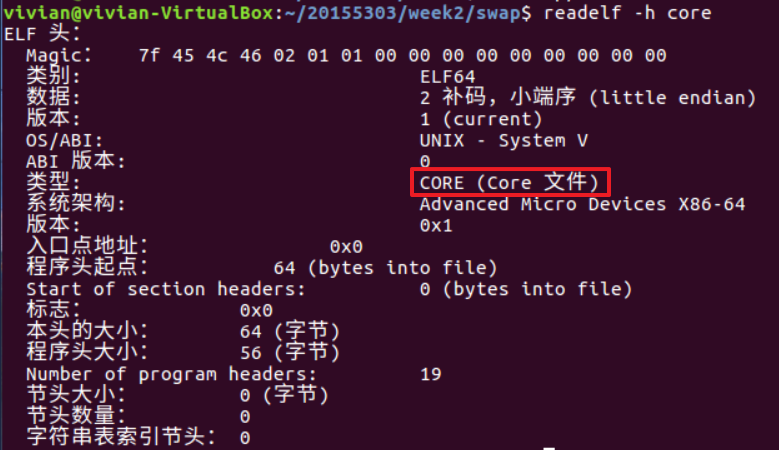
『问题二』:
通过对课本P54代码进行测试,验证补码数进行符号扩展的方式。
『问题二解决』:

可以看出,尽管-12345的补码表示和53191的无符号表示在16位字长时是相同的,但在32位字长时,-12345的十六进制表示为0xFFFFCFC7,而53191的十六进制表示为0x0000CFC7。这是使用最高位进行符号扩展造成的不同。
『问题三』:
课本P58练习题2.25为什么会出现段错误?如何改正?
程序如下:
float sum_elements(float a[], unsigned length){
int i;
float result = 0;
for(i = 0; i <= length-1; i++){
result += a[i];
}
return result;
}
『问题三解决』:
当length为0时,由于length是无符号的,所以将使用无符号运算。0-1结果为UMax。对于任何数而言,都是小于UMax的,所以,将访问数组a的非法元素,造成段错误。
- 修改方案1:将length定义为int类型;
- 修改方案2:将for循环的测试条件改为i<length。
『问题四』:
课本P86总结了int、float和double格式之间进行强制类型转换时,程序改变数值和位模式的原则。试写代码测试一下。
『问题四解决』:
1.int→float:数字不会溢出,但可能被舍入。
在程序中使用断言:
#include <stdio.h>
#include <assert.h>
float i2f(int a); //int转float
float i2f(int a){
return (float)a;
}
int main(){
assert(i2f(16777217)==16777217.0);//测试舍入
return 0;
}
运行时却出现了错误:

为什么会出现这种情况呢?
int型的有效位数是31,而float型小数域的有效位只有23位,也就是说如果int a的二进制的有效位超过了24位,那么float型的小数域的精度就不够了。于是进行了舍入。
以16777217为例,16777217=2^24 +1,因此需舍入为2^24,代码改为assert(i2f(16777217)==16777216.0);就可以了。
2.int/float→double:double有更大的范围(也就是可表示值的范围),也有更高的精度(也就是有效位数),因此能够保留精确数值。
3.double→float:范围缩小,可能溢出成+∞或-∞;也有可能被舍入。
这里举一个溢出的例子:
assert(d2f(123.456789e100)==123.456789e100);运行结果为:

可以看出,由于float表示范围和精度的限制,转换过程造成了溢出。
4.float/double→int:向零舍入,或为整数不确定值。
以下断言均成立:
assert(f2i(5.00)==5);//测试正常情况
assert(f2i(1.99)==1);//测试向零舍入
assert(f2i(-1.99)==-1);//测试向零舍入
但如果不能为该浮点数找到一个合理的整数近似值,就会产生整数不确定(integer indefinite)值。比如:+1e10。

可以看出,每一次的运行结果都是不同的。
代码托管
代码量截图:
结对及互评
-
队友:20155213
-
他的博客中值得学习的或问题:
-
他的代码中值得学习的或问题:
-
结对照片:
-
结对学习内容:
上一周在编写myod相关程序时,遇到了一些无法解决(目前也正在研究)的问题,比如Linux下curse.h库的使用等等。为了更好地实现功能,队友在我的思路的基础上,又提出了很多宝贵的改进意见,帮助我解决问题,并写了一篇博客进行总结。题目虽小,但我们在不断迭代修改的过程中,受益匪浅。
学习感悟和思考
本周主要学习了课本第二章“信息的表示和处理”,深入研究了计算机算术运算的特性等等,了解了可以表示的值的范围和不同算术运算的属性,从而保证编写的程序能在全部的数值范围内正确工作,而且具有可以跨越不同机器、操作系统和编译器组合的可移植性。算术运算的数学属性决定了稍不留神就会产生溢出等错误,算术溢出是造成程序错误和安全漏洞的一个常见根源,因此在编写程序时要格外注意。
在学习课本内容的过程中遇到了大量的公式,其推导过程让人眼花缭乱。但耐心看完之后发现只不过是把直觉的认知转化成了经过严格证明的推理,其实并不难理解;再佐以适当的练习,把实践过程中遇到的问题都弄明白,也就大致理解计算机算术运算的原则了。
比如本章末关于IEEE浮点表示的讲解,在学习本章之前我有过大致的了解,一次是上学期编写Java程序遇到的浮点数精度误差问题,还有一次是暑假复习C语言格式化输出函数printf。两次都只是一知半解,查了资料还是满头雾水,这次自然在心里抵制,觉得浮点数的表示方法晦涩难懂。所以在学习时格外小心,一个字一个字读,遇到不明白的就在IEEE 754 Calculator上模拟计算机的操作,或者动手验证。一章学下来,也算对IEEE浮点数表示法有了最基本的感性和理性认识,下次再遇到浮点数的精度误差问题,就能进行基本的分析,而不是百思不得其解,眉毛胡子一把抓了。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 20篇 | 400小时 | |
| 第一周 | 50/50 | 1/1 | 8/8 | 了解计算机系统、静态链接与动态链接 |
| 第三周 | 451/501 | 2/3 | 27/35 | 深入学习计算机算术运算的特性 |