作为与FCOS和FSAF同期的Anchor-free论文,FoveaBox在整体结构上也是基于DenseBox加FPN的策略,主要差别在于FoveaBox只使用目标中心区域进行预测且回归预测的是归一化后的偏移值,还有根据目标尺寸选择FPN的多层进行训练,大家可以学习下
来源:晓飞的算法工程笔记 公众号
论文: FoveaBox: Beyound Anchor-Based Object Detection

Introduction
论文认为anchor的使用不一定是最优的搜索目标的方式,且受人眼视网膜中央凹(fovea)的启发:视觉区域的中部有最高的视觉敏锐度,所以提出了anchor-free目标检测方法FoveaBox。
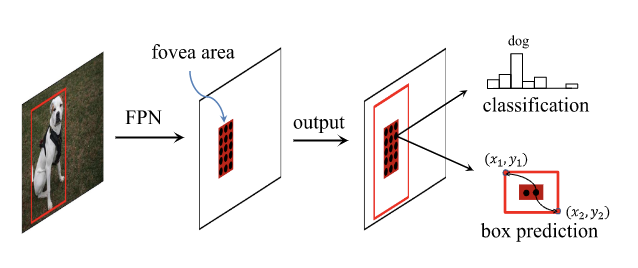
FoveaBox联合预测每个有效位置为目标中心的可能性及其对应目标的尺寸,输出类别置信度以及用以转化目标区域的尺寸信息。如果大家看过很多Anchor-free的检测方案,可能觉得论文的实现方案很常见,的确,其实这篇文章也是Anchor-free井喷初期的作品,整体思路很纯粹,也是很多大佬都想到的思路,在阅读时需要关注以下细节:
- 以目标的中心区域进行分类预测与回归预测
- 将回归预测的是归一化后的偏移值
- 训练时可指定FPN多层同时训练
- 提出特征对齐模块,使用回归的输出来调整分类的输入特征
FoveaBox

Object Occurrence Possibility
给定GT目标框\((x_1, y_1, x_2, y_2)\),将其映射到特征金字塔层\(P_l\):
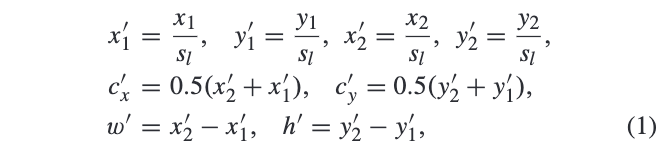
\(s_l\)为特征层相对于输入的stride,正样本区域\(R^{pos}\)为大致为映射框的缩小版本:
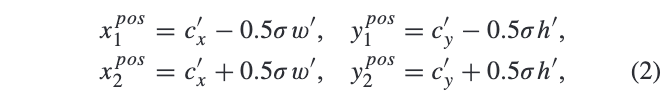
\(\sigma\)为人为设定缩放因子。在训练阶段,正样本区域内的特征点标记为对应的目标类别,其余的区域为负样本区域,特征金字塔每层的输出为\(C\times H\times W\),\(C\)为类别总数。
Scale Assignment
网络的目标是预测目标的边界,直接预测是不稳定的,因为目标尺寸的跨度很大。为此,论文将目标尺寸归为多个区间,对应特征金字塔各层,各层负责特定尺寸范围的预测。给予特征金字塔\(P_3\)到\(P_7\)基础尺寸\(r_l=2^{l+2}\),则层\(l\)负责的目标尺寸范围为:
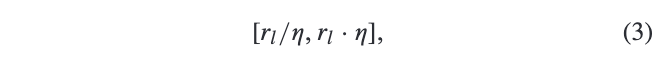
\(\eta\)为人工设置的参数,用于控制特征金字塔每层的回归尺寸范围,不在该层尺寸范围内的训练目标则忽略。目标可能落到多个层的尺寸范围内,这时使用多层进行训练,多层训练有以下好处:
- 邻接的特征金字塔层通常有类似的语义信息,可同时进行优化。
- 大幅增加每层的训练样本数,使得训练过程更稳定。
Box Prediction
在预测目标尺寸时,FoveaBox直接计算正样本区域\((x,y)\)到目标边界的归一化的偏移值:
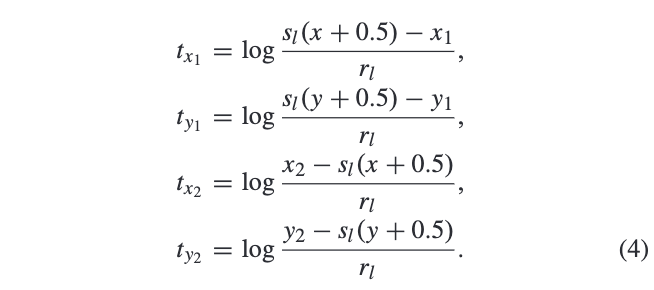
公式4先将特征金字塔层的像素映射回输入图片,再进行偏移值的计算,训练采用L1损失函数。
Network Architecture
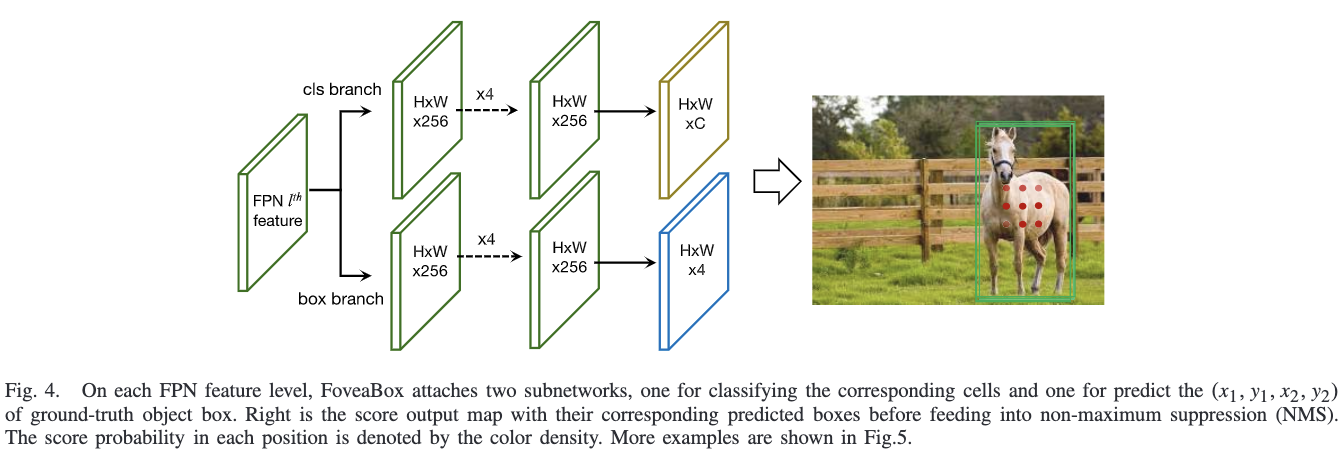
网络结构如图4所示,主干网络采用特征金字塔的形式,每层接一个预测Head,包含分类分支和回归分支。论文采用较简单的Head结构,使用更复杂的Head可以获得更好的性能。
Feature Alignment
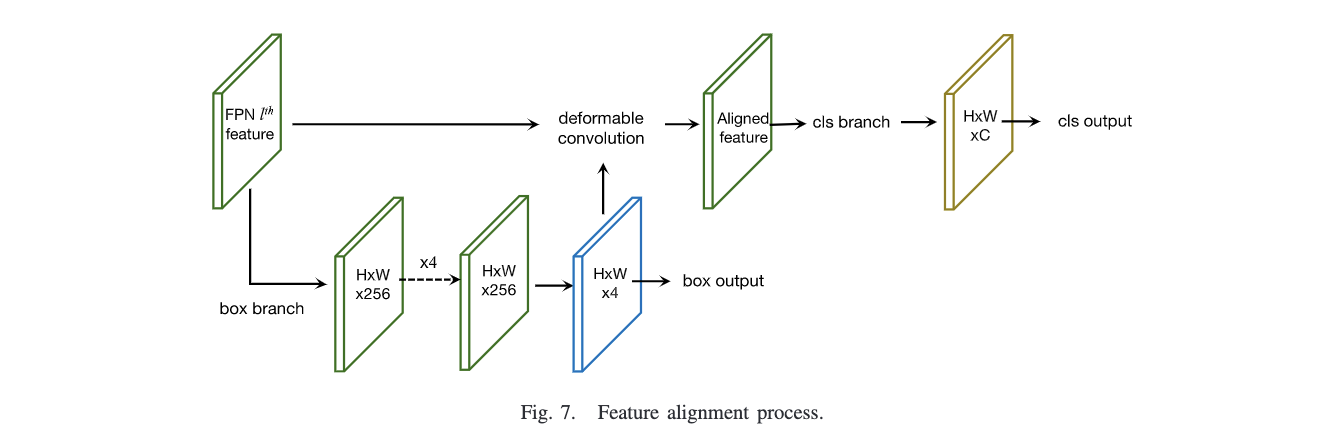
论文提出了特征对齐的trick,主要是对预测Head进行改造,结构如图7所示,
Experiment
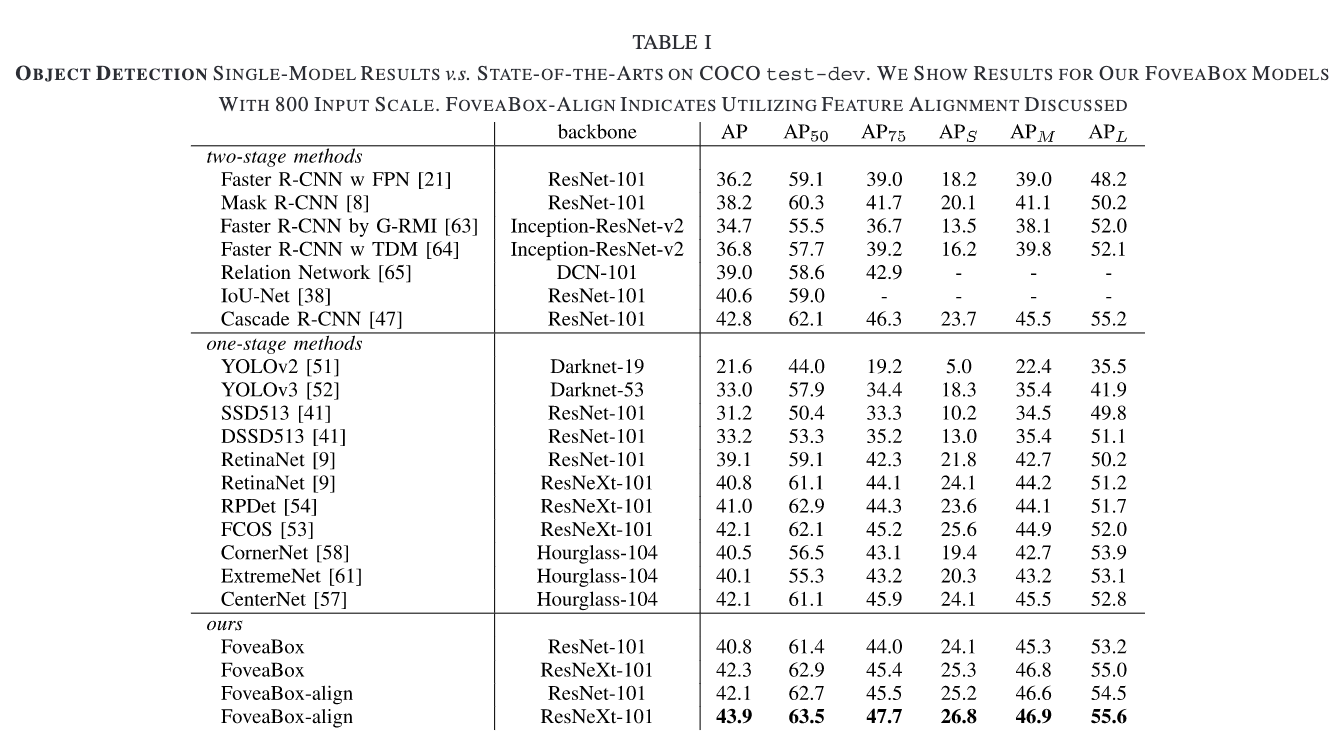
与SOTA方法进行对比。
Conclusion
作为与FCOS和FSAF同期的Anchor-free论文,FoveaBox在整体结构上也是基于DenseBox加FPN的策略,主要差别在于FoveaBox只使用目标中心区域进行预测且回归预测的是归一化后的偏移值,还有根据目标尺寸选择FPN的多层进行训练。由于FoveaBox的整体实现方案太纯粹了,与其它Anchor-free方法很像,所以一直投稿到现在才中了,作者也是相当不容易。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
