Non-local操作是早期self-attention在视觉任务上的尝试,核心在于依照相似度加权其它特征对当前特征进行增强,实现方式十分简洁,为后续的很多相关研究提供了参考
来源:晓飞的算法工程笔记 公众号
论文: Non-local Neural Networks

Introduction

卷积操作通常在局部区域进行特征提取,想要获取范围更广的特征信息需要重复进行卷积操作来获得,这样不仅耗时还增加了训练难度。为此,论文提出高效的non-local操作,将特征图上的特征点表示为所有特征点的加权和,用于捕捉覆盖范围更广的特征信息。non-local操作也可以用于含时序的任务中,如图1的视频分类任务,可综合几帧的特征来增强当前帧的特征。
non-local操作主要有以下优点:
- 相对于叠加卷积的操作,non-local可通过特征点间的交互直接捕捉更广的特征信息。
- 从实验结果来看,简单地嵌入几层non-local操作就能高效地提升网络性能。
- non-local操作支持可变输入,可很好地与其它网络算子配合。
Non-local Neural Networks
Formulation
首先定义通用的non-local操作:

\(i\)为特征图上将要计算特征值的位置坐标,\(j\)为特征图上的所有位置坐标,\(x\)为对应位置上的输入特征,\(y\)为增强后的输出,\(f\)计算\(i\)和\(j\)之间的相似性,\(g\)则用于对\(j\)的特征进行转化,\(\mathcal{C}\)用于对输出进行归一化。
简而言之,non-local的核心就是计算当前位置的特征与特征图所有特征间的相似性,然后根据相似性对所有特征加权输出。相对于卷积和全连接等参数固定的操作,non-local更加灵活。
Instantiations
在实现时,函数\(f\)和函数\(g\)的选择很多。为了简便,函数\(g\)选择为线性变换\(g(x_j)=W_gx_j\),\(W_g\)为可学习的权重矩阵,一般为\(1\times 1\)的卷积。而函数\(f\)则可以有以下选择(论文通过实验发现函数\(f\)的具体实现影响不大):
-
Gaussian

\(x^T_i x_j\)为点积相似度,也可采用欧氏距离,\(\mathcal{C}(x)={\sum}_{\forall j}f(x_i, x_j)\),归一化类似于softmax操作。
-
Embedded Gaussian
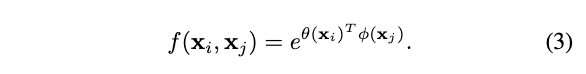
\(\theta(x_i)=W_{\theta}x_i\)和\(\phi(x_j)=W_{\phi}x_j\)为两个线性变换,\(\mathcal{C}(x)={\sum}_{\forall j}f(x_i, x_j)\),这个实现与self-attention十分接近。
-
Dot product

先线性变换,然后通过点积计算相似度,\(\mathcal{C}(x)=N\),有助于简化梯度计算。
-
Concatenation

直接将特征conate起来,通过权重向量\(w^T_f\)转化为标量输出,\(\mathcal{C}(x)=N\)。
Non-local Block
将公式1的non-local操作修改成non-local block,可插入到当前的网络架构中,non-local block的定义为:

公式6将non-local操作的输出线性变换后与原特征进行相加,类似于residual block的嵌入方式。
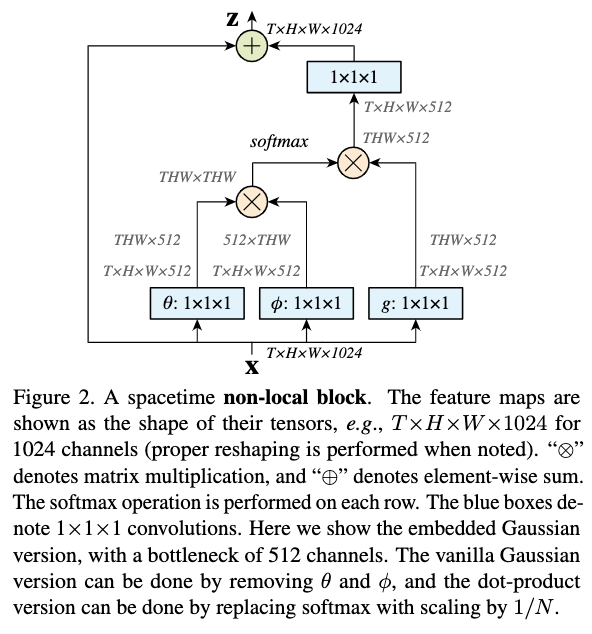
non-local block的一种实现方式如图2所示,首先对\(x\)进行3种不同的线性变换,然后按照公式1得到输出特征,再与原特征进行相加,基本上跟self-attention是一样的。
Experiment

各种对比实验,表2a为函数\(f\)的实现对比,可以看到影响不是很大。

视频分类对比。

COCO上的分割、检测、关键点对比。
Conclusion
Non-local操作是早期self-attention在视觉任务上的尝试,核心在于依照相似度加权其它特征对当前特征进行增强,实现方式十分简洁,为后续的很多相关研究提供了参考。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
