#587Div3
A
题意
- 给定一个字符串只含 (a,b)
- 使得每个前缀的 (a) 和 (b) 的个数相同(当然是偶数位上的
解法
- 一路改,哪个多就变成另一种
100分代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
char x,good[200005];
int n,one,two,ans;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++){
cin>>x;
if(x=='a') one++;
else two++;
if(i%2) {
good[i]=x;
continue;
}
if(one==two){
good[i]=x;
continue;
}
ans++;
if(one>two) good[i]='b',two++,one--;
else good[i]='a',one++,two--;
}
printf("%d
",ans);
// cout<<c<<endl;
for(int i=1;i<=n;i++) cout<<good[i];
return 0;
}
B
题意
- 排序
解法
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
int n,ans;
struct node{
int id,x;
}d[1005];
bool cmp(node a,node b){
return a.x >b.x ;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&d[i].x),d[i].id =i;
sort(d+1,d+n+1,cmp);
for(int i=1;i<=n;i++)
ans+=d[i].x*(i-1)+1;
printf("%d
",ans);
for(int i=1;i<=n;i++) printf("%d ",d[i].id );
return 0;
}
D
题意
- 有 (n) 个数,有 (y) 个数是被减掉了若干个(z)后的,最初都是 (x)
- 求最小的 (y) 和 (z)
解法
- 从小到大排序,我们按照最大数当 (x) ,求出其他数和最大值的差,求这些差值的最大公约数。就是最少的人数。差值的和是剪掉多少个 (z)
代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#define ll long long
using namespace std;
int n;
ll ans,gd;
ll a[200005];
ll gcd(ll a,ll b){
if(b==0) return a;
return gcd(b,a%b);
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%lld",&a[i]);
sort(a+1,a+n+1);
for(int i=1;i<n;i++){
a[i]=a[n]-a[i];
ans+=a[i];
gd=gcd(gd,a[i]);
}
printf("%lld %lld",ans/gd,gd);
return 0;
}
E1
题意
类似这样的数列 1 2 3 4 5 6 7 8 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6......
求第 (n) 项
(n<10^9)
解法
按个数分组,第一组是1 第二组是 1 2 第三组是 1 2 3 第n组是 1 2 3 4 5 ...n
暴力找到在哪个组
再预处理出1-n个数的第几项是0-9中的哪个数
暴力在这个组内,找到答案
100分代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int Q,res,cnt,maxx;
int num[500005],p[500005],now[500005];
struct node{
int id,k,ans;
}q[505];
bool cmp(node a,node b){
return a.k <b.k ;
}
bool cmp2(node a,node b){
return a.id <b.id ;
}
int main()
{
scanf("%d",&Q);
for(int i=1;i<=Q;i++){
scanf("%d",&q[i].k);
q[i].id =i;
maxx=max(maxx,q[i].k);
}
sort(q+1,q+Q+1,cmp);
maxx=sqrt(2*maxx)+1;
for(int i=1;i<=maxx;i++){
int x=i,cnt=0;
while(x){
now[++cnt]=x%10;
x/=10;
}
num[i]=num[i-1]+cnt;
while(cnt){
++res;
p[res]=now[cnt];
--cnt;
}
}
int from=1,last=0;
for(int i=1;i<=Q;i++){
while(from<=maxx){
if(num[from]+last<q[i].k){
last+=num[from++];
continue;
}
q[i].k -=last;
q[i].ans =p[q[i].k];
break;
}
}
sort(q+1,q+Q+1,cmp2);
for(int i=1;i<=Q;i++) printf("%d ",q[i].ans );
return 0;
}
E2
n<10^18
- 首先二分在哪个组,然后二分在这个组的哪个位置
- 考虑
- 1
- 1 2
- 1 2 3
- 1 2 3 4
- 1 2 3 4 5
- 1 2 3 4 5 ....9
- 1 2 3 4 5 6 ... 10
- 设位数是 (n)
- 上面这个三角形前x行的位数和,可以通过把位数分类,位数相同的在一类。
- 这样就可以如下图一样求
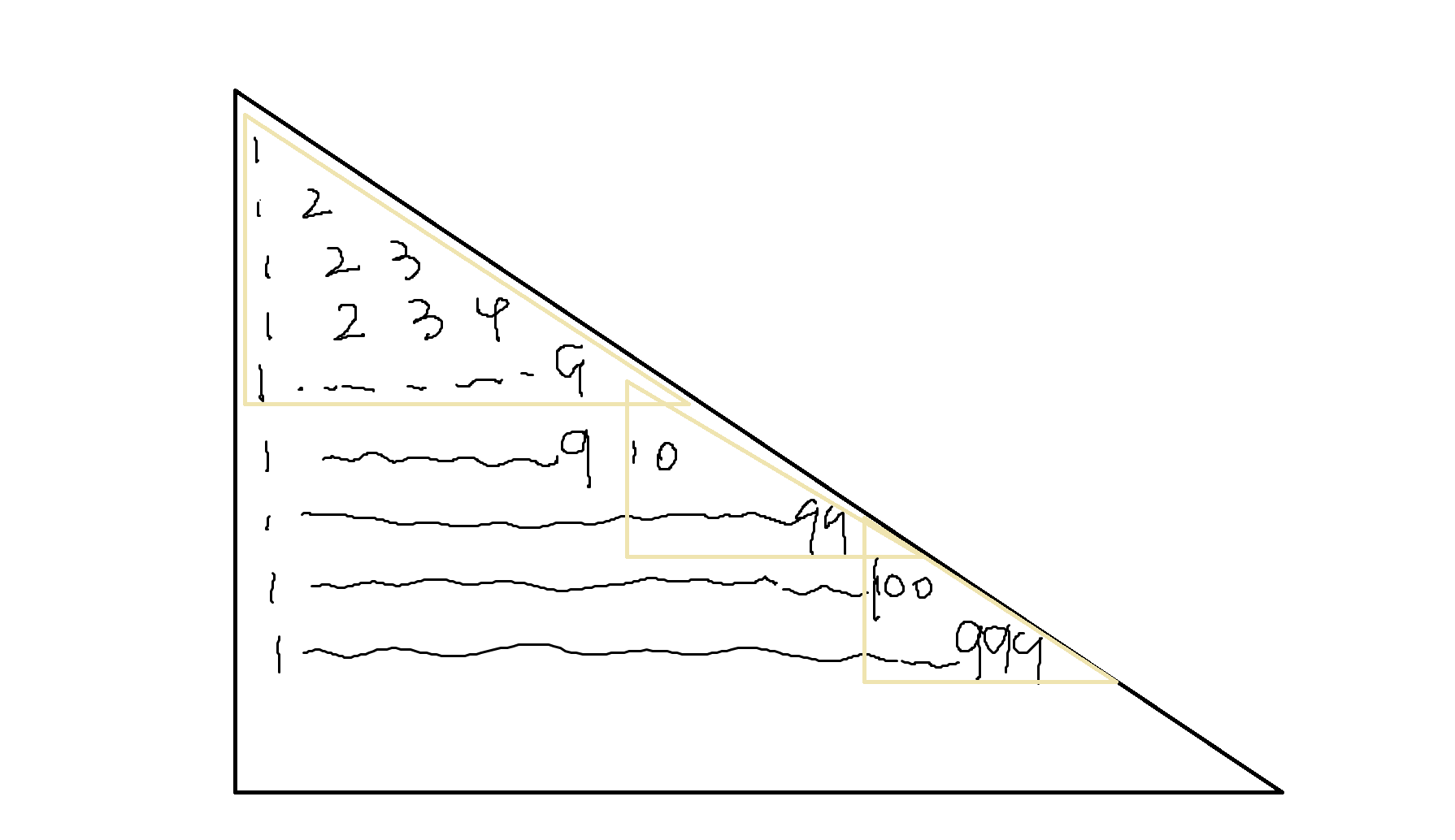
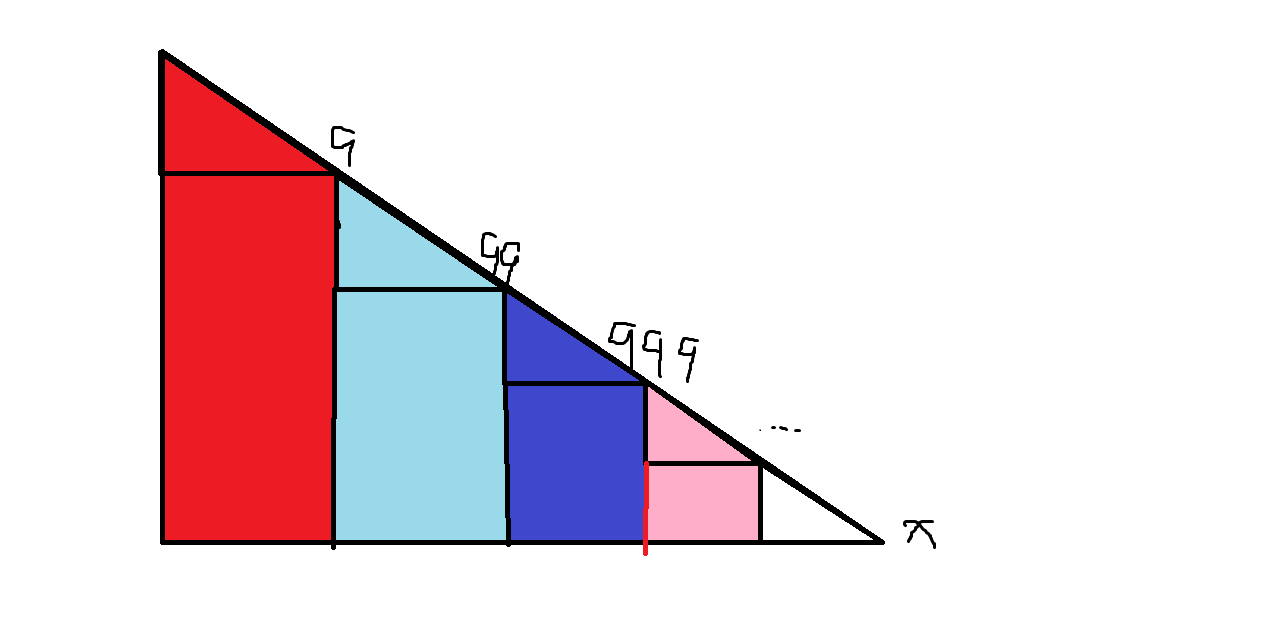
每一个三角形的数位和是 (j*(9*i)*(9*i+1)/2) ,每个三角形下的矩形面积是 (j*9*i*(x-10*i+1))
(j) 是指这一类数的位数, (i=10^{j-1})
三角形算和相当于是一个等差数列求和
-
注意边界,因为10是算在第二组的
-
然后二分出组后,再二分在组中的位置
-
看下面找规律
1 2 3 4 5 6 7 8 9
(1*9*10^0=1*(9-1+1))
10 11 12 13 14 15 16 .... 99
(2*9*10^1=2*(99-10+1))
100 101 102 103 104 105 106 107 .....999
(3*9*10^3=3*(999-100+1))
(10^x) (10^x+1) (10^x+2) (10^x+3) (...10^{x+1}-1)
((x+1)*9*10^{x+1}=(x+1)*(10^{x+1}-1-10^x+1))
- 令 (i=10^{x},j=x+1)
- 每种数位相同的数有 (9*i*10*j) 个,遇到不是10的整数倍的,就 ((n-i+1)*j) 个
100分代码
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
ll n,x;
int T;
ll check1(ll x){
ll now=0;
for(ll i=1,j=1;i<=x;i*=10,j++){
if(10*i<=x) now+=(9*i*(x-i*10+1)*j)+j*(9*i*(1+9*i))/2;
else now+=j*(x-i+1)*(x-i+2)/2;
if(now>1e18) return 1e18;
}
return now;
}
ll check2(ll x){
ll now=0;
for(ll i=1,j=1;i<=x;i*=10,j++){
if(i*10<=x) now+=9*i*j;
else now+=(x-i+1)*j;
if(now>1e18) return 1e18;
}
return now;
}
int main()
{
scanf("%d",&T);
while(T--){
scanf("%lld",&x);
ll l=0,r=1e9,mid;
while(l<=r){//二分组数
mid=(l+r)>>1;
if(check1(mid)<x) l=mid+1;
else r=mid-1;
}
x-=check1(r);
r=l;
l=1;
while(l<=r){//二分组中的第几个数
mid=(l+r)>>1;
if(check2(mid)<x) l=mid+1;
else r=mid-1;
}
x-=check2(r);
ll res=l,cnt=0;
while(res){
++cnt;
res/=10;
}
x=cnt-x;
for(ll i=1;i<=x;i++) l/=10;
printf("%lld
",l%10);
}
return 0;
}