2021牛客多校第三场 C.Minimum grid (思维 + 二分图)

一般来说棋盘问题都会与二分图或者生成树有关。

一开始我也是往二分图上去想的，

首先考虑行最大值和列最大值的最大值，记为 x，找到最大值需要等于 x 的行和列，设有 n 行和 m 列的最大值需要等于 x。原本是需要在每一行、每一列共 n + m 个位置放置 x，发现如果在他们交叉位置放置 x的话，可以少放置一些 x，每有一对行和列匹配，就可以少放置一个 x，如此一来转换成了二分图最大匹配问题

但是我看了看数据范围

n <= 2e3, m <= 8e5, k <= 1e6

假设行列拆点，那么点数为 2e3，之后边数为8e5, 那么相乘为1.6e9这不是妥妥爆吗。之后就写了一个贪心，直接无了。

（贪心其实就是如果这个位置行列值相同的话，这个地方肯定要取，之后其他地方就无所谓了。但是这样的话有可能会导致下面的情况

     1     1

1   x     x

1   x     x

你会把四个位置都取上，导致最后的答案偏多。

之后看网上的题解，发现竟然还是二分图。之所以可以用二分图做的原因是因为题目中有一句话：保证一个数字在行列值中不会出现超过500次。

不如我们想想二分图匹配到底在干什么吧，二分图匹配其实是枚举每个左部点，之后去找增广路的一个过程，所以复杂度其实是O (左部点数 * 找增广路所需要经过的边)

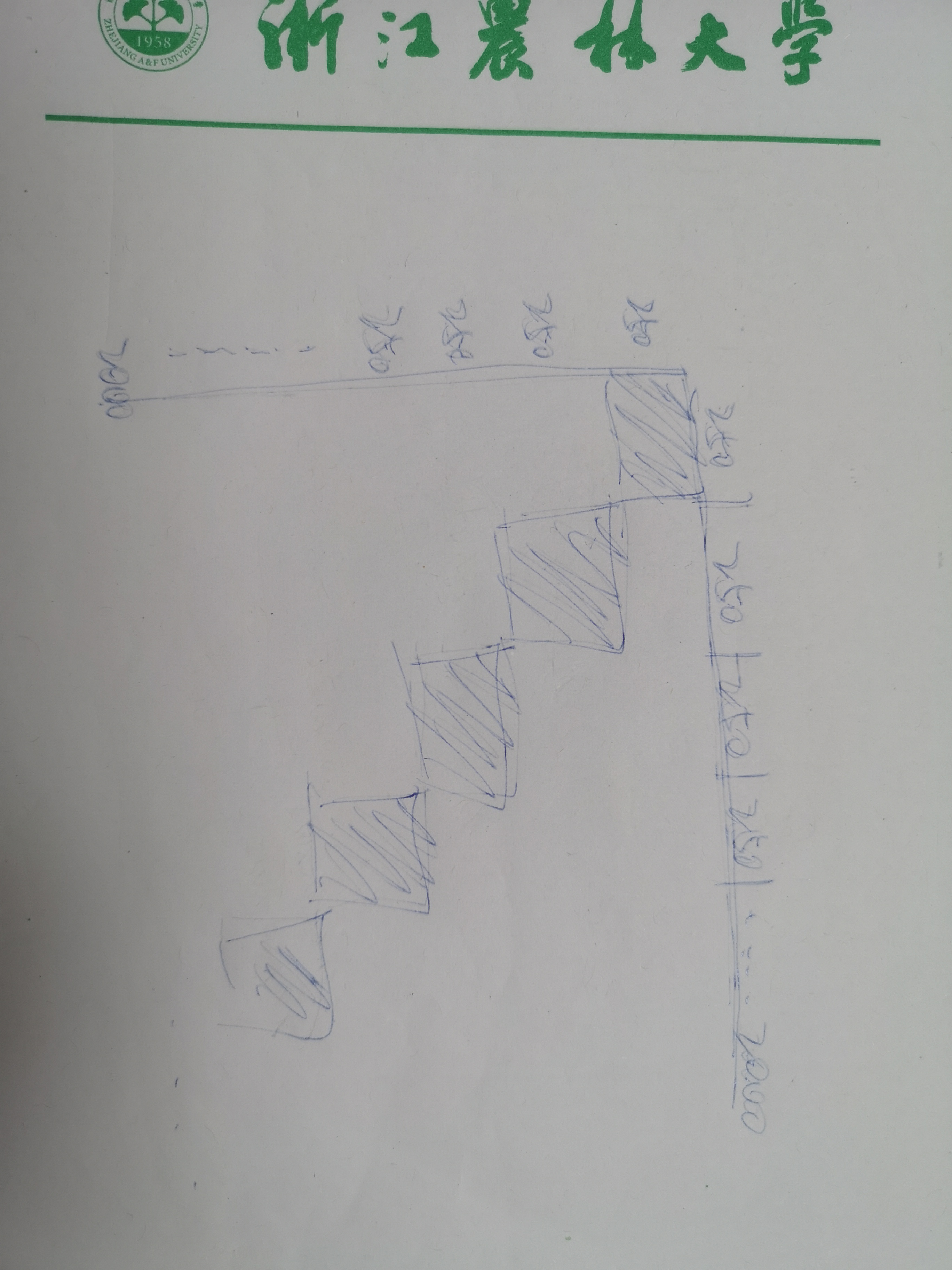
现在我们来重新计算一下复杂度，假设相同数字拉满，那么在每一个块里，最多会有250 * 250 = 6e4的边数。（相同数字不超过500，那么就让行列都出现250次，所以相同的块内边数就为250*250

那么复杂度O(NM) = 2e3 * 6e4 = 1e8就可以跑过了！淦！

就只需要在行列值相同的地方建边就好了，之后跑一个二分图匹配，如果这个行被match了代表就有一个位置同时取到了行列最大值，那么这个行的贡献就可以消去。

以下是ac代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<int, int> pii;
const int inf = 0x3f3f3f3f; ///1061109567
const int maxn = 2e3 + 10;

int n, m, k;
int row[maxn], col[maxn];

vector<int> E[maxn];
int nx, ny; ///左部、右部点数
int mx[maxn], my[maxn], vis[maxn];
int sta[maxn], top;

bool DFS(int u) {
    for (auto v : E[u]) {
        if (!vis[v]) {
            sta[++top] = v;
            vis[v] = 1;
            if (my[v] == 0 || DFS(my[v])) {
                my[v] = u, mx[u] = v;
                return 1;
            }
        }
    }
    return 0;
}

int main() {
    scanf("%d%d%d", &n, &m, &k);
    nx = ny = n;
    for (int i = 1; i <= n; ++ i) scanf("%d", &row[i]);
    for (int i = 1; i <= n; ++ i) scanf("%d", &col[i]);
    for (int i = 1; i <= m; ++ i) {
        int x, y; scanf("%d%d", &x, &y);
        if (row[x] == col[y]) E[x].push_back(y);
    }
    for (int i = 1; i <= n; ++ i) {
        if (mx[i] == 0) {
            while (top) vis[sta[top--]] = 0;
            if (DFS(i)) ;
        }
    }
    ll ans = 0;
    for (int i = 1; i <= n; ++ i) {
        ans += row[i] + col[i];
        if (mx[i]) ans -= row[i];
    }
    printf("%lld
", ans);
    return 0;
}