尺取法也叫双指针。
应用尺取法很重要的一个地方就是满足区间单调性。
什么叫区间单调性呢？
比如假设都是正数的数组，你选定了一段[L, R]，当R变大时，这一段的区间和会不断增大，而当L增大时，区间和会不断减小，这就是区间单调性了。
还有就是出现 >= k个不同字符的区间，当R变大时，区间中的字符个数会变大或者不变，而当L增大时，区间中的字符个数会减小或者不变。
这两个例子是不是能感受到一点尺取法的应用条件了呢。
大部分时间尺取法都会跟算贡献结合在一起（所以算贡献真的很重要啊喂）
试过来，好像是这种写法尺取的写法会快点，我想了一下可能是因为if 比 while 快吧。或者是因为if使得这个程序更快的跳出了
按理来说不会那么卡复杂度，所以还是挑选自己更好理解的方式来写。
（BTW，前++与前--会比后++与后--快哦~，也就几十ms（逃
while (1) { if (右边界不满足条件 && 不超过上界) { 右界变动，计算右界改变对此时状态的影响， } if (退出条件) break; else if (满足条件) { 计算贡献，左界变动，计算左界变动对此状态的影响 } }
现在就放几道题目来感受一下吧。
给出一个数n。你要求一段连续的数，这些数的平方和等于n。
/*poj headers*/ #include <map> #include <set> #include <queue> #include <vector> #include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 1e5+10; int main() { ll n; while (~scanf("%lld", &n)) { ll L = 0, R = 0, sum = 0; vector<pair<ll, ll> > p; while (1) { if (sum < n) { ++ R; sum += R*R; } if (R * R > n) break; else if (sum >= n) { if (sum == n) p.push_back({L+1, R}); ++ L; sum -= L * L; } } printf("%d ", p.size()); for(ll i = 0;i < p.size();i++) { printf("%lld",p[i].second-p[i].first+1); for(ll j = p[i].first;j <= p[i].second;j++) { printf(" %lld", j); } puts(""); } } return 0; }
现在给你一个整数 n，你要告诉他这个数字有多少种不同的连续素数和表示方式。
#include <map> #include <set> #include <queue> #include <vector> #include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 1e5+10; int tot, n; int prime[maxn]; void init() { prime[++tot] = 2, prime[++tot] = 3; for (int i = 4; i <= 10000; ++ i) { int flag = 0; for (int j = 2; j*j <= i && !flag; ++ j) if (i % j == 0) flag = 1; if (!flag) prime[++tot] = i; } } int main() { init(); while (~scanf("%d", &n), n) { int L = 0, R = 0, sum = 0; int cnt = 0; while (1) { if (sum < n) { ++ R; sum += prime[R]; } if (R > tot) break; else if (sum >= n) { if (sum == n) ++ cnt; ++ L; sum -= prime[L]; } } printf("%d ", cnt); } return 0; }
给你一串字符，问你至少出现k个不同数字的区间。
这里用到了算贡献，问你至少为k，我们知道当[L, R]的区间满足==k这个条件时，
那么[L, R+1] , [L, R+2], [L, R+3] ....[L, n]的区间肯定都是满足条件的。所以就是n - R + 1。
#include <bits/stdc++.h> using namespace std; typedef long long ll; int main() { int T; scanf("%d", &T); while (T--) { char str[1000000+10]; scanf("%s", str+1); int n = strlen(str+1); unordered_map<char, int> mp; int k; scanf("%d", &k); int L = 1, R = 0, cnt = 0; ll ans = 0; while (1) { if (cnt < k) { ++ R; ++ mp[str[R]]; if(mp[str[R]] == 1) ++ cnt; } if (R > n) break; else if(cnt==k) { ans = ans+n-R+1; -- mp[str[L]]; if(mp[str[L]]==0) -- cnt; ++ L; } } printf("%lld ", ans); } return 0; }
给你一个数组，问你有多少对a,b满足|x[b] - x[a]| <= k (a < b)
这题二分也可以做，lower_bound码量会小一点，但是时间会大比双指针多个log（也没小多少。
我们发现绝对值这个条件，其实是为了取消(a < b)这个条件的。
因为如果 |x[b] - x[a] | <= k，但是a > b 的话，其实把a,b交换就好了。所以我们可以把题目要求变得严格一点。
sort一遍变成， x[b] - x[a] <= k, a < b，这样就会非常好做了。剩下的就是双指针的的事了。
（sort一遍取消绝对值其实是非常常见的操作，当然如果没遇到过应该也能想到吧）
#include <map> #include <set> #include <queue> #include <vector> #include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 1e5+10; ll val[maxn]; int main() { int T; scanf("%d", &T); while (T--) { ll n, k; scanf("%lld%lld", &n, &k); for (int i = 1; i <= n; ++ i) { scanf("%lld", &val[i]); } sort(val+1, val+1+n); ll L = 1, R = 2, ans = 0; while (1) { if (R <= n && val[R]-val[L] <= k) ++ R; if (L == n+1) break; if (R == n+1 || val[R]-val[L] > k) { ans += (R-L-1); ++ L; } } printf("%lld ", ans); } return 0; }
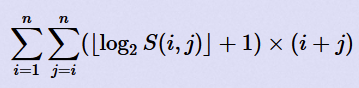
题意非常的简单，就是求（所有（区间和取log）+1）*（区间端点和））的和。但是却很难想。
首先我们发现ai >= 0 所以前缀和是满足区间加法的。
观察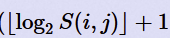
发现其实这个式子就是位数。之后观察范围发现位数最大也就35位（10^10）
那么就找到了突破点了。枚举位数，之后用双指针确定范围即可。
这里具体讲讲双指针怎么做好了。因为求得是一段区间，之后区间的端点其实是不固定的。那么我们其实就可以枚举左端点，
之后通过双指针找使得sum[L] - sum[i-1] (前缀和相减就是区间和，所以这里是[i, L] )>= 当前枚举位数,R也是同理。
之后计算贡献即可。
这道题不是很好写成上面的双指针格式所以就没写。
#include <map> #include <set> #include <queue> #include <vector> #include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> using namespace std; typedef long long ll; const int maxn = 1e5+10; ll val[maxn], dic[36], sum[maxn]; int main() { int T; scanf("%d", &T); dic[0] = 0, dic[1] = 2; for (int i = 2; i <= 35; ++ i) dic[i] = (dic[i-1] << 1); while (T--) { int n; scanf("%d", &n); for (int i = 1; i <= n; ++ i) { scanf("%lld", &val[i]); sum[i] = sum[i-1] + val[i]; } ll ans = 0; for (int bit = 1; bit <= 35; ++ bit) { ll L = 1, R = 1; for (int i = 1; i <= n; ++ i) { L = max(1ll*i, L); while (L <= n && sum[L] - sum[i-1] < dic[bit-1]) ++ L; while (R <= n && sum[R] - sum[i-1] < dic[bit]) ++ R; if (L < R) ans += bit*(1ll*i*(R-L) + (R-L)*(R+L-1)/2); } } printf("%lld ", ans); } return 0; }
找一个面积最小的矩阵，使得矩阵里的" . "的数量 >= k
二维前缀和预处理， 之后枚举矩阵的上界行与下界行，再通过双指针来寻找最小答案。
这里写成上面if格式会更慢。我想了一下，可能是因为返回前缀和常数比较大。
#include <map> #include <set> #include <queue> #include <vector> #include <cstdio> #include <cstring> #include <cstdlib> #include <iostream> #include <algorithm> using namespace std; const int N = 3e2+10; int sum[N][N]; int r, c, k; int _range(int x1, int y1, int x2, int y2) { return sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]; } int main() { while (~scanf("%d%d%d", &r, &c, &k)) { if (r == 0 && c == 0 && k == 0) break; char str[N]; for (int i = 1; i <= r; ++ i) { scanf("%s", str+1); for (int j = 1; j <= c; ++ j) { sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + (str[j]=='.'); } } int ans = r*c; for (int i = 1; i <= r; ++ i) { for (int j = i; j <= r; ++ j) { int L = 1, R = 1; while (1) { while (R < c && _range(i, L, j, R) < k) ++ R; if (_range(i, L, j, R) < k) break; if (_range(i, L, j, R) >= k) ans = min(ans, (j-i+1)*(R-L+1)); ++ L; } } } printf("%d ", ans); } return 0; }
双指针拓展：
求区间M大数组成的数组中，第K大的数。