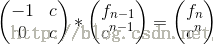数论:
快速乘:
ll ModMul(ll a,ll b,ll n){//快速积取模 a*b%n
ll ans=0;
while(b){
if(b&1)
ans=(ans+a)%n;
a=(a+a)%n;
b>>=1;
}
return ans;
}
快速幂:
ll ModExp(ll a,ll b,ll n){ //快速幂取模 a^b%n
ll ans=1;
while(b){
if(b&1)
ans=ModMul(ans,a,n);
a=ModMul(a,a,n);
b>>=1;
}
return ans;
}
Miller-Rabin素数检测算法:
bool miller_rabin(ll n){ ll i,j,a,x,y,t,u,s=10; if(n==2) return true; if(n<2||!(n&1)) return false; for(t=0,u=n-1;!(u&1);t++,u>>=1); //n-1=u*2^t for(i=0;i<s;i++){ a=rand()%(n-1)+1; x=ModExp(a,u,n); for(j=0;j<t;j++){ y=ModMul(x,x,n); if(y==1&&x!=1&&x!=n-1) return false; x=y; } if(x!=1) return false; } return true; }
素数筛(线性筛):

const ll maxn=100000001; ll prime[maxn]; //就是个素数表 bool sf[maxn]; //判断这个数是不是素数,sf[i]中的i是从1到maxn的数 void sushu() { //核心 欧拉筛代码 ll num=0; //num 用来记筛到第几个质数 memset(sf,true,sizeof(sf)); sf[1] = false; sf[0] = false; //1 0 特判 for(int i = 2;i <= maxn; i ++) { //外层枚举1~maxn if(sf[i]) prime[++num] = i; //如果是质数就加入素数表 for(int j = 1;j <= num;j ++) { //内层枚举num以内的质数 if(i * prime[j] > maxn) break; //筛完结束 sf[i * prime[j]] = false; //筛掉... if(i % prime[j] == 0) break; //避免重复筛 } } }
求前n个素数和与个数 O(n^(3/4)):

#include<bits/stdc++.h> using namespace std; typedef long long ll; ll check(ll v, ll n, ll ndr, ll nv) { return v >= ndr ? (n / v - 1) : (nv - v); } // ll S[10000000]; // ll V[10000000]; ll primenum(ll n) // O(n^(3/4)) { ll r = (ll)sqrt(n); ll ndr = n / r; assert(r*r <= n && (r+1)*(r+1) > n); ll nv = r + ndr - 1; std::vector<ll> S(nv+1); std::vector<ll> V(nv+1); for(ll i=0;i<r;i++) { V[i] = n / (i+1); } for(ll i=r;i<nv;i++) { V[i] = V[i-1] - 1; } for(ll i = 0;i<nv;i++) { S[i] = V[i] - 1; //求素数个数 } for(ll p=2;p<=r;p++) { if(S[nv-p] > S[nv-p+1]) { ll sp = S[nv-p+1]; // sum of primes smaller than p ll p2 = p*p; // std::cout << "p=" << p << ' '; // p is prime for(ll i=0;i<nv;i++) { if(V[i] >= p2) { S[i] -= 1LL * (S[check(V[i] / p, n, ndr, nv)] - sp);// //求素数个数 } else break; } } } return S[0]; } ll primesum(ll n) // O(n^(3/4)) { ll r = (ll)sqrt(n); ll ndr = n / r; assert(r*r <= n && (r+1)*(r+1) > n); ll nv = r + ndr - 1; std::vector<ll> S(nv+1); std::vector<ll> V(nv+1); for(ll i=0;i<r;i++) { V[i] = n / (i+1); } for(ll i=r;i<nv;i++) { V[i] = V[i-1] - 1; } for(ll i = 0;i<nv;i++) { S[i] = V[i] * ( V[i] + 1) / 2 - 1; //求素数和 } for(ll p=2;p<=r;p++) { // p is prime if(S[nv-p] > S[nv-p+1]) { ll sp = S[nv-p+1]; // sum of primes smaller than p ll p2 = p*p; for(ll i=0;i<nv;i++) { if(V[i] >= p2) { S[i] -= p* (S[check(V[i] / p, n, ndr, nv)] - sp); //求素数和 } else break; } } } return S[0]; } int main(int argc, char const *argv[]) { // std::cout << primesum(1e6) << ' '; std::cout << primenum(1e10) << ' '; std::cout << primesum(2e6) << ' '; cerr << "Time elapsed: " << 1.0 * clock() / CLOCKS_PER_SEC << " s. "; return 0; }
矩阵快速幂(嫖的):

struct Mat { LL m[101][101]; };//存储结构体 Mat a,e; //a是输入的矩阵,e是输出的矩阵 Mat Mul(Mat x,Mat y) { Mat c; for(int i=1;i<=n;++i){ for(int j=1;j<=n;++j){ c.m[i][j] = 0; } } for(int i=1;i<=n;++i){ for(int j=1;j<=n;++j){ for(int k=1;k<=n;++k){ c.m[i][j] = c.m[i][j]%mod + x.m[i][k]*y.m[k][j]%mod; } } } return c; } Mat pow(Mat x,LL y)//矩阵快速幂 { Mat ans = e; while(y){ if(y&1) ans = Mul(ans,x); x = Mul(x,x); y>>=1; } return ans; }
这里顺便再来几个常见的矩阵递推式:
1.f(n)=a*f(n-1)+b*f(n-2)+c;(a,b,c是常数)
2.f(n)=c^n-f(n-1) ;(c是常数)
3.f(n) = f(n-1)+f(n-2)
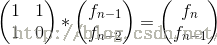
欧拉函数 求 一个数的因子有多少个(大数 10^18级)

#include <iostream> #include <algorithm> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <stack> #include <cstdlib> #include <iomanip> #include <cmath> #include <cassert> #include <ctime> #include <map> #include <set> using namespace std; #pragma comment(linker, "/stck:1024000000,1024000000") #define lowbit(x) (x&(-x)) #define max(x,y) (x>=y?x:y) #define min(x,y) (x<=y?x:y) #define MAX 100000000000000000 #define MOD 1000000007 #define pi acos(-1.0) #define ei exp(1) #define PI 3.1415926535897932384626433832 #define ios() ios::sync_with_stdio(true) #define INF 0x3f3f3f3f #define mem(a) (memset(a,0,sizeof(a))) typedef long long ll; const int s=8; char ch[26]; ll mult_mod(ll a,ll b,ll c) { a%=c; b%=c; ll ret=0; ll tmp=a; while(b) { if(b&1){ ret+=tmp; if(ret>c) ret-=c; } tmp<<=1; if(tmp>c) tmp-=c; b>>=1; } return ret; } ll pow_mod(ll a,ll n,ll mod) { ll ans=1; ll tmp=a%mod; while(n) { if(n&1) ans=mult_mod(ans,tmp,mod); tmp=mult_mod(tmp,tmp,mod); n>>=1; } return ans; } bool check(ll a,ll n,ll x,ll t) { ll ret=pow_mod(a,x,n); ll last=ret; for(int i=1;i<=t;i++) { ret=mult_mod(ret,ret,n); if(ret==1 && last!=1 && last!=n-1) return true; last=ret; } if(ret!=1) return true; else return false; } bool miller_pabin(ll n) { if(n<2) return false; if(n==2) return true; if((n&1)==0) return false; ll x=n-1; ll t=0; while((x&1)==0) {x>>=1;t++;} srand(time(NULL)); for(int i=0;i<s;i++){ ll a=rand()%(n-1)+1; if(check(a,n,x,t)) return false; } return true; } ll factor[110]; int tol=0; ll gcd(ll a,ll b) { ll t; while(b) { t=a; a=b; b=t%b; } if(a>=0) return a; else return -a; } ll pollard_rho(ll x,ll c) { ll i=1,k=2; srand(time(NULL)); ll x0=rand()%(x-1)+1; ll y=x0; while(1) { i++; x0=(mult_mod(x0,x0,x)+c)%x; ll d=gcd(y-x0,x); if(d!=1 && d!=x) return d; if(y==x0) return x; if(i==k){y=x0;k+=k;} } } void findfac(ll n,ll k) { if(n==1) return ; if(miller_pabin(n)) { factor[tol++]=n; return ; } ll p=n; ll c=k; while(p>=n) p=pollard_rho(p,c--); findfac(p,k); findfac(n/p,k); } int main() { ll n; scanf("%lld",&n); if(miller_pabin(n)) printf("2 "); else { findfac(n,107); ll ans=1; for(int i=0;i<tol;i++) { //printf("%lld ",factor[i]); ll pos=0; while(n>0 && (n%factor[i]==0)) { pos++; n/=factor[i]; } // printf("%lld %lld ",factor[i],pos); if(pos) ans*=(pos+1); } printf("%lld ",ans); } return 0; }
大数模板

//首先大数加法 两个大数相加 string sum(string s1,string s2) { if(s1.length()<s2.length()) { string temp=s1; s1=s2; s2=temp; } int i,j; for(i=s1.length()-1,j=s2.length()-1;i>=0;i--,j--) { s1[i]=char(s1[i]+(j>=0?s2[j]-'0':0)); //注意细节 if(s1[i]-'0'>=10) { s1[i]=char((s1[i]-'0')%10+'0'); if(i) s1[i-1]++; else s1='1'+s1; } } return s1; } //然后大数乘以整形数 string Multiply(string s,int x) //大数乘以整形数 { reverse(s.begin(),s.end()); int cmp=0; for(int i=0;i<s.size();i++) { cmp=(s[i]-'0')*x+cmp; s[i]=(cmp%10+'0'); cmp/=10; } while(cmp) { s+=(cmp%10+'0'); cmp/=10; } reverse(s.begin(),s.end()); return s; } //大数除以整形数 string Except(string s,int x) //大数除以整形数 { int cmp=0,ok=0; string ans=""; for(int i=0;i<s.size();i++) { cmp=(cmp*10+s[i]-'0'); if(cmp>=x) { ok=1; ans+=(cmp/x+'0'); cmp%=x; } else{ if(ok==1) ans+='0'; //注意这里啊。才找出错误 } } return ans; } //思想就是模拟乘法运算,用大数乘以另一个数的每一位然后大数相加就是ans string sum(string s1,string s2) //大数加法 { if(s1.length()<s2.length()) { string temp=s1; s1=s2; s2=temp; } int i,j; for(i=s1.length()-1,j=s2.length()-1;i>=0;i--,j--) { s1[i]=char(s1[i]+(j>=0?s2[j]-'0':0)); //注意细节 if(s1[i]-'0'>=10) { s1[i]=char((s1[i]-'0')%10+'0'); if(i) s1[i-1]++; else s1='1'+s1; } } return s1; } string Mult(string s,int x) //大数乘以整形数 { reverse(s.begin(),s.end()); int cmp=0; for(int i=0;i<s.size();i++) { cmp=(s[i]-'0')*x+cmp; s[i]=(cmp%10+'0'); cmp/=10; } while(cmp) { s+=(cmp%10+'0'); cmp/=10; } reverse(s.begin(),s.end()); return s; } string Multfa(string x,string y) //大数乘法 { string ans; for(int i=y.size()-1,j=0;i>=0;i--,j++) { string tmp=Mult(x,y[i]-'0'); for(int k=0;k<j;k++) tmp+='0'; ans=sum(ans,tmp); } return ans; } // string Multiply(string s,long x) //大数乘以整形数 { reverse(s.begin(),s.end()); long cmp=0; for(int i=0; i<s.size(); i++) { cmp=(s[i]-'0')*x+cmp; s[i]=(cmp%10+'0'); cmp/=10; } while(cmp) { s+=(cmp%10+'0'); cmp/=10; } reverse(s.begin(),s.end()); return s; } string Remove_later(string s) //删除一个字符串的后倒0 { int ok=1; for(int i=s.size()-1; i>=0; i--) { if(s[i]=='0'){ s.erase(i); } else if(s[i]=='.') { s.erase(i); ok=0; } else ok=0; if(ok==0) break; } return s; } string factorial(string s,int n) //浮点数的n次方 { if(n==0) return "1"; string cmp="",count=""; long x=0,point=0; for(int i=0; i<s.size(); i++) if(s[i]!='.') { cmp+=s[i]; x=x*10+(s[i]-'0'); } else point=s.size()-1-i; for(int i=1; i<n; i++) { cmp=Multiply(cmp,x); } int ans_point=cmp.size()-n*point; if(ans_point<0) { count+='.'; for(int i=ans_point; i!=0; i++) count+='0'; } string::iterator it=cmp.begin(); if(ans_point>=0&&ans_point<cmp.size()) cmp.insert(it+ans_point,'.'); count+=(Remove_later(cmp)); return count; } //字符串去除后导0函数,前导0可以先反转取后导。 string Remove_later(string s) //删除一个字符串的后倒0 { for(int i=s.size()-1; i>=0; i--) { if(s[i]=='0') s.erase(i); else break; } return s; }
O(N)找出没有重复的数 (异或,前提是其他数都出现了两次)

int find(int[] arr){ int tmp = arr[0]; for(int i = 1;i < arr.length; i++){ tmp = tmp ^ arr[i]; } return tmp; }
组合数打表(一)
原理:
空间:O(nm)
时间:预处理O(nm) 查询O(1)

for(int i=0;i<=n;i++){ c[i][0]=c[i][i]=1; for(int j=1;j<i;j++) c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod; }
(二)
原理:费马小定理
空间:O(n)
时间:预处理O(n) 查询O(log p)

ll qpow(ll a,ll b){ ll ans = 1,base = a; while(b){ if(b&1) ans = ans * base % mod; base = base * base % mod; b>>=1; } return ans; } void init(){ f[0]=1; for(int i=1;i<=2e5;i++){ f[i]=f[i-1]*i%mod; } } ll C(ll n,ll m){ if(n<m) return 0; return 1ll*f[n]*qpow(f[m],mod-2)%mod*qpow(f[n-m],mod-2)%mod; }
(三)lucas

#define int long long int t,n,m,p,f[100005]; int pow(int x,int y,int p){ //快速幂 x%=p; int ans=1; for(int i=y;i;i>>=1,x=x*x%p) if(i&1) ans=ans*x%p; return ans; } int C(int n,int m,int p){ //求组合数 if(m>n) return 0; return ((f[n]*pow(f[m],p-2,p))%p*pow(f[n-m],p-2,p)%p); } int lucas(int n,int m,int p){ //Lucas定理 if(!m) return 1; return C(n%p,m%p,p)*lucas(n/p,m/p,p)%p; } signed main(){ scanf("%d",&t); while(t--){ scanf("%d%d%d",&n,&m,&p); f[0]=1; for(int i=1;i<=p;i++) f[i]=(f[i-1]*i)%p; printf("%lld ",lucas(n+m,m,p)); } }