【2018-2019 ACM-ICPC, Asia Jiaozuo Regional Contest】F.Honeycomb

蜂窝是由蜜蜂构建的块状蜡单元，可以描述为欧几里得平面的规则平铺，其中三个六边形在每个内部顶点相交。六边形的内角为120度，因此一个点上的三个六边形成360度。下图显示了具有3行4列的完整蜂窝。

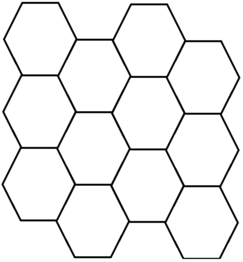
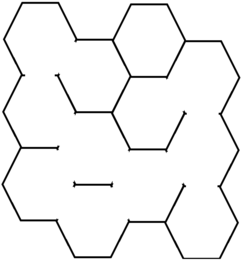
在这里，我们保证第二列中的第一个单元格始终位于第一列中第一个单元格的右下角，如上所示。在完整的蜂窝基础上，普通蜂窝可能会丢失相邻单元之间的某些壁，但蜂窝仍处于封闭状态。可能的情况如下图所示。

汉密尔顿（Hamilton）是生活在普通蜂窝中的勇敢蜂。现在，他想从起点移动到指定的目的地。下图给出了从第2列的第一个单元格到第4列的第一个单元格的3×4蜂窝状的可行路径。

请帮助他找到从指定起点到目的地的可行路径必须经过的最小单元数（包括起点和终点）。

 

Input

输入包含多个测试用例，第一行包含一个正整数T，表示测试用例的数量，最多为10^4 。 对于每个测试用例，第一行包含两个整数r 和c表示蜂窝的行数和列数，其中2≤r，c≤10^3 。 以下（4r + 3） 行描述了整个给定的蜂窝，其中每行最多包含（6c + 3）个字符。奇数线包含以加号（“ +”）和零个或多个水平边缘表示的网格顶点，而偶数线包含两个或多个对角边缘。具体来说，一个单元格描述为6个顶点，最多6个顶点 边缘。它的上限或下限表示为三个连续的负号（“-”）。它的对角线边缘中的每一个（如果存在）都是单个正斜杠（“ /”）或单个反斜杠（“ ”）字符。所有边缘字符将精确地放置在相应的顶点之间。在起始单元格的中心（代表目的地），使用大写字母“ S”（代表大写字母“ T”）作为特殊字符来表示特殊单元格。所有其他字符将为空格字符。注意，如果任何输入行可能包含尾随空格，则将省略该空格。 我们保证所有最外壁都存在，从而使给定的蜂窝关闭，并且在给定的蜂窝中恰好出现一个“ S”和一个“ T”。此外，r⋅c之和 在所有测试用例中，最大为2×10^6。104

Output

对于每个测试用例，输出一行，其中包含汉密尔顿从起始单元格（“ S”）到目的地（“ T”）到起始位置（包括起始单元格和目标位置）所需的最少单元格数量。如果不存在可行路径，则输出-1。

Example

Input

1
3 4
  +---+       +---+
 /          /     
+       +---+       +---+
                 /     
  +   +   S   +---+   T   +
 /          /           /
+       +---+       +   +
                 /     
  +---+       +---+       +
 /                       /
+       +---+       +   +
                  /     
  +---+       +---+       +
            /          /
        +---+       +---+

Output

7

不得不说的是这题真的是很恶心啊，居然卡memset，TLE到怀疑人生，知道看了网上的题解才知道不能memset。
之后这道题就是一比较简单的迷宫模拟而已，所改变的就是前进的步数而已。
然后这道题比较重要的地方是需要判断走半步能不能走，就是会不会遇到墙壁。然后就没啥好说的了。
以下是AC代码：

#include <bits/stdc++.h>
using namespace std;
struct node
{
    int x, y;
    int step;
}st;
const int maxn = 1e3 + 10;
int dic[6][2] = {1,3, 1,-3, -1,3, -1,-3, 2,0, -2,0};
char s[maxn*6][maxn*6];
bool vis[maxn*6][maxn*6];
int n, m;
int solve()
{
    queue <node> q;
    node temp, cur;
    vis[st.x][st.y] = true;
    q.push(st);
    while (!q.empty())
    {
        cur = q.front();
        q.pop();
        if (s[cur.x][cur.y] == 'T')
            return cur.step;

        for (int i = 0; i < 6; i++)
        {
            temp.x = cur.x + dic[i][0],
            temp.y = cur.y + dic[i][1],
            temp.step = cur.step + 1;

            if (temp.x > 0 && temp.x < 4*n+3 && temp.y > 0 && temp.y < 6*m+3
                && s[temp.x][temp.y] == ' ')
            {
                temp.x += dic[i][0], temp.y += dic[i][1];
                if (vis[temp.x][temp.y]) 
                    continue;
                vis[temp.x][temp.y] = true;
                q.push(temp);
            }
        }
    }
    return -1;
}


int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        scanf("%d %d", &n, &m);
        getchar();
        for (int i = 0; i < 4*n+3; i++)
        {
            gets(s[i]);
            int len = strlen(s[i]);
            for (int j = 0; j < len; j++)
                if (s[i][j] == 'S')
                    st.x = i, st.y = j, st.step = 1;
        }
        printf("%d
", solve());
        for(int i = 0; i < 4 * n + 3; i++){
            int len = strlen(s[i]);
            for(int j = 0; j < len; j++){
                s[i][j] = '';
                vis[i][j] = false;
            }
        }
    }
    return 0;
}