一、引入
空间域方法：对像素操作的过程->对图像像素直接处理。
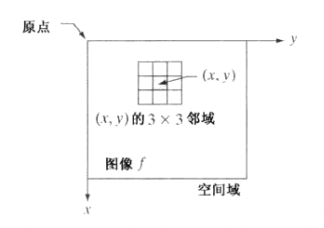
空间域处理可由该式定义： (g(x,y)=T[f(x,y)])
其中，f(x,y)为原图像，g(x,y)为处理后的图像，T为定义在x,y的邻域（不一定是4/8/m邻域，可能是更大的范围，如3x3，5x5的mask,et al）内的一个操作（也叫做算子）。
最小邻域的大小为1x1，在这种情况下，g(x,y)仅取决于对应的f(x,y)值，上式可变换为一个形如下式的灰度（级）变换函数/灰度映射函数： (s=T(r)) 其中，r和s分别为g和f在(x,y)的灰度。
当处理原点位于图像边界时，部分邻域将位于图像外部，此时要么忽略外部邻点，要么用0填充灰度图像边缘，被填充边界的厚度取决于邻域的大小。
二、基本灰度变换
由于曝光不足/成像设备的非线性/图像记录设备动态范围太窄等因素，会产生对比度不足的弊病，使图像细节难以分辨，可以使用灰度变换解决这些问题。灰度变换的实质是邻域的1x1的图像变换（点运算）。
线性灰度变换
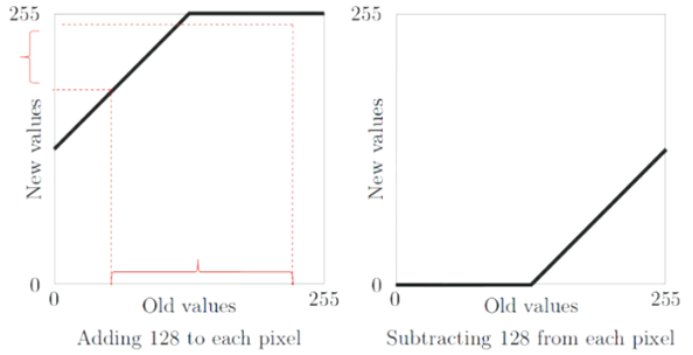
1.加减常数（等价于提高/降低亮度）
(g(x,y)=f(x,y) pm C)
作用：压缩动态范围，降低对比度。
以下是一个例子：
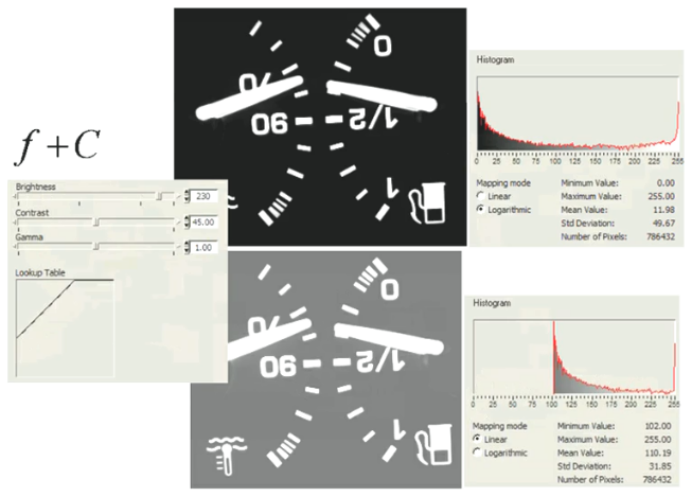
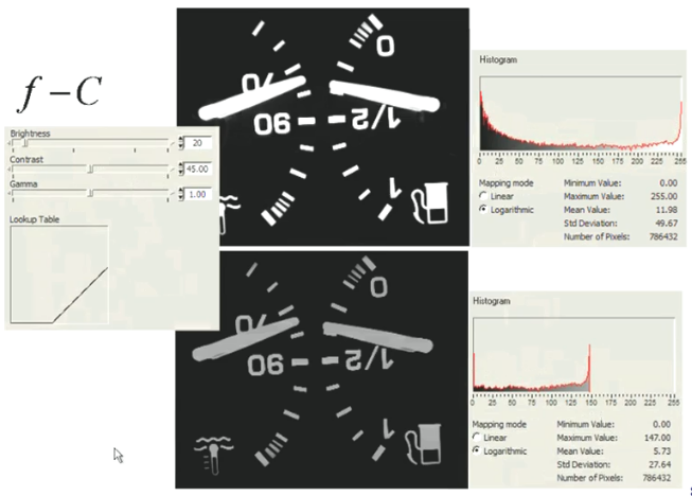
图像反转
图像反转是线性变换-加减常数中的一个简单变换。
在matlab中可以使用b=imcomplement(a)来反转图像。
(如果灰度为256级（0-255），可以写作g(x,y)=255-f(x,y))
(更一般地，可以写作s=L-1-r或者g(x,y)=L-1-f(x,y)，其中L-1为灰度最大级)
变换函数如下：
效果如下：
2.乘常数
(g(x,y)=C imes f(x,y))
作用：改变动态范围
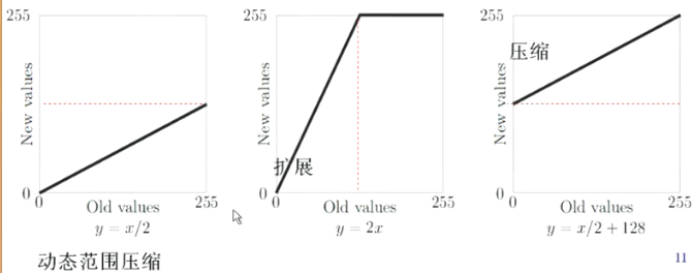
一些examples：
线性灰度变换的一般表达式：
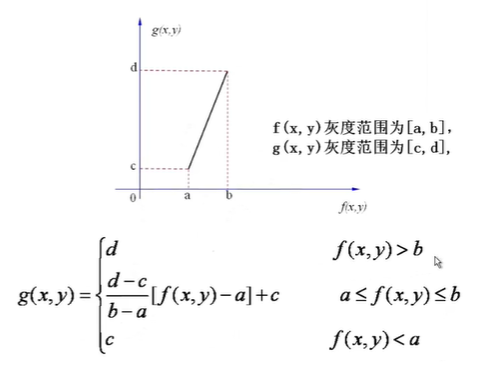
分段线性函数
可以将感兴趣的灰度范围线性拓展，相对抑制不感兴趣的灰度区域。
- 对比度拉伸
对比拉伸是最简单的分段线性函数，对比拉伸的思想是提高图像处理是灰度级动态范围。（低对比度->高对比度）
一个极端的例子是二值变换，超过therhold输出1，否则0.
- 灰度切割/灰度窗口变换
def：提高图像中特定灰度范围的亮度的方法。
方法1：将所关心范围内灰度设定为较高值，其他灰度值设为较低值。
方法2：使所需范围的灰度变量，而保持其他区域的灰度色调。
- 位图切割
def：对特定位提高亮度。
假设每个像素位深度为8（0-255），可以将每位对应的图像平面分离出来
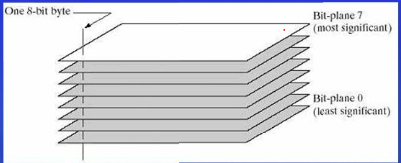
感觉就是以对应位的1来做阈值得到每一位阈值对应的新图像。
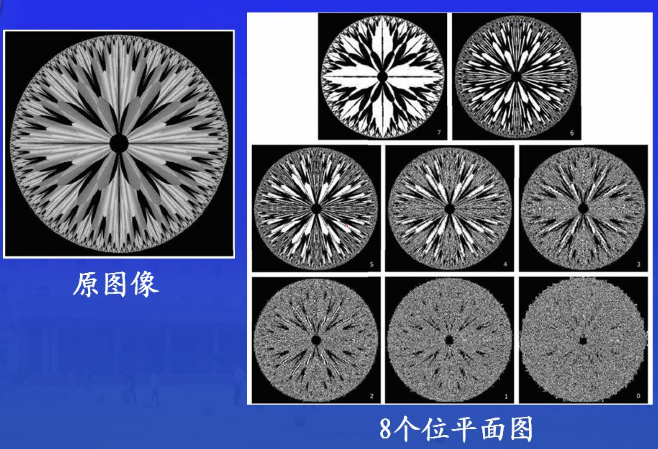
对数变换
(s=c imes log(1+r))
其中c为一个常数，并假如r≥0，扩大了窄带低灰度输入图像的输出范围，可以用这种变换来拓展被压缩的高值图像中的暗像素。压缩动态范围
需要对新图像灰度级重新标定/量化，使用：
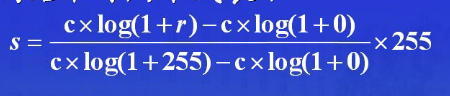
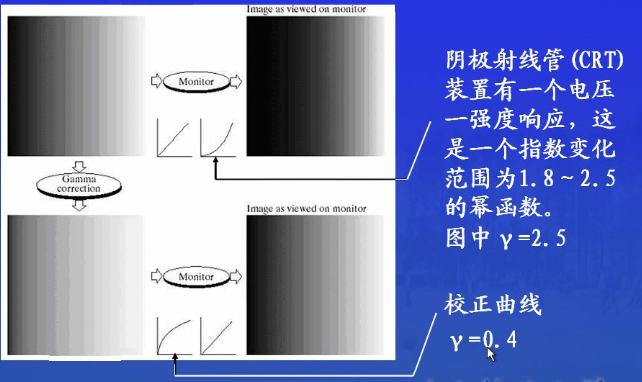
Gamma变换/幂次变换
(s=c imes r^gamma)
(gamma小于1和大于1的值的曲线会产生相反的效果)
小于1时拉伸原图像低灰度值部分到更宽的范围
大于1时拉伸原图像高灰度值部分到更宽的范围
(幂次变换也叫gamma校正，用来校正监视器显示的非线性特点。)
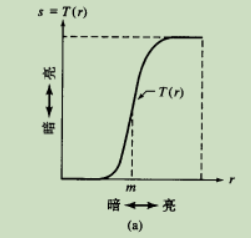
对比度拉伸变换
对比度变换是一种通过改变图像像元的亮度值来改变图像像元的对比度，从而改善图像质量的图像处理方法。因为亮度值是辐射强度的反应，所以也称为辐射增强。
原理：将图像中过于集中的像元分布区域（亮度值分布范围）拉开扩展，扩大图像反差的对比度，增强图像表现的层次性。达到增强反差的目的，主要通过调整直方图来实现。
函数图像类似于下图，其中r为输入图像的亮度，s为输出图像亮度，斜率由参数E控制，中点由参数m控制：
三、直方图处理
图像的灰度直方图是最简单最有用的工具之一。
直方图：表示数字图像中每一灰度级像素出现的频次。（该灰度级的像素数目）
可表示为： (p(k)=n_k) (n_k) 是图像中第k个灰度级的像素总数
或 (p(r_k)=n_k/n) n是图像的像素总数。（概率密度表示）
灰度直方图的性质：
- 无空间信息
- 直方图与图像一对多关系
- 可叠加性（整幅图像的直方图可由子图像的直方图叠加得到）
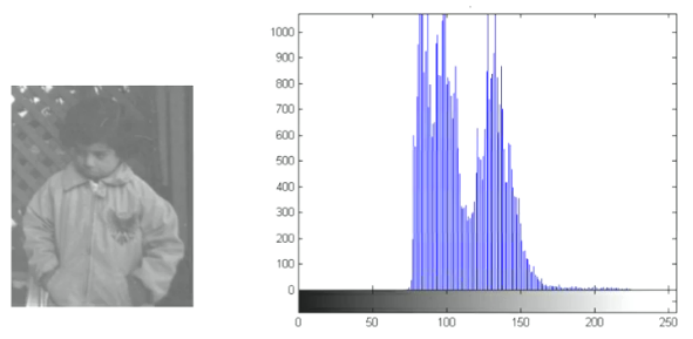
以上图为例，图像中间灰度及像素多，动态范围小，图像对比度低。
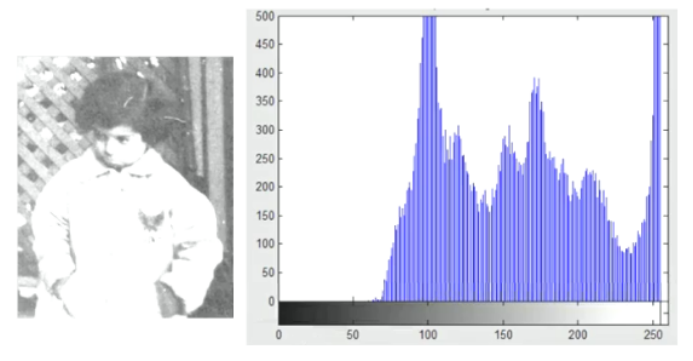
高灰度的像素占了绝大部分，图像偏亮。
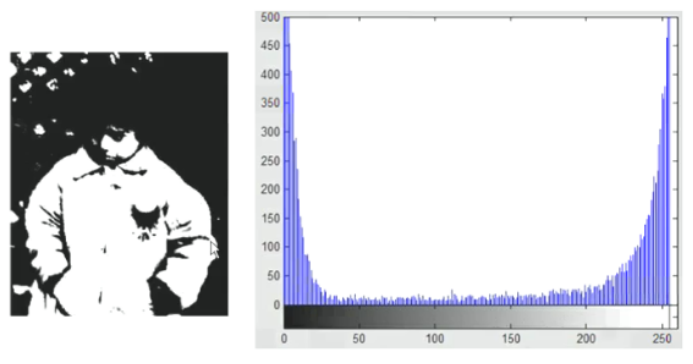
过低、过高灰度级的像素占了绝大部分，对比度过大，类似于二值图像。
直方图反映了图像的清晰程度，直方图均匀分布时，图像最清晰。（判断一幅图像是否清晰->是否充分利用了尽可能多的灰度等级）
直方图均衡
直方图修正：通过灰度映射函数T将原灰度直方图转化为希望得到的直方图。
直方图均衡与直方图规定化（匹配）的区别在于一个得到灰度较为均衡的图像一个得到与规定直方图灰度近似的图像。
(G_{new}=T(G_{old}))
直方图均衡是最常用的直方图修正，即将给定图像的直方图改造成均匀直方图分布。
均匀化后，图像直方图是平直的，即各个灰度级具有相同的出现频数，或各灰度级具有均匀的概率分布，得到更清晰的图像（图像增强）
直方图均衡化灰度映射函数
连续灰度级情况
(P(r):概率密度函数，0（黑）≤r≤1（白），代表灰度级)
找到一种变换函数 (s=T(r))，使直方图变平直。
为使变换后的灰度仍保持从黑到白的单一变化顺序，且变换范围与原先一致，以避免整体变亮或变暗。
规定：
1.(在0≤r≤1(L-1)中，T(r)是单调递增函数，且0≤T(r)≤1，保证灰度变换前后不倒置。)
2.(反变换r=T^{-1}(s),T^{-1}为单调递增函数（不知道怎么来的），0≤s≤1(L-1)。保证变换后灰度值仍在变换前允许的灰度级范围内。)
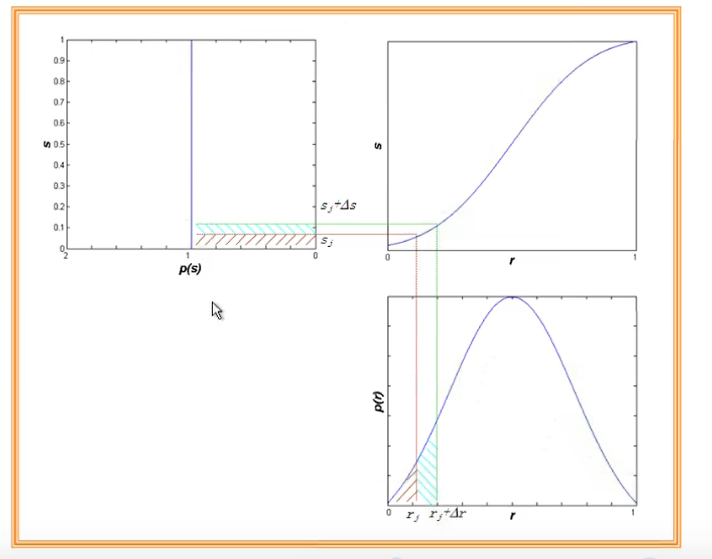
可以看到r较小时变换函数斜率也小，较大一段才能转换为灰度范围较小的灰度，而中间一段斜率很大，微小的一段也能转换为较大灰度范围内的值（分布）（非线性变换，与图内情况匹配）
对于变换函数:
其中右侧是r的累计分布函数，将其代入
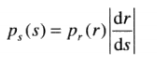
可得到
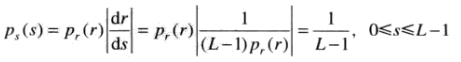
即s的概率密度分布是均匀分布的（如果s的上限为1则密度为1）
数字图像（离散）的直方图均衡
设一幅数字图像的像素总数为n,分为L个灰度级。
第k个灰度级出现的概率：
(p_r(r_k)=n_k/n,其中n_k为第k个灰度级的频数，r_k为原图像第k灰度级的值。可归一化为0~1。n为像素总数。k=0,1，...，L-1.L为可能的灰度级数量。)
对应变换的离散形式为：
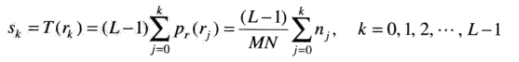这里L-1是因为上限值为L-1，归一化后可写为1.
根据概率密度函数乘L-1（最大灰度级）后向下取整得到的灰度值归类。
性质：
- 与连续形式不同，一般不能证明离散变换能产生均匀概率密度函数的离散值。（事实上大多数时候都不能）
- 直方图均衡化具有完全自动化的特点。
- 结果图像的灰度级与原图像一致。
直方图匹配
某些应用使用直方图均衡进行基本增强的方案不合适，如下：
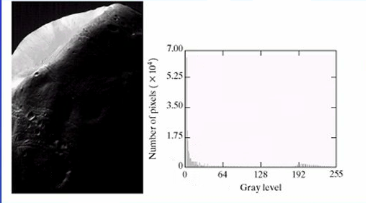
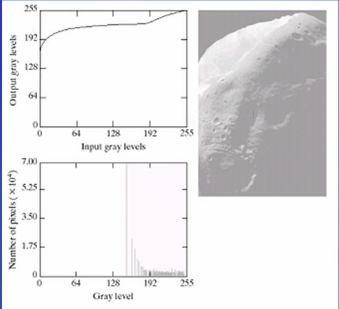
通过规定输出直方图的灰度分布，可以得到相较令人满意的结果。
(设从r->z映射，计算每个r_j对应的s_j=T(r);计算每个z_j对应的v_j=G(z)；对每一个s_j寻找最接近的v_k，该v_k对应的z_k就是r_j应该映射为的灰度值。最后得到的灰度直方图与规定的直方图类似（很好理解，离散情况下肯定是近似）。)
凑就嗯凑
局部处理
1.应用直方图进行局部增强
局部直方图均衡：对mask里的所有像素求直方图均衡
直方图统计
(令r表示在[0,L-1]上代表离散灰度的离散随机变量，令p(r_i)代表对应r的第i个值的归一化直方图分量，可以把p(r_i)看作灰度级r_i出现的概率估计值。)r的平均值为(m=sum_{i=0}^{L-1}r_ip(r_i))
r的方差（二阶矩,对比度的衡量）为：
(mu_2(r)=sum_{i=0}^{L-1}(r_i-m)^2p(r_i)=sigma^2(r))
局部均值(平均灰度值）/方差（对邻域对比度的衡量）：
(m_{s_{xy}}=sum_{i=0}^{L-1}r_ip_{s_{xy}}(r_i))
(sigma^2_{s_{xy}}=sum_{i=0}^{L-1}(r_i-m_{s_{xy}})^2p_{s_{xy}}(r_i))
四、空域滤波
基本原理
对待处理图像逐点移动掩模。简单来说就是在mask的邻域中对实际像素值乘模板值再求和。
线性滤波与卷积类似，因此mask也称为卷积模板/卷积核。
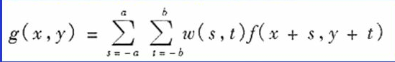
对n*n的mask，当掩模中心与图像边缘小于等于(n-1)/2个像素时，就会有图像之外的值。处理方法如下：
1.不对边上(n-1)/2个像素操作，结果会得到比原图像小的图，可以将未处理的图像的边缘像素复制到结果图像，再对边缘的像素带使用部分滤波掩模处理。
2.对边界的(n-1)/2行和列补上灰度为0的像素。（黑边）或者将边缘复制补在图像之外。
平滑滤波器
平滑滤波器用于模糊处理/减小噪声。经常用于预处理。
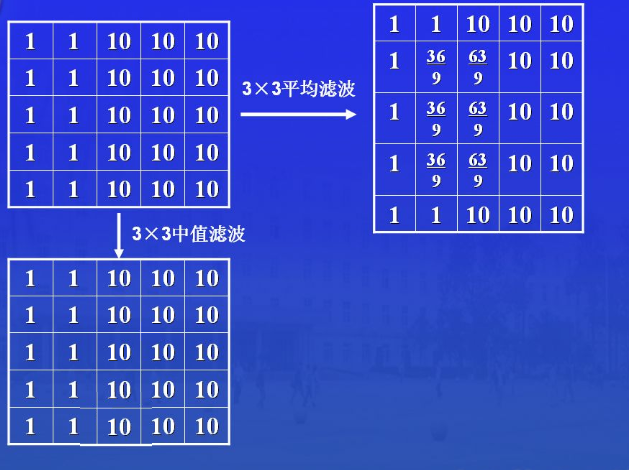
平滑线性滤波器
平滑线性滤波器的响应是在mask邻域内像素的加权平均值。因此，也被称为均值滤波器。
由于图像边缘是由图像灰度尖锐变化带来的特性，所以均值滤波处理会带来边缘模糊。
统计排序滤波器
统计滤波器是一种非线性的空间滤波器，响应基于滤波器包围的图像区域中像素的派速，然后由统计排序结果决定的值替代中心像素值。常见的例子是中值滤波器
中值滤波器是将像素邻域内灰度的中值（中位数）代替该像素的值。
比小尺寸的线性平滑滤波器的模糊程度明显要低。
锐化滤波器
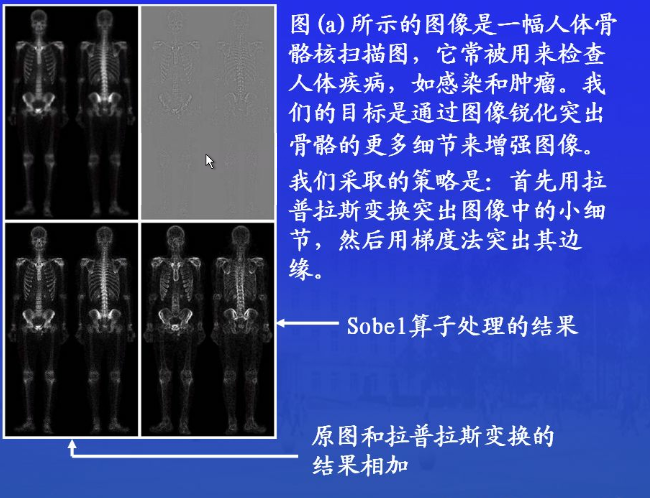
锐化处理的目的是为了突出图像的细节或增强被模糊的细节。
锐化处理可以通过空间微分来完成。微分算子的响应强度与图像在该点的突变程度有关，增强了边缘和其他突变（噪声）并削弱了灰度变化缓慢的区域。
用差分定义二阶微分：
其中
1.在平坦区域微分为0
2.在斜坡的起始点微分非零
3.沿着斜坡面的微分值为0
首先定义一个二阶微分的离散公式，然后构造一个基于此式的滤波器，需要各向同性滤波器，这种滤波器的响应与滤波器作用的图像的突变方向无关。（对各方向都检测？）
基于二阶微分的图像增强————Laplace算子
连续上的定义：
在x方向上的二阶偏微分如下：
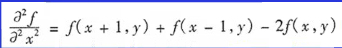
对y同理。
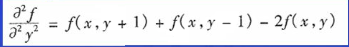
二者相加得到二阶拉普拉斯算子：
二阶拉普拉斯算子的四种形式：
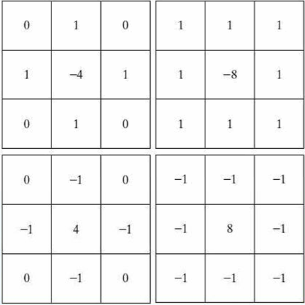
左一：直接推导的模板（以90°旋转的各向同性）
右一：增加了对角线方向
左二及右二：上边两个的变形。
基于一阶微分的图像增强————梯度法
梯度的定义：
梯度的模由下式给出：
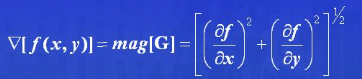
梯度向量本身是线性算子，但它的模用到了平方和开方运算。一般将梯度的模称为梯度算子。
常常用绝对值代替平方/开方近似求梯度的模。
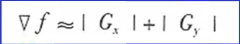
将模板中心看作f(x,y)对x和y求微分。
Robert算子
提出新的定义计算微分：
对应的算法和mask形式为：
偶数尺寸的mask并不好用，为了得到3x3最小滤波器mask，对上式的近似为：
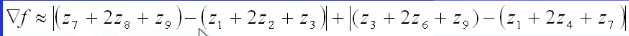
mask形式为：
混合空间增强
使用多种互补的图像增强技术，一个例子：
