OpenMesh 提供了许多可供使用的向量操作函数,使用特别方便。
计算距离:
从官方文档可以看到OpenMesh提供了5个函数,分别为
Scalar length() const //compute euclidean norm
Scalar norm() const //compute euclidean norm
Scalar sqrnorm() const //compute squared euclidean norm
Scalar l1_norm() const //compute L1 (Manhattan) norm
Scalar l8_norm() const //compute l8_norm
test:
MyMesh::Normal p(1,-1,2), q(0,1,3); cout<<"length : "<<(p-q).length()<<endl; cout<<"norm : "<<(p-q).norm()<<endl; cout<<"sqrnorm : "<<(p-q).sqrnorm()<<endl; cout<<"l1_norm : "<<(p-q).l1_norm()<<endl; cout<<"l8_norm : "<<(p-q).l8_norm()<<endl;
result:
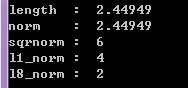
对于二维空间上的点(也可看做向量,起点为原点) p(x1,y1), q(x2,y2)
欧几里得距离 norm =( (x2-x1)2 + (y2-y1)2 )½
曼哈顿距离(L1距离) l1_norm = |x2-x1| + |y2-y1|
切比雪夫距离(L∞距离) l8_norm = max{|x2-x1| , |y2-y1|}
max & min
test:
1 MyMesh::Normal p(1,-3,2), q(0,2,4); 2 cout<<"max : "<<p.max()<<endl; 3 cout<<"max_abs : "<<p.max_abs()<<endl; 4 5 cout<<"maximize : "<<p.maximize(q)<<endl; 6 cout<<p<<endl<<q<<endl; 7 cout<<"maximized : "<<p.maximized(q)<<endl; 8 cout<<p<<endl<<q<<endl; 9 cout<<"maximized : "<<q.maximized(p)<<endl; 10 cout<<p<<endl<<q<<endl;
result:
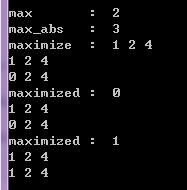
从result来看,max 和 max_abs 很简单,不用多说。对于 p.maximize(q) 返回值是向量p与q对应位置的最大值组成的向量,而 p.maximized(q) 判断向量p是否经历了maximize,返回值为0则向量p不变,未经过maximize, 返回值为1则向量p改变,即经过maximize。
对于min,有同样的操作,不再赘述。
向量单位化
OpenMesh提供了三个单位化的函数
vector type & normalize() //normalize vector, return normalized vector
const vector type normalized() //return normalized vector
vector type & normalize_cond() //normalize vector, return normalized vector and avoids div by zero
外加单位化的定义(长度为1),有四种单位化方法。
test:
1 MyMesh::Normal p1(1,-3,2), p2(1,-3,2), p3(1,-3,2), p4(1,-3,2); 2 3 MyMesh::Normal q1 = p1.normalize(); 4 cout<<"p1 : "<<p1.length()<<" "<<p1<<endl; 5 cout<<"q1 : "<<q1.length()<<" "<<q1<<endl<<endl; 6 7 MyMesh::Normal q2 = p2.normalized(); 8 cout<<"p2 : "<<p2.length()<<" "<<p2<<endl; 9 cout<<"q2 : "<<q2.length()<<" "<<q2<<endl<<endl; 10 11 MyMesh::Normal q3 = p3/(p3.length()); 12 cout<<"p3 : "<<p3.length()<<" "<<p3<<endl; 13 cout<<"q3 : "<<q3.length()<<" "<<q3<<endl<<endl; 14 15 MyMesh::Normal q4 = p4.normalize_cond(); 16 cout<<"p4 : "<<p4.length()<<" "<<p4<<endl; 17 cout<<"q4 : "<<q4.length()<<" "<<q4<<endl<<endl<<endl;
result:

从结果看出,1和4效果一样,1和2效果不同,需要注意!!!
点乘叉乘(内积外积)
test:
1 MyMesh::Normal p(1,-3,2), q(0,2,4); 2 cout<<"dot product : "<< (p | q) <<endl; 3 cout<<"cross product : "<< (p % q) <<endl;
result:

向量 p(x1,y1,z1), q(x2,y2,z2)
点乘(内积):x1*x2 + y1*y2 + z1*z2
叉乘(外积):(y1*z2-y2*z1, x2*z1-x1*z2, x1*y2-x2*y1) (来自行列式表示的化简,cnblog不能打公式么???)