分治法
把大问题化成小问题逐个解决,可以优化算法复杂度(局部的优化有利于全局,一个问题的解决,其影响力扩大了k倍,即扩大到了全局)。
- 归并排序
(1)分解:把原来无序的数列分成两部分,对每个部分再继续分解成更小的两部分,直到子序列只包含1个数,这个过程用递归实现(在归并排序中,只是简单地把数列分成两半,在快速排序中,是把序列分成左右两部分,左部分元素都小于右部分的元素)
(2)求解子问题。
(3)合并:合并两个有序的子序列。
和交换排序相似,但合并两个有序的子序列是有序的,因此效率更高。
归并排序的时间复杂度为O(nlog2n),空间复杂度为O(n)。
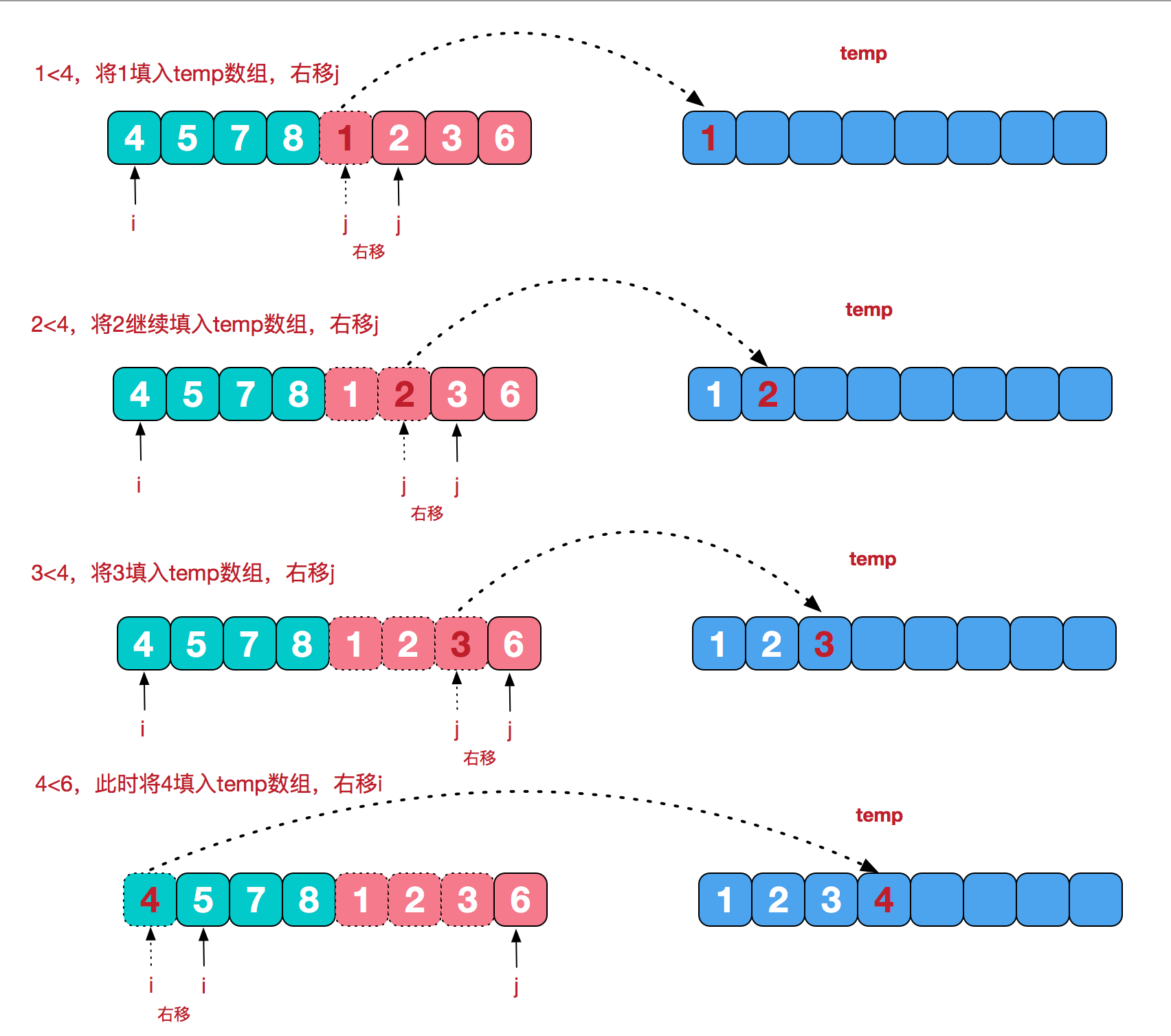
图解释得很清楚,就是比较两个子序列,得到的数存到另一个数组里。(とても簡単です)
排序是竞赛中的常用功能,一般直接使用STL的sort()函数,并不需要自己再写一个排序的程序。不过也有一些特殊的问题,需要写出程序,并在程序内部做一些处理,例如逆序对问题。
放题:http://acm.hdu.edu.cn/showproblem.php?pid=4911

k=0直接暴力求有多少个逆序对,然后你就快快乐乐地TLE了。
![]()
在子序列里元素都是有序的,不存在逆序对,逆序对只存在于不同的子序列之间。
如果前一个子序列元素比后面元素大,就会产生逆序对。(注意产生的逆序对个数不止一个:cnt+=mid-i+1)
在所有相邻数中,只有交换那些逆序的才会影响逆序对的数量。设原始序列有cnt个逆序对:
当k不等于0时,又分两种情况:
(1)cnt<=k,总逆序对交换次数<k,那么最少的逆序对数量为0.
(2)cnt>k,k次交换都发生在逆序的相邻数上,那么剩余的逆序对是cnt-k。
放代码:
#include<iostream> #include<algorithm> using namespace std; const int N=1e5+5; typedef long long ll; ll a[N],b[N],cnt; void merge(ll l,ll mid,ll r){ ll i=l,j=mid+1,t=0; while(i<=mid&&j<=r){ if(a[i]>a[j]){ b[t++]=a[j++]; cnt+=mid-i+1; } else b[t++]=a[i++]; } while(i<=mid){ b[t++]=a[i++]; } while(j<=r){ b[t++]=a[j++]; } for(i=0;i<t;i++){ a[l+i]=b[i]; } } void mergesort(ll l,ll r){ if(l<r){ ll mid=(l+r)>>1; mergesort(l,mid); mergesort(mid+1,r); merge(l,mid,r); } } int main(){ ll n,k; while(~scanf("%lld%lld",&n,&k)){ cnt=0; for(ll i=0;i<n;i++){ scanf("%lld",&a[i]); } mergesort(0,n-1); if(cnt<=k) printf("0 "); else printf("%I64d ",cnt-k); } return 0; }
逆序对除了可以用归并,还可以用树状数组求解......这个东西就放在以后再说吧!
- 快速排序
把序列分为左右两部分,使左边所有的数都小于右边的数,递归,直到不能再分为止。定一个基准数t,若a[i]>=a[t],i++。若a[i]<a[t],交换a[i]和a[j],然后i++,j++,最后交换a[j]和a[t],得到结果。
补充:关于快排不稳定的问题
快排的每一次划分都把序列分成了左右两部分,在这个过程中,需要比较所有的元素,有O(n)次。如果每次划分都是对称的,也就是说左右两部分长度差不多,那么一共需要划分O(log2n)次。总复杂度为O(nlog2n)。
如果划分不是对称的,左部分和右部分的数量差别很大,那么复杂度就会高一些。比如左部分只有一个数,剩下的数都在右部分,那么最多可能划分n次,总复杂度是O(n^2)。所以快速排序是不稳定的。当测试数据故意卡快排的极端情况,例如测试数据是100000个完全一样的数字,就会超时了。
不过一般情况下快速排序效率很高,甚至比稳定的归并排序更好。
应用:求第k大数问题,递归包含第k个数的那部分就行了。
练习题:
https://www.luogu.com.cn/problem/P1177
http://acm.hdu.edu.cn/showproblem.php?pid=1425求前k大的数
http://poj.org/problem?id=2388求中间数
(sort用法之前的博客已经写过咯)
EOF