Problem Description
A thief is running away! We can consider the city where he locates as an undirected graph in which nodes stand for crosses and edges stand for streets. The crosses are labeled from 0 to N–1. The tricky thief starts his escaping from cross S. Each moment he moves to an adjacent cross. More exactly, assume he is at cross u at the moment t. He may appear at cross v at moment t + 1 if and only if there is a street between cross u and cross v. Notice that he may not stay at the same cross in two consecutive moment. The cops want to know if there’s some moment at which it’s possible for the thief to appear at any cross in the city.
Input
The input contains multiple test cases: In the first line of the input there’s an integer T which is the number of test cases. Then the description of T test cases will be given. For any test case, the first line contains three integers N (≤ 100 000), M (≤ 500 000), and S. N is the number of crosses. M is the number of streets and S is the index of the cross where the thief starts his escaping. For the next M lines, there will be 2 integers u and v in each line (0 ≤ u, v < N). It means there’s an undirected street between cross u and cross v.
Output
For each test case, output one line to tell if there’s a moment that it’s possible for the thief to appear at any cross. Look at the sample output for output format.
Sample Input
2 3 3 0 0 1 0 2 1 2 2 1 0 0 1
Sample Output
Case 1: YES Case 2: NO
Hint
For the first case, just look at the table below. (YES means the thief may appear at the cross at that moment)
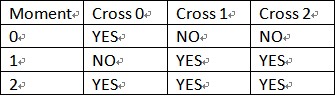
For the second input, at any moment, there’s at least one cross that the thief can’t reach.
Source
转自别人的解释:
如果出现遍历图中的某个点都是在奇数时刻或者偶数时刻,那么小偷的藏点就是根据时间判定在某些的奇数点和偶数点了。
如果图出现奇数的环,即:有一个环由奇数个点组成,那么环中的某个点在奇数和偶数时刻都能到达(可以画图试试)。其实奇数环导致小偷藏点无规律的最大原因是:
在遍历最后奇数环的两个(必定是两个)未遍历点的时候他们是同奇(偶)的,然而还有一条边直接相连。导致在下一时刻,那两个点又可以同时变成偶(奇)。如果在回溯遍历的话,就会出现整张图在奇数时刻或者偶数时刻都能到达。
无向图G为二部图的充分必要条件是:
G至少有两个顶点,且其所有回路的长度均为偶数。
如果我们把图中奇数时刻能够到达的点归到X集合,偶数能到点归到Y集合,那么如果图中出现相同集合的点有
边相连,那么就不满足二分图的性质,即可输出YES,如果原图可二分图话,答案就是NO了。
然后就是经典的二分图判定。
///
题意:一个小偷从初始点逃到他相邻的点,从某个点到另外若干个相邻的点的时间是相同的,
也就是同个时间点,问你在同个时间点小偷能否遍历全部点,能的话输出YES,否则输出NO。
解法:DFS判断连通性+DFS染色判断是否为二分图。
如果是个二分图那么它的奇数步和偶数步是属于各自独立的集合,
如果奇数步能够遍历到偶数步,这个意思就是此小偷可以在某个时间点遍历整个图的点。
画个奇数点的环,从某个点出发一点存在一条边,同时改变改点的奇偶性。
///
总之,只要判断连通性和二分图即可
bfs实现染色:

1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<cmath> 6 #include<math.h> 7 #include<algorithm> 8 #include<queue> 9 #include<set> 10 #include<bitset> 11 #include<map> 12 #include<vector> 13 #include<stdlib.h> 14 #include <stack> 15 using namespace std; 16 #define PI acos(-1.0) 17 #define max(a,b) (a) > (b) ? (a) : (b) 18 #define min(a,b) (a) < (b) ? (a) : (b) 19 #define ll long long 20 #define eps 1e-10 21 #define MOD 1000000007 22 #define N 100006 23 #define inf 1e12 24 25 //////////////////////////////////////////////////// 26 int fa[N]; 27 void init(){ 28 for(int i=0;i<N;i++){ 29 fa[i]=i; 30 } 31 } 32 int find(int x){ 33 return fa[x]==x?x:fa[x]=find(fa[x]); 34 } 35 bool merge(int x,int y){ 36 int root1=find(x); 37 int root2=find(y); 38 if(root1==root2) return false; 39 fa[root1]=root2; 40 return true; 41 } 42 /////////////////////////////////////////////////// 43 int n,m,s; 44 vector<int> v[N]; 45 int color[N]; 46 bool bfs(){ 47 queue<int>q; 48 q.push(s); 49 color[s]=0; 50 while(!q.empty()){ 51 int t1=q.front(); 52 q.pop(); 53 54 for(int i=0;i<v[t1].size();i++){ 55 int t2=v[t1][i]; 56 if(color[t2]==-1){ 57 if(color[t1]==0){ 58 color[t2]=1; 59 } 60 else{ 61 color[t2]=0; 62 } 63 q.push(t2); 64 } 65 else{ 66 if(color[t1]==color[t2]){ 67 return true; 68 } 69 } 70 71 } 72 } 73 return false; 74 } 75 int main() 76 { 77 int t; 78 int ac=0; 79 scanf("%d",&t); 80 while(t--){ 81 scanf("%d%d%d",&n,&m,&s); 82 for(int i=0;i<=n;i++){ 83 v[i].clear(); 84 } 85 init(); 86 int num=n-1; 87 for(int i=0;i<m;i++){ 88 int x,y; 89 scanf("%d%d",&x,&y); 90 if(merge(x,y)){ 91 num--; 92 } 93 v[x].push_back(y); 94 v[y].push_back(x); 95 } 96 memset(color,-1,sizeof(color)); 97 printf("Case %d: ",++ac); 98 if(num!=0){ 99 printf("NO "); 100 continue; 101 } 102 103 104 if(bfs()){ 105 printf("YES "); 106 } 107 else{ 108 printf("NO "); 109 } 110 111 112 } 113 return 0; 114 }
dfs实现染色:

1 #pragma comment(linker, "/STACK:1024000000,1024000000") 2 #include<iostream> 3 #include<cstdio> 4 #include<cstring> 5 #include<cmath> 6 #include<math.h> 7 #include<algorithm> 8 #include<queue> 9 #include<set> 10 #include<bitset> 11 #include<map> 12 #include<vector> 13 #include<stdlib.h> 14 #include <stack> 15 using namespace std; 16 #define PI acos(-1.0) 17 #define max(a,b) (a) > (b) ? (a) : (b) 18 #define min(a,b) (a) < (b) ? (a) : (b) 19 #define ll long long 20 #define eps 1e-10 21 #define MOD 1000000007 22 #define N 100006 23 #define inf 1e12 24 25 //////////////////////////////////////////////////// 26 int fa[N]; 27 void init(){ 28 for(int i=0;i<N;i++){ 29 fa[i]=i; 30 } 31 } 32 int find(int x){ 33 return fa[x]==x?x:fa[x]=find(fa[x]); 34 } 35 bool merge(int x,int y){ 36 int root1=find(x); 37 int root2=find(y); 38 if(root1==root2) return false; 39 fa[root1]=root2; 40 return true; 41 } 42 /////////////////////////////////////////////////// 43 44 int n,m,s; 45 vector<int> v[N]; 46 int color[N]; 47 bool dfs(int x,int c){ 48 color[x]=c; 49 for(int i=0;i<v[x].size();i++){ 50 int y=v[x][i]; 51 if(color[y]==-1){ 52 color[y]=!c; 53 dfs(y,!c); 54 } 55 else{ 56 if(color[y]==color[x]){ 57 return true; 58 } 59 } 60 } 61 return false; 62 } 63 int main() 64 { 65 int ac=0; 66 int t; 67 scanf("%d",&t); 68 while(t--){ 69 for(int i=0;i<N;i++){ 70 v[i].clear(); 71 } 72 init(); 73 scanf("%d%d%d",&n,&m,&s); 74 int num=n-1; 75 for(int i=0;i<m;i++){ 76 int x,y; 77 scanf("%d%d",&x,&y); 78 if(merge(x,y)){ 79 num--; 80 } 81 v[x].push_back(y); 82 v[y].push_back(x); 83 } 84 85 printf("Case %d: ",++ac); 86 if(num!=0){ 87 printf("NO "); 88 continue; 89 } 90 91 memset(color,-1,sizeof(color)); 92 if(dfs(s,0)){ 93 printf("YES "); 94 } 95 else{ 96 printf("NO "); 97 } 98 99 } 100 return 0; 101 }
