我也不知道为什么我不会的大多是基础算法…
定义
对于一维来说,前缀和与差分的处理较为简单。
前缀和,即是某一数列中,第i号元素及其之前的全部元素之和。对于某数列A,其前缀和S的信息

差分。即第i项与i-1项之差。给定一个数列A,它的差分数列B为

由此可以看出,前缀和和差分是一对互逆运算。
差分序列B的前缀和序列就是原序列A
前缀和序列S的差分序列就是原序列A
上面的性质非常之重要,稍后会在二维中用到。
应用
前缀和可以快速的帮助我们求得某一个区间的和。
即对于原序列A中的一个区间(l,r),有前缀和序列S

差分可以快速的帮助我们进行区间同时加、减操作。
对于原序列A的区间(l,r)加d 其差分序列就变化为
Bl+d ,Br+1-d
其他位置均不需要改变。如果需要实装到原序列上,只需要将差分序列做一个前缀和即可。
二维
这里引用一个例题来讲解会显得比较自然
激光炸弹 BZOJ1218(前缀和)
我们以S[i,j]代表二维前缀和。那么我们接下来观察一下
S[i,j],S[i-1,j],S[i,j-1],S[i-1,j-1]

这样我们就可以得到这样的递推式
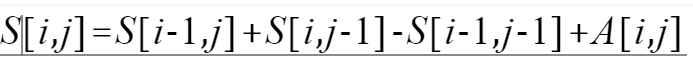
这是对于长度为1的小正方形的。我们可以由此推广到长度为R的正方形,并将公式进行移项,就可以得到以下公式
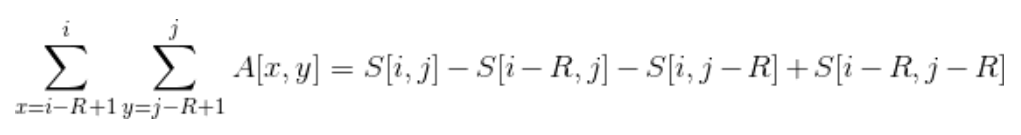
这样我们便解决了二维前缀和的问题。
有了这个方法,我们就可以枚举边长为R的正方形的右下角坐标(i,j),就可以通过公式计算出所有目标价值之和,取最大值即可。
听说这道题的空间卡的很恶心,这里我们不做讨论(因为这里不是题解)
现代艺术 NKOJ(差分)
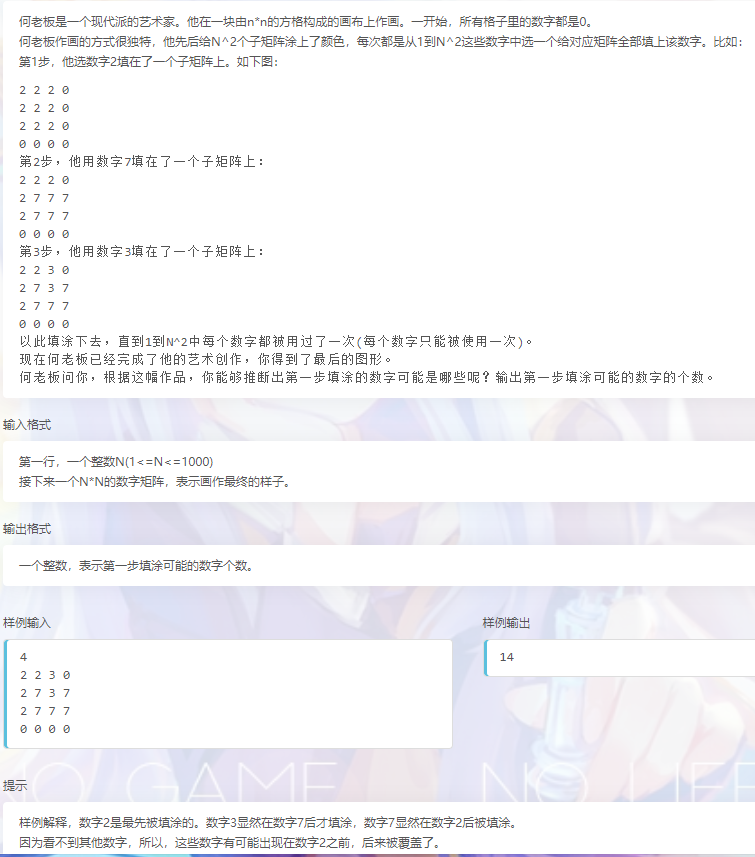
这题是南开培训的时候的一道考试题,不知道是不是自己出的,这里就不追究题目来源了。
对于这道题,我们只需要找出覆盖部分的数字。比较容易想出,如果两个数字矩阵相互覆盖,那么重复部分(被覆盖部分)上显示的数字就一定不可能是第一个数字。也就是说,我们需要求出所有矩阵交叉位置的数字,并将其排除。如果1——N2中某数字从未出现,那么他就有可能是第一位数字(被覆盖了)。但是这里需要一个特殊判断,当场上只有一个数字(除去0),那么答案就固定为N2-1,因为其他数字都已经被覆盖了。
刚开始接触这道题的时候我认为是个扫描线问题,但我没打出它的写法,这里不做讨论。
对于每一个数字,我们需要得到它的四个顶点,以来确定这个数字矩阵。
那么对于每一个数字矩阵,我们将其覆盖的范围+1。再次扫描时,如果某个点上的统计数字>1,那么就代表其又覆盖成份,其不可能成为第一个填入的数字。
如果我们暴力枚举来进行矩阵区间加法操作,那么一定会超时。根据差分的性质,我们完全可以用差分来进行区间操作,最后通过差分系列的前缀和来还原原序列。
以下是这道题的代码(因为何老板加强了数据,我没仔细听他要求用的算法是什么,所以这道题我保持了差分做法,得分80分,扣分原因是MLE)
#include<iostream> #include<cstdio> #include<vector> using namespace std; const int MAXN=1011; const int MAXNN=1000010; int n; vector<int>A; int nn; inline int read(){ int s=0,w=1; char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();} while(ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar(); return s*w; } struct Cube{ int x1; int x2; int y1; int y2; }Cubes[MAXNN]; int Map[MAXN][MAXN]; int S[MAXN][MAXN];//差分序列 bool Appear[MAXNN]; bool Used[MAXNN]; int Appears; int Orig[MAXN][MAXN];//原序列。原序列=差分序列的前缀和序列 int ans; int main(){ n=read(); nn=n*n; int Max=n+10; for(int i=1;i<=nn;i++){ Cubes[i].x1=Max; Cubes[i].y1=Max; } for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ Map[i][j]=read(); if(!Map[i][j]){ continue; } if(!Appear[Map[i][j]]){ Appear[Map[i][j]]=true; A.push_back(Map[i][j]); Appears++; } Cubes[Map[i][j]].x1=min(i,Cubes[Map[i][j]].x1); Cubes[Map[i][j]].x2=max(i,Cubes[Map[i][j]].x2); Cubes[Map[i][j]].y1=min(j,Cubes[Map[i][j]].y1); Cubes[Map[i][j]].y2=max(j,Cubes[Map[i][j]].y2); } } if(Appears==1){ printf("%d",nn-1); return 0; } for(int j=0;j<A.size();j++){ int i=A[j]; S[Cubes[i].x1][Cubes[i].y1]++; S[Cubes[i].x2+1][Cubes[i].y1]--; S[Cubes[i].x1][Cubes[i].y2+1]--; S[Cubes[i].x2+1][Cubes[i].y2+1]++; } for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ Orig[i][j]=S[i][j]+Orig[i-1][j]+Orig[i][j-1]-Orig[i-1][j-1]; if(!Used[Map[i][j]]&&Orig[i][j]>1){ Used[Map[i][j]]=true; nn--; } } } printf("%d",nn); }
我们从代码中提取到二维差分的公式:
对于区间修改操作,只需要将其左下角+k,右下角(x2+1,y1)-k。左上角-k,右上角+k
再通过二维前缀和公式,将差分序列做前缀和,得到原序列。