本篇为本人的第一篇随笔,为的是分享总结学习经验
在日后温故而知新,以便取得些许的进步,也是对学习的总结
一、主要思想
桶排序的大体思路就是先将数组分到有限个桶中,再对每个桶中的数据进行排序,可以说是鸽巢排序的一种归纳结果(对每个桶中数据的排序可以是桶排序的递归,或其他算法,在桶中数据较少的时候用插入排序最为理想)。
二、算法效率
对N个数据进行桶排序的时间复杂度分为两部分:
1、对每一个数据进行映射函数的计算(映射函数确定了数据将被分到哪个桶),时间复杂度为O(N)。
2、对桶内数据的排序,时间复杂度为∑ O(Ni*logNi) ,其中Ni 为第i个桶的数据量。
对于N个待排数据,M个桶,平均每个桶[N/M]个数据的桶排序平均时间复杂度为:O(N)+O(M*(N/M)*log(N/M))=O(N+N*(logN-logM))=O(N+N*logN-N*logM),当N=M时,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
对于相同数量的数据,桶的数量越多,数据分散得越平均,桶排序的效率越高,可以说,桶排序的效率是空间的牺牲换来的。
三、算法分析
1、初始化桶
桶排序中的桶其实是一组指向指针的指针,有点类似于哈希表中的链地址法,与之不同的是桶本身也是结构体(图1是链地址法,图2为初始化后的桶)
 (图一)
(图一)
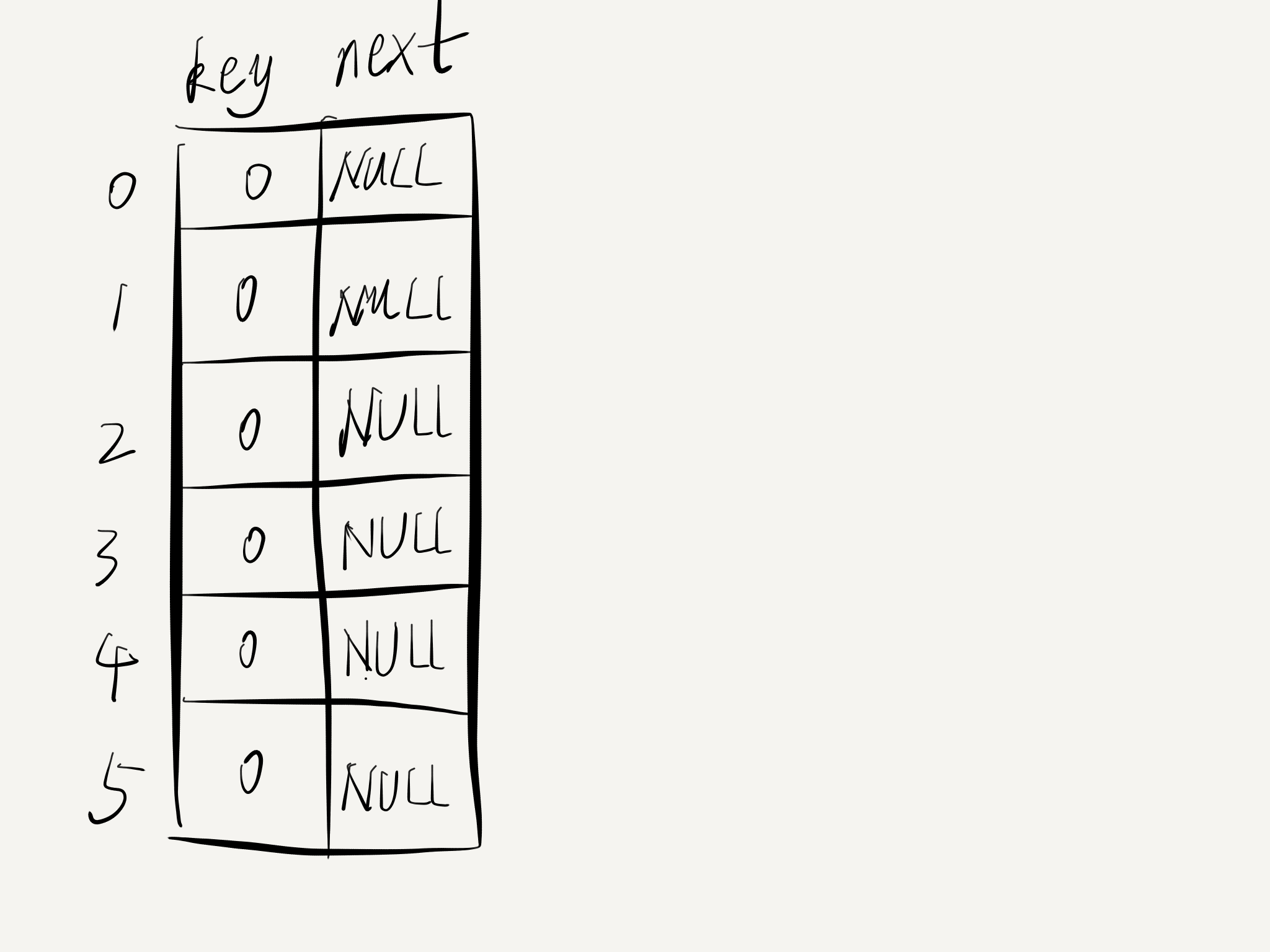 (图二)
(图二)
2、将数据放入相应的桶的同时对该桶排序
遍历数据,根据映射函数对数据进行计算,下图的映射函数为N/10(N是当前数据),确定了桶之后,将数据在桶中采用直接插入法。下图为对数组a的桶排序。
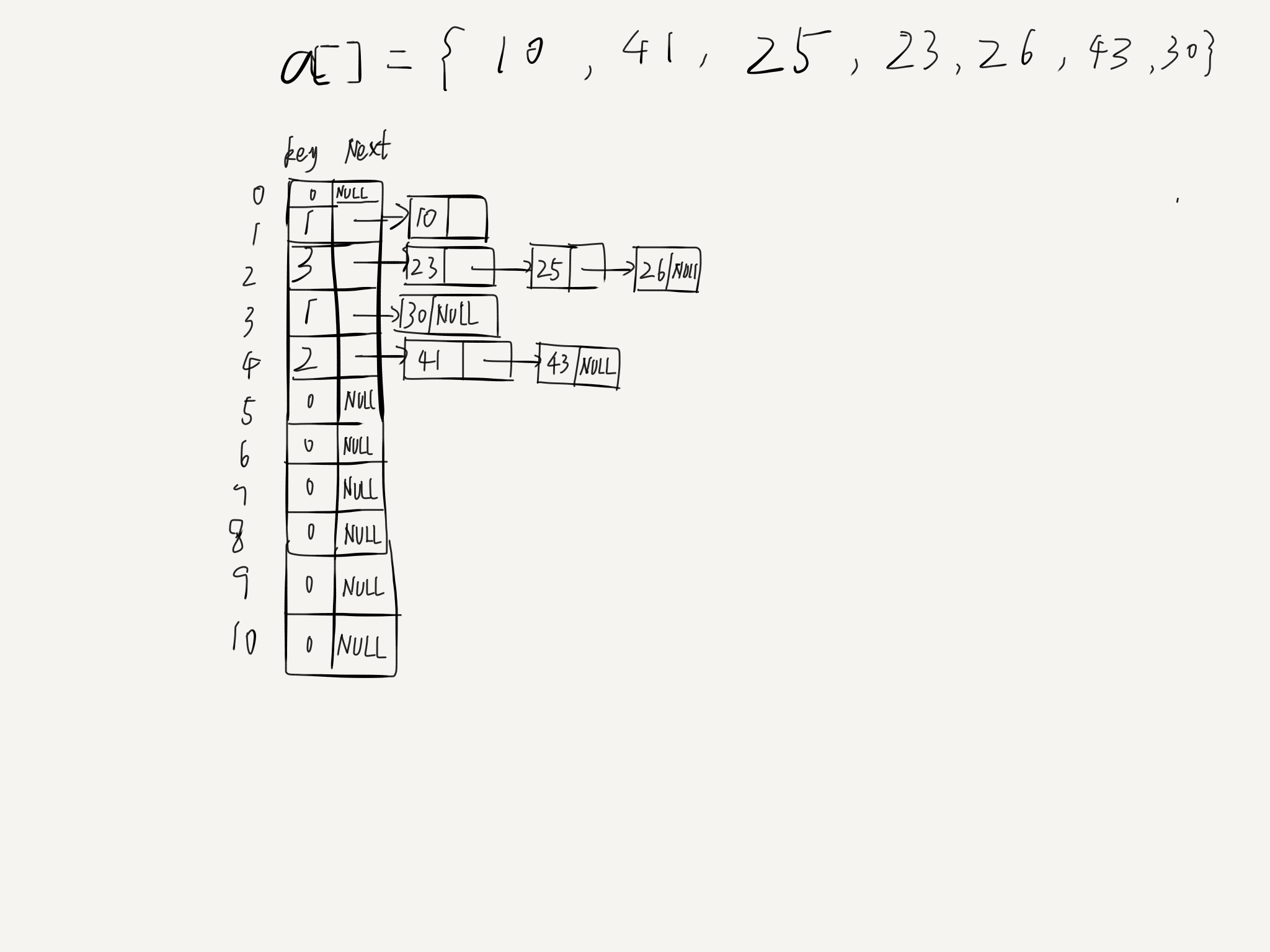
(图中key是桶中数据个数)
以25和23为例,25/10=2,确定25的位置在第二个桶,此时桶2还没有元素,所以直接插入,23/10=2,确定在第二个桶,此时桶2的key不为0,23<25将23插入25之前,其他的类似。
3、按按照桶的顺序将元素输出
按上图中的情况,排序后的顺序就为:10 23 25 26 30 41 43
四、复杂度及应用分析
桶排序的平均时间复杂度为线性的O(N+C),其中C=N*(logN-logM)。如果相对于同样的N,桶数量M越大,其效率越高,最好的时间复杂度达到O(N)。当然桶排序的空间复杂度为O(N+M)。
在很多情况下N=M,即极限情况下每个桶只有一个数据时。桶排序的最好效率能够达到O(N)。
五、代码展示(C语言)
#include<stdlib.h>
typedef struct node{
int key;
struct node* next;
}KeyNode;
void bucket_sort(int keys[],int size,int bucket_size);
int main()
{
int a[]={11,11,9,21,14,55,77,99,53,25};
int size=sizeof(a)/sizeof(a[0]);
bucket_sort(a,size,10);
return 0;
}
void bucket_sort(int keys[],int size,int bucket_size)
{
KeyNode **bucket_table=(KeyNode**)malloc(bucket_size*sizeof(KeyNode*));
for(int i=0;i<bucket_size;i++){ //初始化桶
bucket_table[i]=(KeyNode*)malloc(sizeof(KeyNode));
bucket_table[i]->key=0;
bucket_table[i]->next=NULL;
}
for(int i=0;i<size;i++){
KeyNode* node=(KeyNode*)malloc(sizeof(KeyNode));
node->key=keys[i];
node->next=NULL;
int index=keys[i]/10;//给数据分类的方法(关系到排序速度,很重要)
KeyNode *p=bucket_table[index];
if(p->key==0){
p->next=node;
p->key++;
}
else{
while(p->next!=NULL&&p->next->key<=node->key){//=的时候后来的元素会排在后面
p=p->next;
}
node->next=p->next;
p->next=node;
(bucket_table[index]->key)++;
}
}
KeyNode* k=NULL;
for(int i=0;i<bucket_size;i++){
for(k=bucket_table[i]->next;k!=NULL;k=k->next){
printf("%d ",k->key);
}
}
}