最长递增子序列问题图文分析

一、题目：

求一个由n个整数组成的整数序列的最长递增子序列。一个整数序列的递增子序列可以是序列中非连续的数按照原序列顺序排列而成的。 最长递增子序列是其递增子序列中长度最长的。

二、解题思路：

创建一个结果字符串，用于保存最长子序列。

对于原序列中的每个数，若满足条件可以选择放入或不放入，若不满足条件，则不可放入。

通过递归的思想，可以很快将序列的所有可能结果得出，再通过判断其大小，从而选出最大的序列。

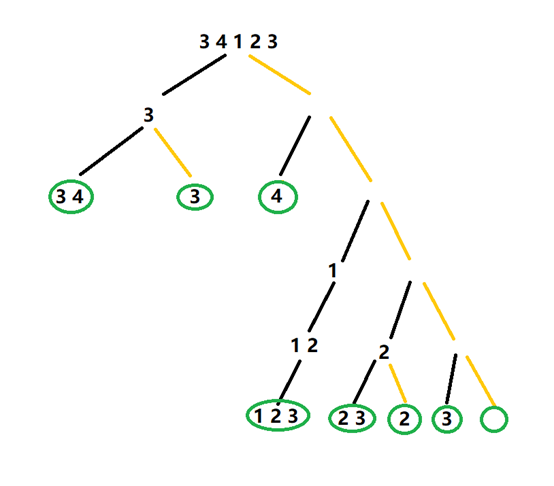
上图分析：

　　黑线代表放入符合条件的下一个数，黄线表示不放入，绿色椭圆里的序列即为最后可能得到的结果（上图得到123的支线还没画完整）。

　　以34123为例，一开始可以选择往答案序列放入3或不放入3，放入3后可以选择放入4或不放入4（放入的数必须大于前一个放入的数），一直这样下去，直到读到原始序列的最后一个数或再也找不出符合条件的数，最后通过比较，得到答案序列最长的序列。

三、实现代码

public class Long_list {
    public String list(char s[]) {
        String t = "";
        return l(s, t, 0);
    }

    private String l(char s[], String t, int lo) {// 从头到尾判断符合条件的每一位放入与不放入的情况
        if (lo > s.length - 1) {// 最后一位已经判断完 出口1
            return t;
        }
        String k = "";
        for (int i = lo; i < s.length; i++) {
            if ((t.length() == 0) || ((t.length() - 1 >= 0) && t.charAt(t.length() - 1) < s[i])) {
                k = t + s[i];// 连接
                break;
            }
        }
        return max(l(s, t, lo + 1), l(s, k, lo + 1));
    }

    private String max(String l, String l2) {
        return l.length() >= l2.length() ? l : l2;
    }

    public static void main(String[] args) {
        char c[] = { '3', '1', '4', '2', '3' };
        Long_list ll = new Long_list();
        System.out.println(ll.list(c));
    }
}