hdu6073[dfs+删边] 2017多校4

题目中对二分图的定义十分特殊， 指的是 U，V两部分中，U的顶点度数必定为2，V中顶点无限制。

题目要求的是 对于所有匹配，该匹配的权值=该匹配中选中的边的边权的乘积，求所有匹配权值之和。

对于V中的顶点，a∈V ， 如果a的度数为1， 那么a的最优匹配就已经决定了，此时将a对答案的贡献记录下来(ans乘上该边的权即可，因为任意一种匹配都必定包含此边)。

删去a点后，所有与a相连的顶点度数-1，如果这个时候又出现了度数为1的顶点，就重复类似a的操作，直到图中再无度数为1的顶点。

可以发现，这就是无向图判环的一种方法。剩下的顶点度数必定为2(题目中的特殊条件限制)，且构成x个环。

对于每个环我们可以发现

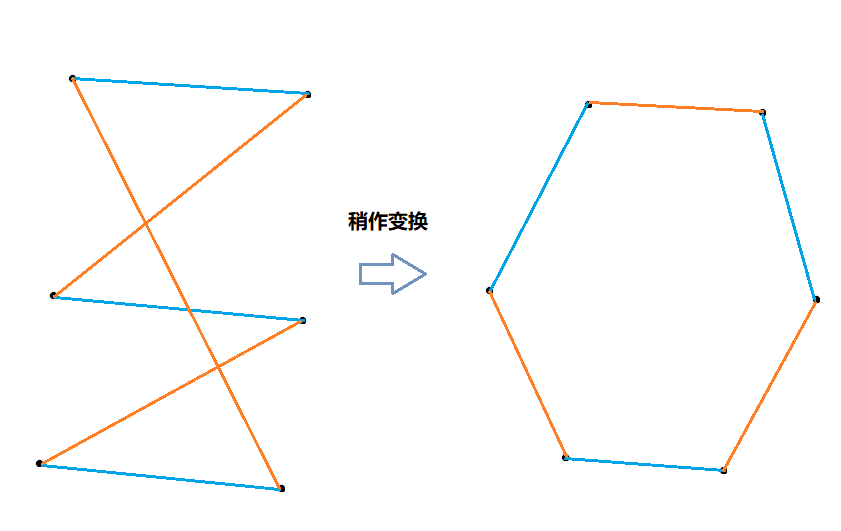
都会只有两种取法使得最优匹配，这种跳着取边算贡献的过程我们可以用dfs实现。

题目中，一种 最优匹配的权值 是 最优匹配中所有边的乘积，所以对于一个环，我们算出 Sum_蓝色=∏蓝色边  Sum_红色=∏红色边

计算(Sum_蓝色+Sum_红色)与当前的ans相乘即可，因为任意 两个环之间的最优匹配都可以随意配对 比如 环_a红色配环_b蓝色， 环_a蓝色配 环b蓝色...

/*hdu6073[dfs+删边] 2017多校4*/
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL MOD = 998244353LL;
struct Edge {
    int to, cost;
    Edge(int T = 0, int C = 0)
        : to(T), cost(C) {}
};
vector<Edge>G[600005];
int deg[600005];
bool vis[600005];
int T, n, u, v, w;
LL x = 1, y = 1;
LL res = 1, ans = 1;
void init() {
    res = 1, ans = 1;
    for (int i = 0; i <= 2 * n; i++) {
        G[i].clear();
    }
    memset(deg, 0, sizeof(deg));
    memset(vis, 0, sizeof(vis));
}
void dfs(int u, int fa, int c) {
    if (vis[u]) return;
    vis[u] = 1;
    for (int i = 0; i < (int)G[u].size(); i++) {
        Edge &e = G[u][i];
        if (e.to == fa || deg[e.to] != 2) continue;
        dfs(e.to, u, c ^ 1);
        if (c) x = (x * e.cost) % MOD;
        else y = (y * e.cost) % MOD;
        break;
    }
    return;
}
void solve() {
    queue<int>q;
    for (int i = 1; i <= 2 * n; i++) {
        if (deg[i] == 1) {
            q.push(i);
        }
    }
    while (!q.empty()) {
        int u = q.front();
        q.pop();
        deg[u]--;
        for (int i = 0; i < (int)G[u].size(); i++) {
            Edge &e = G[u][i];
            deg[e.to]--;
            if (!vis[e.to] && !vis[u]) {
                vis[e.to] = vis[u] =  1;
                res = (res * e.cost) % MOD;
            }
            if (deg[e.to] == 1) {
                q.push(e.to);
            }
        }
    }
    memset(vis, 0, sizeof(vis));
    for (int i = 1; i <= 2 * n; i++) {
        if (deg[i] == 2 && !vis[i]) {
            x = 1, y = 1;
            dfs(i, i, 1);
            //cout << x << ' ' << y << endl;
            ans = (ans * (x + y)) % MOD;
        }
    }
    ans = (ans * res) % MOD;
    printf("%lld
", ans);
}
int main() {
    //freopen("1007.in", "r", stdin);
    //freopen("1007.txt", "w", stdout);
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        init();
        for (int i = 1; i <= n; i++) {
            scanf("%d%d", &v, &w);
            G[i].push_back(Edge(v + n, w));
            G[v + n].push_back(Edge(i, w));
            deg[i]++, deg[v + n]++;
            scanf("%d%d", &v, &w);
            G[i].push_back(Edge(v + n, w));
            G[v + n].push_back(Edge(i, w));
            deg[i]++, deg[v + n]++;
        }
        solve();
    }
    return 0;
}