dd爱科学1.0（牛客）

题面：

链接：https://ac.nowcoder.com/acm/contest/11211/A
来源：牛客网

大科学家dddddd最近在研究转基因白菜，白菜的基因序列由一串大写英文字母构成，dddddd经过严谨的推理证明发现，只有当白菜的基因序列呈按位非递减形式时，

这株白菜的高附加值将达到最高，于是优秀的dddddd开始着手修改白菜的基因序列，dddddd每次修改基因序列的任意位需要的代价是111，dddddd想知道，

修改白菜的基因序列使其高附加值达到最高，所需要的最小代价的是多少。

题解：

 类似于最长公共子序列的变形？

我们设最长公共子序列为lsc（x,y）,看看最长公共子序列的状态转移方程:

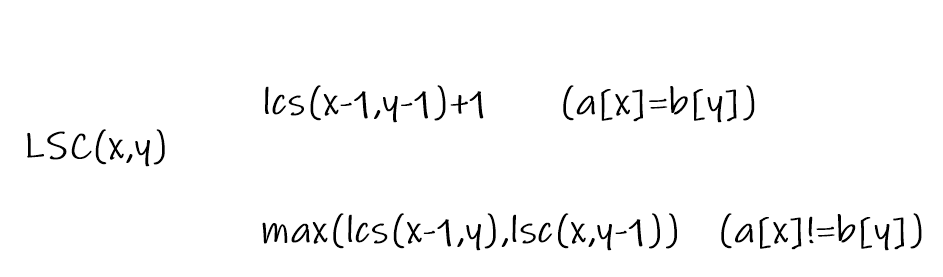
我们再分析这道题，输入的字符串如果要更改的少，那就要按‘A’到‘Z’顺序可重复的公共子序列最长。

设满足条件的子序列为f(x,y),

当a[n]!=b[m]时，我们会产生两个子问题：

•   f(x-1,y)     //在a[1]~a[x-1]区间和b[1]~b[y]继续寻找最优解
•   f(x,y-1)     //在a[1]~a[x]区间和b[1]~b[y-1]继续寻找最优解

因为a[n]!=b[m],两个字符串的最后一个字符中肯定有一个不是f(x,y)，解决以上两个子问题，找到最优解。 

当a[i]=b[i]时，我们也会遇到这两种情况：

• f(x,y-1)  
• f(x-1,y)

不同的是，长度都能+1，因为a[n]=b[m],可以选择两种情况的最大值进行比较。

最后我们得出状态方程：

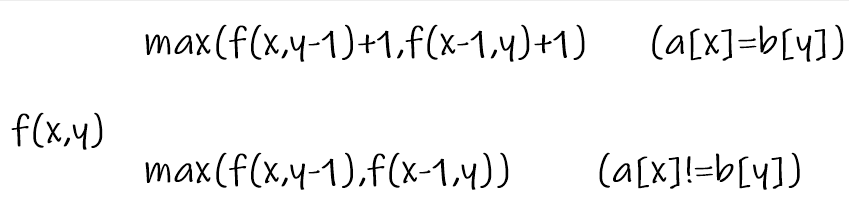
就是这样了，o((>ω< ))o！

ACcode：

char a[1000100],p;
ll n,dp[1000100][28];
int main() {
    scanf("%lld", &n);
        scanf("%s", a + 1);
        int flag = a[0], num = 1;
        memset(dp, 0, sizeof dp);
        for (int i = 1; i <= n; i++) {
            for (int j = 0; j < 26; j++) {
                p = j + 'A';
                if(p!=a[i])
                dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
                else if (p == a[i])
                dp[i][j] = max(dp[i][j-1]+1, dp[i - 1][j] + 1);
            }
        }
        cout << n - dp[n][25];//减去f(n,25)就可以得到需要改变的最小值了。
    return 0;
}