快速幂

快速幂的目的是做到快速求幂，假设我们要求a^b,按照朴素算法就是把a连乘b次，这样一来时间复杂度是O(b)也即是O(n)级别，快速幂能做到O(logn)，快了很多。

当b=11时，b的二进制：1011，。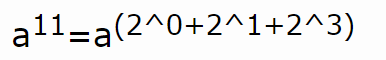

  

&运算通常用于二进制取位操作，例如一个数 & 1 的结果就是取二进制的最末位。还可以判断奇偶x&1==0为偶，x&1==1为奇。

幂运算是非常常见的一种运算，求取a^n,最容易想到的方法便是通过循环逐个累乘，其复杂度为O(n)，这在很多时候是不够的，所以我们需要一种算法来优化幂运算的过程。

一、快速幂——反复平方法

该怎样去加速幂运算的过程呢？既然我们觉得将幂运算分为n步进行太慢，那我们就要想办法减少步骤，把其中的某一部分合成一步来进行。

比如，如果n能被2整除，那我们可以先计算一半，得到a^(n/2)的值，再把这个值平方得出结果。这样做虽然有优化，但优化的程度很小，仍是线性的复杂度。

再比如，如果我们能找到2^k == n，那我们就能把原来的运算优化成((((a^2)^2)^2)...)，只需要k次运算就可以完成，效率大大提升。可惜的是，这种条件显然太苛刻了，适用范围很小。不过这给了我们一种思路，虽然我们很难找到2^k == n，但我们能够找到2^k1 + 2^k2 + 2^k3 +......+ 2^km == n。这样，我们可以通过层层递推，在很短的时间内求出各个项的值。可是又有新的问题出现了，我们并不清楚k1、k2...km具体的值是多少，对于不同的n，有不同分法，有没有一种规则能把这些分法统一起来。

我们都学习过进制与进制的转换，知道一个b进制数的值可以表示为各个数位的值与权值之积的总和。比如，2进制数1001，它的值可以表示为10进制的1*2^3 + 0*2^2 + 0*2^1 + 1*2^0，即9。这完美地符合了上面的要求。可以通过2进制来把n转化成2^km的序列之和，而2进制中第i位（从右边开始计数，值为1或是0）则标记了对应的2^(i - 1)是否存在于序列之中。譬如，13为二进制的1101，他可以表示为2^3 + 2^2 + 2^0，其中由于第二位为0，2^1项被舍去。

如此一来，我们只需要计算a、a^2、a^4、a^8......a^(2^km)的值（这个序列中的项不一定都存在）并把它们乘起来即可完成整个幂运算。借助位运算的操作，可以很方便地实现这一算法，其复杂度为O(logn)。

typedef long long ll;
ll quick_pow(ll a, ll n)//a^n
{
    ll re = 1;
    while(n != 0)
    {
        if(n & 1)//判断n的最后一位是1还是0
            re *= a;
        a = (a * a);//将a平方，即把a^(2^i)变为a^(2^(i + 1))
        n >>= 1;//n右移一位，舍去n的最后一位
    }
    return re;
}