AOV网
在日常生活中,一项大的工程可以看作是由若干个子工程(这些子工程称为“活动” )组成的集合,这些子工程(活动)之间必定存在一些先后关系,即某些子工程(活动)必须在其它一些子工程(活动)完成之后才能开始,我们可以用有向图来形象地表示这些子工程(活动)之间的先后关系,子工程(活动)为顶点,子工程(活动)之间的先后关系为有向边,这种有向图称为“顶点活动网络” ,又称“AOV网” 。
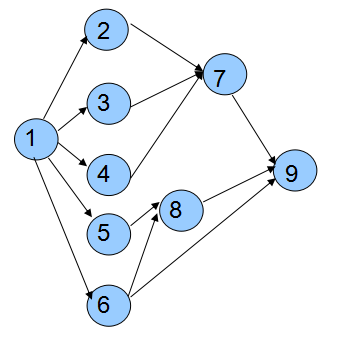
在AOV网中,有向边代表子工程(活动)的先后关系,我们把一条有向边起点的活动成为终点活动的前驱活动,
同理终点的活动称为起点活动的后继活动。而只有当一个活动全部的前驱全部都完成之后,这个活动才能进行。
例如在上图中,只有当工程1完成之后,工程2、3、4、5、6才能开始进行。只有当2、3、4全部完成之后,7才能开始进行。
一个AOV网必定是一个有向无环图,即不应该带有回路。否则,会出现先后关系的自相矛盾。
拓扑排序算法
只适用于AOV网(有向无环图)。
把AOV网中的所有活动排成一个序列, 使得每个活动的所有前驱活动都排在该活动的前面,这个过程称为“拓扑排序”
所得到的活动序列称为“拓扑序列”。 一个AOV网的拓扑序列是不唯一的
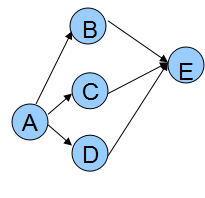
例如下面的这张图,它的拓扑序列可以是:
ABCDE,也可以是ACBDE,或是ADBCE。
在下图所示的AOV网中,工程B和工程C显然可以同时进行,先后无所谓;但工程E却要等工程B、C、D都完成以后才能进行。
例题:
洛谷P2814
代码:
#include<cstdio> #include<iostream> #include<map> using namespace std; map<string,string>p; string f(string x) { if(x!=p[x]) p[x]=f(p[x]); return p[x]; } string s,s1; int main() { char ch; cin>>ch; while(ch!='$') { cin>>s; if(ch=='#') { s1=s; if(p[s]=="") p[s]=s; } else if(ch=='+') p[s]=s1; else cout<<s<<' '<<f(s)<<endl; cin>>ch; } return 0; }