曾经搞过几天的生成函数,也没做几道题,后来放弃了,今天讲了生成函数和背包问题的结合,趁着脑子清醒整理一下;
题目描述:
明明这次又要出去旅游了,和上次不同的是,他这次要去宇宙探险!
我们暂且不讨论他有多么NC,他又幻想了他应该带一些什么东西。理所当然的,你当然要帮他计算携带N件物品的方案数。
他这次又准备带一些受欢迎的食物,如:蜜桃多啦,鸡块啦,承德汉堡等等
当然,他又有一些稀奇古怪的限制:
每种食物的限制如下:
承德汉堡:偶数个
可乐:0个或1个
鸡腿:0个,1个或2个
蜜桃多:奇数个
鸡块:4的倍数个
包子:0个,1个,2个或3个
土豆片炒肉:不超过一个。
面包:3的倍数个
注意,这里我们懒得考虑明明对于带的食物该怎么搭配着吃,也认为每种食物都是以‘个’为单位(反正是幻想嘛),只要总数加起来是N就算一种方案。因此,对于给出的N,你需要计算出方案数,并对10007取模。
输入样例1
1
输出样例1
1
输入样例2
5
输出样例2
35
数据范围
对于40%的数据,1<=N<=100000;
对于所有数据,1<=n<=10^500;
对于小数据范围的,我们显然可以用dp的背包问题处理,那么对于本题这么大的范围,我们该怎么处理呢,这就要用生成函数搞一下了;
我们讲每一个要求编号;
对于1.偶数个:生成函数是1+$x^2$+$x^4$+$x^6$+$x^8$+...=$frac{1}{1-$x^2$}$
对于2:1+x;
对于3:1+x+$x^2$=$frac{1+$x^3$}{1-x}$;
算了我搞不了博客园的公式,还是搞图片吧;
来自ppt,其实每一个式子都很好推导;

对于式子七等,我们可以采取先求多项式的逆元,再将其化简的方法会比较方便;
那么这个题目就是让我们求f(x)的第n-1项,为什么是n-1呢,因为分子上的x相当于一个位移的作用;
那么我们探讨一下(1-x)-4的第[n]项系数怎么求;有两种思路;
第一种:广义二项式定理;
对于负数的情况,如下;
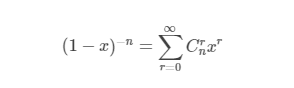
那么答案十分显然,我们将其展开,就是C(3,n+2)
第二种思路:对于这个母函数的第n项的系数,相当于不定方程x1+x2+x3+...+xn=4的非负整数解的个数,
这个问题可以用组合数学中的插板法解决,答案也为C(3,n+2);
注意:这里的n是已经减过1的n;