街道赛跑

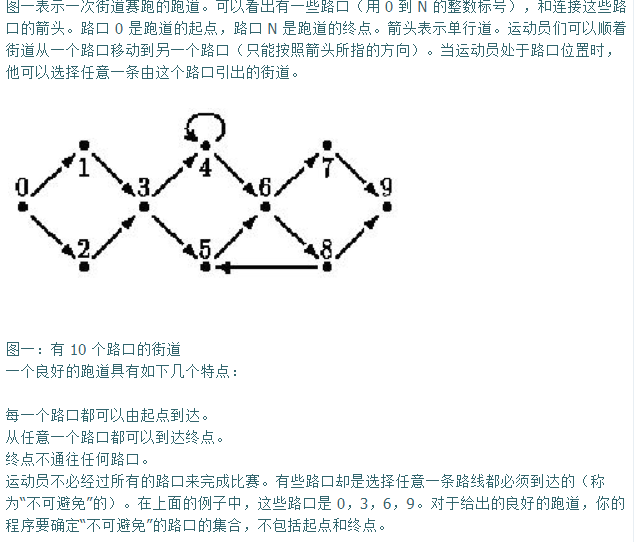
首先第一问不难做到，我们可以去掉当前这个点，然后进行bfs，如果去掉之后当前这个点从起点不能到达终点，那个这个点就是必经路口；

那么针对第二问，我们首先能看出来是不可避免的路口（称为s集合），那么s集合中的点一定是第一问中的必经路口，很显然叭；

那么我们可以两步找到这个点，首先从起点开始bfs，标记所能到达的所有点，然后从当前枚举的必经路口中的点开始bfs，并且标记；

最后我们寻找0-n中的点s如果既没有被起点标记，又没有被当前点标记，那么当前枚举的这个点就是s集合中的点；

提供工整的代码

#include<bits/stdc++.h>
using namespace std;
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)) {if(ch=='-') f=-1;ch=getchar();}
    while(isdigit(ch)) {x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}
    return x*f;
}
int h[5100],g[5100][5100],vis1[5100],n,vis2[5100],ans1[5100],ans2[5100],x,head,tail,tot,sum;
int main()
{
    x=read();
    while(x!=-1)
    {
        while(x!=-1&&x!=-2)
        {
            g[n][x]=1;
            x=read();
        }
        n++;
        x=read();
    }
    n--;
    for(int i=1;i<=n-1;i++)
    {
        memset(vis1,0,sizeof(vis1));
        head=1;tail=1;
        h[head]=0;
        vis1[i]=1,vis1[0]=1;
        while(head<=tail)
        {
            int k=h[head];
            head++;
            for(int z=1;z<=n;z++)
            {
                if(g[k][z]&&vis1[z]==0) 
                {
                    h[++tail]=z;
                    vis1[z]=1;
                }
            }
        }
        if(!vis1[n])
        {
            tot++;
            ans1[tot]=i;
        }
    }
    cout<<tot<<' ';
    for(int i=1;i<=tot;i++) cout<<ans1[i]<<' ';
    cout<<endl;    
    for(int i=1;i<=tot;i++)
    {
        memset(vis1,0,sizeof(vis1));
        memset(vis2,0,sizeof(vis2));
        vis1[ans1[i]]=1;vis1[0]=1;
        vis2[ans1[i]]=1;
        head=1;tail=1;
        h[head]=0;
        while(head<=tail)
        {
            int m=h[head];
            head++;
            for(int z=0;z<=n;z++)
            {
                if(g[m][z]&&!vis1[z])
                {
                    vis1[z]=1;
                    h[++tail]=z;
                }
            }
        }
        head=1;tail=1;
        h[head]=ans1[i];
        while(head<=tail)
        {
            int k=h[head];
            head++;
            for(int z=0;z<=n;z++)
            {
                if(g[k][z]&&!vis2[z])
                {
                    h[++tail]=z;
                    vis2[z]=1;
                }
            }
        }
        int b=1;
        for(int s=0;s<=n;s++)
        {
            if(s!=ans1[i]&&vis1[s]&&vis2[s])
            {
                b=0;
                break;
            }
        }
        if(b)    ans2[++sum]=ans1[i];
    }
    cout<<sum<<' ';
    for(int i=1;i<=sum;i++)
    cout<<ans2[i]<<' ';
    return 0;
}