LeetCode刷题记录（三）

剑指 Offer 30. 包含min函数的栈

利用辅助桟s2来存放最小值，如果有比s2更小的则让更小的进s2，当原s1中最小值出栈时，判断如果同s2值相当，代表需要更新最小值，则s2栈顶出栈

class MinStack {
public:
    stack<int>s1;
    stack<int>s2;
    
    /** initialize your data structure here. */
    MinStack() {
        s2.push(INT_MAX);
    }
    
    void push(int x) {
        s1.push(x);
        if(x<=s2.top()){	
            s2.push(x);
        }
    }
    void pop() {
        if(s1.top()==s2.top())  s2.pop(); //s1出栈元素同s2栈顶保存的最小值相等
        s1.pop();        
    }
    int top() {
        return s1.top();
    }   
    int min() {
        return s2.top();	//s2的栈顶始终保存最小值
    }
};

面试题32 - I. 从上到下打印二叉树

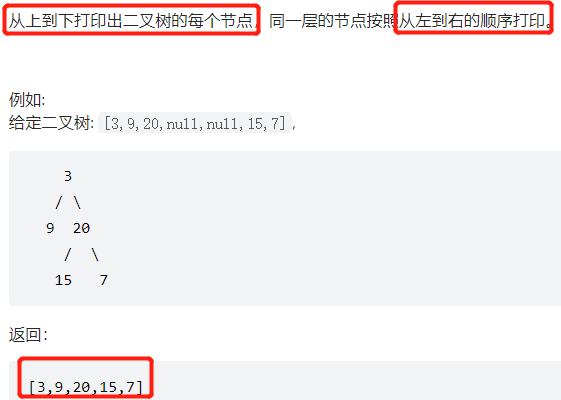
二叉树的层次遍历 3，9,20,15,7依次入队

class Solution {
public:
    vector<int> levelOrder(TreeNode* root) {
        vector<int>v;
        if(root == NULL)    return v;
        queue<TreeNode*>q;	//初始化队列
        q.push(root);	    //根结点入队
        while(!q.empty()){
            TreeNode * node = q.front();	//队首出队
            q.pop();
            v.push_back(node->val);			
            if(node->left)  q.push(node->left);		//该结点的左孩子入队
            if(node->right)  q.push(node->right);	//右孩子入队
        }
        return v;
    }
};

剑指 Offer 32 - II. 从上到下打印二叉树 II

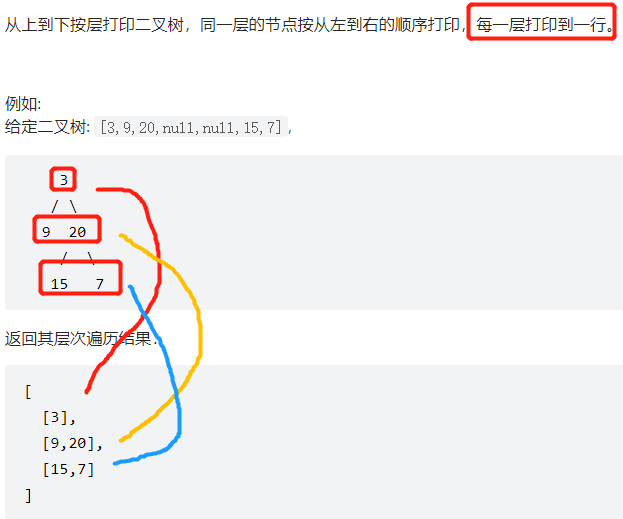
和上一题差不多一模一样，就是多了一个分层输出，怎么分层：根结点入队，队列size()为1，根结点左右孩子入队，队列size()为2，假设为满二叉树，则再向下，size()为4.......一直这样，每层有几个结点就i=q.size()，再i--把每个结点输出

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // 层次遍历问题
        vector<vector<int>> v;
        if(root==NULL){
            return v;
        }
        queue<TreeNode *>q;
        q.push(root);
        while(!q.empty()){	//队列非空时
        vector<int>temp;
            for(int i=q.size();i>0;i--)	//关键的分层的办法
            {
                TreeNode * node = q.front();
                q.pop();
                temp.push_back(node->val);
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
            v.push_back(temp);	//保存这一层的结果
        }
        return v;
    }
};

剑指 Offer 32 - III. 从上到下打印二叉树 III![image-20220306113134809]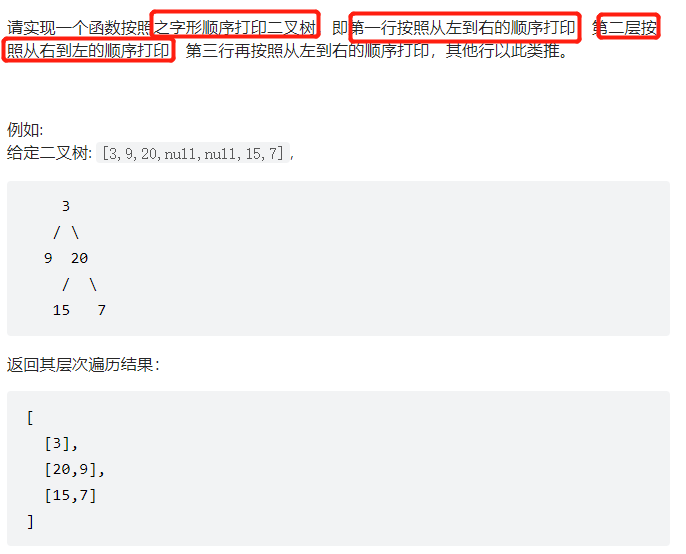

方法一：和上一题一样，但是用一个数字来记录层数，然后奇数层正常，偶数层反转一下就可以了

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        // 层次遍历问题
        vector<vector<int>> v;
        if(root==NULL){
            return v;
        }
        queue<TreeNode *>q;
        q.push(root);
        int deep = 1;
        while(!q.empty()){//队列非空时
        vector<int>temp;
        
            for(int i=q.size();i>0;i--)//关键的分层的办法
            {
                TreeNode * node = q.front();
                q.pop();
                temp.push_back(node->val);
                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }
            if(deep%2 ==0){
                reverse(temp.begin(),temp.end());
            }
            v.push_back(temp);
            deep++;
        }
        return v;
    }
};

还可以用双端队列

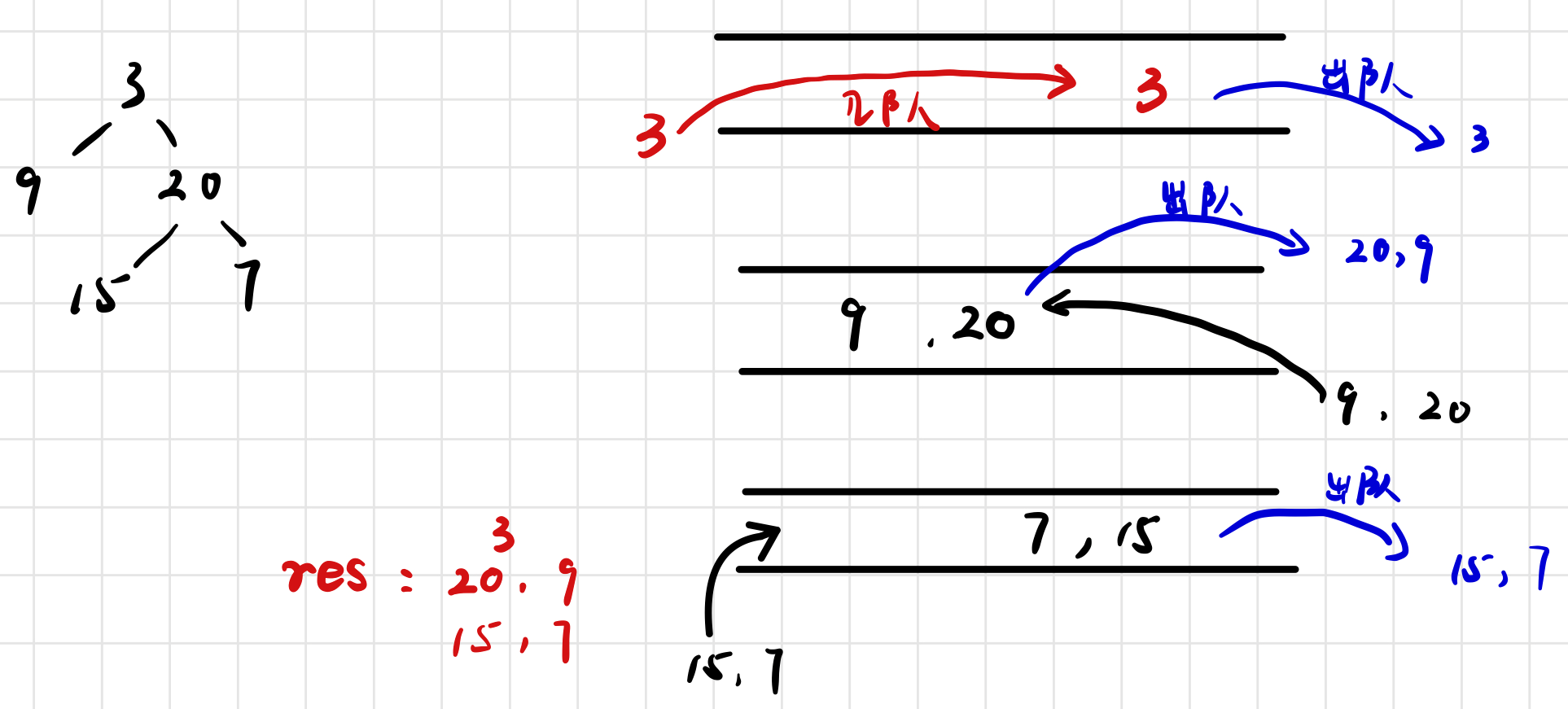
// 使用双端队列 （树的偶层: 尾入(先左子结点再右子结点)头出; 树的奇层: 头入(先右子结点再左子结点)尾出）
class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        if (root == nullptr) {
            return {};
        }

        vector<vector<int>> vec;
        deque<TreeNode*>dqe;           

        int level = 0;
        dqe.push_back(root);                   // root结点在第0层(偶层)，所以从队列尾入
        while (!dqe.empty()) {
            int level_nodes = dqe.size();
            vec.push_back({});

            if (level % 2 != 0) {              // 奇层: 从队列头入(先右子结点再左子结点)，队列尾出
                while (level_nodes) {
                    TreeNode* p_node = dqe.back();
                    if (p_node->right != nullptr) dqe.push_front(p_node->right);
                    if (p_node->left != nullptr) dqe.push_front(p_node->left);

                    vec[level].push_back(p_node->val);
                    dqe.pop_back();
                    --level_nodes;
                }
                ++level;
            }
            else {                             // 偶层: 从队列尾入(先左子结点再右子结点)，队列头出
                while (level_nodes) {
                    TreeNode* p_node = dqe.front();
                    if (p_node->left != nullptr) dqe.push_back(p_node->left);
                    if (p_node->right != nullptr) dqe.push_back(p_node->right);

                    vec[level].push_back(p_node->val);
                    dqe.pop_front();
                    --level_nodes;
                }
                ++level;
            }
        }

        return vec;
    }
};

88. 合并两个有序数组

就是说给两个非递减的数组，然后让你把第一个数组的前n位和第二个数组的前m位合并到一个数组1中（数组1的长度为M+N）

逆序双指针（双指针的思想常用）

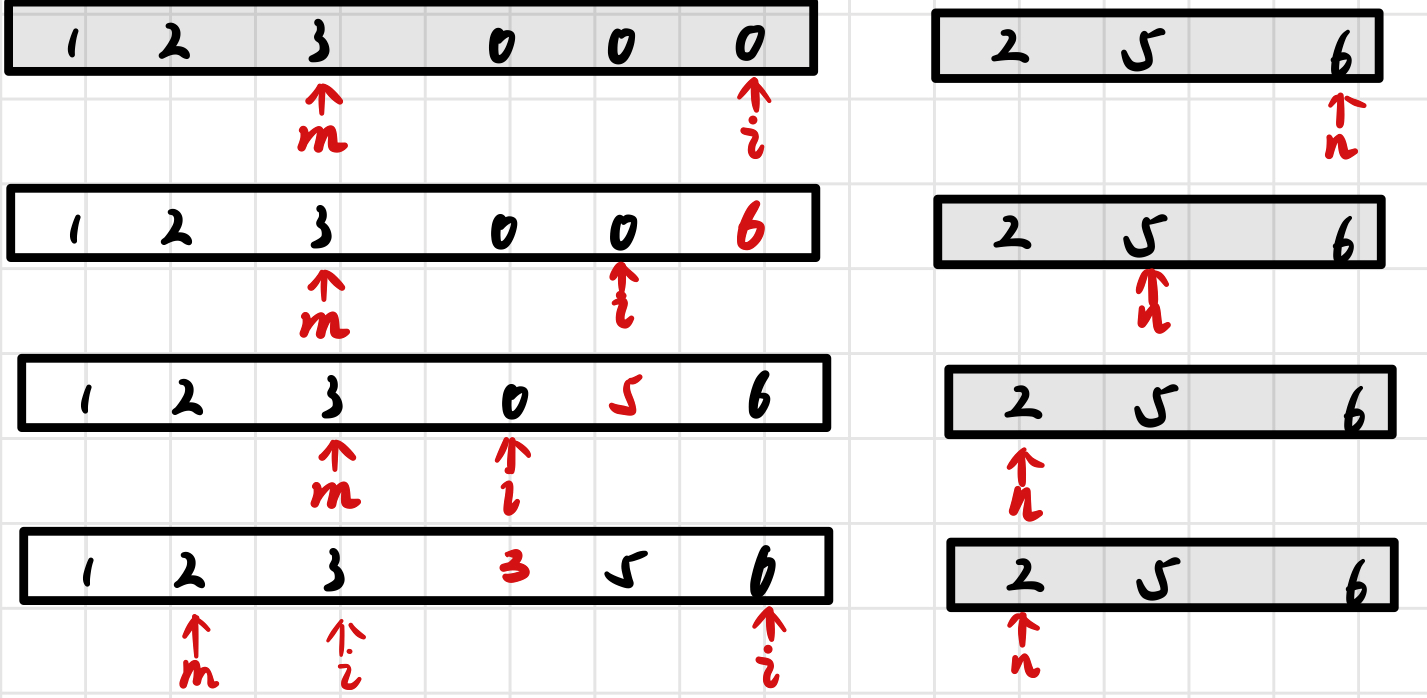
class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
    int i = nums1.size() - 1;
    m--;	 //下标从0开始，所以先减1
    n--;
    while (n >= 0) {
        while (m >= 0 && nums1[m] > nums2[n]) {
            nums1[i--]=nums1[m--];
        }
        nums1[i--]=nums2[n--];
    }
}

剑指 Offer 39. 数组中出现次数超过一半的数字

这题是408出现过的原题，最好想的是做统计，排序，但这题用的是投票法

因为一定出现众数，每次出现众数就+1，不是就-1，最后一定大于0

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int res = nums[0];	//先设nums[0]为众数
        int count = 1;
        for(int i = 1;i<nums.size();i++){
            if(nums[i]==res){	//值相等++
                count++;
            }else{	//值不等进一步判断
                if(count==1){	//仅剩1次，那么将众数更新
                    res = nums[i];
                }else{
                    count--;	//出现次数--
                }
            }
        }
        return res;
    }
};

大佬的写法：本题具有特殊性，即不用判断是否为众数，最好还是可以加上一个判断

class Solution {
public:
    int majorityElement(vector<int>& nums) {
        int x = 0, votes = 0, count = 0;
        for(int num : nums){
            if(votes == 0) x = num;
            votes += num == x ? 1 : -1;
        }
        // 验证 x 是否为众数
        for(int num : nums)
            if(num == x) count++;
        return count > nums.size() / 2 ? x : 0; // 当无众数时返回 0
    }
};

剑指 Offer 40. 最小的k个数

4种解法秒杀TopK（快排/堆/二叉搜索树/计数排序）❤️ - 最小的k个数 - 力扣（LeetCode） (leetcode-cn.com)

剑指 Offer 40. 最小的 k 个数（基于快速排序的数组划分，清晰图解） - 最小的k个数 - 力扣（LeetCode） (leetcode-cn.com)

1.快速选择算法

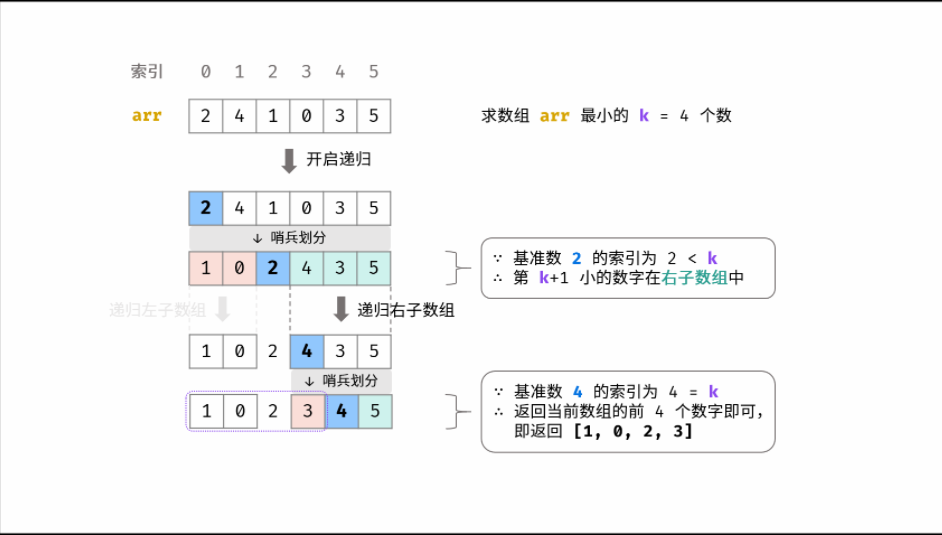
优化了的快速排序，因为只需要找出最小的k个，并不关心他们的顺序

同快排一样使用频率很高

class Solution {
public:
    vector<int> getLeastNumbers(vector<int>& arr, int k) {

        if(k>=arr.size())    return arr;
        return quick_select(arr, k, 0, arr.size() - 1);
    }
    vector<int>quick_select(vector<int>&arr,int k,int low,int high){
        int i = low;
        int j = high;
        int pivot = arr[i];//选定枢轴
        while(i<j){
            while(i<j && arr[j]>=pivot)  --j;
            arr[i] = arr[j] ;
            while(i<j && arr[i]<=pivot)  ++i;
            arr[j] = arr[i];
        }
        arr[i] = pivot;    //枢轴归位
        // 再判断是否需要继续，如果i>k，代表范围大了，减小范围
        //若果i<k代表我们的范围小了，需要再次划分
        if (i > k) return quick_select(arr, k, low, i - 1);
        if (i < k) return quick_select(arr, k, i + 1, high);
        vector<int> res;
        res.assign(arr.begin(), arr.begin() + k);   //返回前K个
        return res;
    }
};

414. 第三大的数

方法一：使用集合(默认排序)，且仅保存3个数

class Solution {
public:
    int thirdMax(vector<int> &nums) {
        set<int> s;
        for (int num : nums) {
            s.insert(num);
            if (s.size() > 3) {	//超过3个元素就删除其中最小的
                s.erase(s.begin());
            }
        }
        return s.size() == 3 ? *s.begin() : *s.rbegin();	//不足3个数就返回最大的(例二的情况)
    }
};

解法二：用三个指针，仅用一轮扫描就可以找到

class Solution {
public:
    int thirdMax(vector<int> &nums) {
        int *a = nullptr, *b = nullptr, *c = nullptr;
        for (int &num : nums) {
            if (a == nullptr || num > *a) {
                c = b;
                b = a;
                a = &num;
            } else if (*a > num && (b == nullptr || num > *b)) {
                c = b;
                b = &num;
            } else if (b != nullptr && *b > num && (c == nullptr || num > *c)) {
                c = &num;
            }
        }
        return c == nullptr ? *a : *c;
    }
};

215. 数组中的第K个最大元素(这个条件又比上面的苛刻一些了)

解法一：还是直接快排

解法二：快速选择

class Solution {
public:
    int quickSelect(vector<int>& a, int l, int r, int index) {
        int q = randomPartition(a, l, r);
        if (q == index) {
            return a[q];
        } else {
            return q < index ? quickSelect(a, q + 1, r, index) : quickSelect(a, l, q - 1, index);
        }
    }
    inline int randomPartition(vector<int>& a, int l, int r) {
        int i = rand() % (r - l + 1) + l;//引入随机化	快排的时间复杂度取决于划分
        swap(a[i], a[r]);
        return partition(a, l, r);
    }
    inline int partition(vector<int>& a, int l, int r) {//划分
        int x = a[r], i = l - 1;
        for (int j = l; j < r; ++j) {
            if (a[j] <= x) {
                swap(a[++i], a[j]);
            }
        }
        swap(a[i + 1], a[r]);
        return i + 1;
    }
    int findKthLargest(vector<int>& nums, int k) {
        srand(time(0));
        return quickSelect(nums, 0, nums.size() - 1, nums.size() - k);
    }
};

解法三：利用大根堆

class Solution {
public:
    void maxHeapify(vector<int>& a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a[i], a[largest]);
            maxHeapify(a, largest, heapSize);
        }
    }

​    void buildMaxHeap(vector<int>& a, int heapSize) {	//建堆操作
​        for (int i = heapSize / 2; i >= 0; --i) {
​            maxHeapify(a, i, heapSize);
​        } 
​    }

​    int findKthLargest(vector<int>& nums, int k) {
​        int heapSize = nums.size();
​        buildMaxHeap(nums, heapSize);
​        for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
​            swap(nums[0], nums[i]);
​            --heapSize;
​            maxHeapify(nums, 0, heapSize);
​        }
​        return nums[0];
​    }
};