本文学习之这篇博客:https://www.cnblogs.com/-Ackerman/
首先我们来看大数加法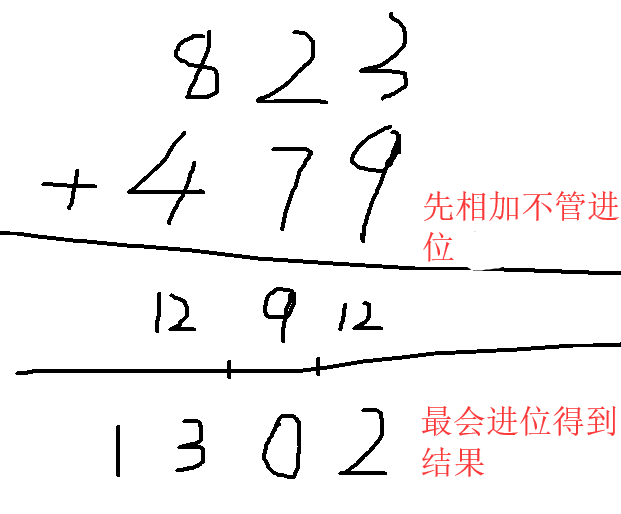
可以这样理解,先相加,再进位,当然我们这里全部用字符串来存储,看代码就懂了
#include<bits/stdc++.h> using namespace std; string BigAdd(string s1,string s2) { string anser; int len1=s1.length();//获取字符长度 int len2=s2.length(); int num1[100]={0},num2[100]={0};//这样可以很好解决前导0 for(int i=0;i<len1;i++) num1[len1-i-1]=s1[i]-'0';//逆序添加到num1中,即num1中是按照 个 十 百。。。 for(int i=0;i<len2;i++) num2[len2-i-1]=s2[i]-'0'; int lenth=len1>len2?len1:len2; for(int i=0;i<lenth;i++) { num1[i]+=num2[i];//各位加法 num1[i+1]+=num1[i]/10;//进位,将后小位进到大位上 num1[i]%=10;//进位后的余数保存到小位上 } if(!num1[lenth]) //去前导0
lenth--; for(int i=lenth;i>=0;i--) { anser+=num1[i]+'0'; } return anser;//将计算结果返回 } int main() { string a,b; while(cin>>a>>b) { cout<<BigAdd(a,b)<<endl; } return 0; }
如果你能理解大数加法,那么大数乘法和它其实在进位原理上相同,但需要明白乘法怎么算
我以98*23为例,答案=3*8+3*9*10+2*10*8+2*10*9*10,你可以自己验证我写的对不对
乘法的规律:即一个数的第i 位和另一个数的第j 位相乘所得的数,一定是要累加到结果的第i+j 位上。这里i, j 都是从右往左,从0 开始数。
即:ans[i+j] = a[i]*b[j];
#include<bits/stdc++.h> using namespace std; #define MAX 100 int x[MAX+10],y[MAX+10],z[MAX*2+10],i,j; string BigMultiply(string a,string b) { int len1=a.length(); int len2=b.length(); string anser; for(j=0,i=len1-1;i>=0;i--)//将字符串中字符转化为数字,并倒序储存 x[j++]=a[i]-'0';//这里加了个J比较方便 等同于上面大数加法的[len-i-1],看你理解那个容易 for(j=0,i=len2-1;i>=0;i--) y[j++]=b[i]-'0'; for(int i=0;i<len1;i++) { for(int j=0;j<len2;j++) { z[i+j]+=x[i]*y[j];// } } for(int i=0;i<2*MAX;i++) { if(z[i]>=10) //进位 { z[i+1]+=(z[i]/10); z[i]=z[i]%10; } } for(i=MAX*2;i>0;i--) //删除0的前缀 { if(z[i]==0) continue; else break; } for(;i>=0;i--) //倒序输出 anser+=z[i]+'0'; return anser; } int main() { string a,b; while(cin>>a>>b) { cout<<BigMultiply(a,b)<<endl; } return 0; }