大家好,今天我们来扯自动AC机AC自动机了。
I.前置知识
trie树。(那些说需要kmp的,不会也没事,不过还是会方便理解一点)。
II.用途
AC自动机可以在(O(Sigma|S|))的时间内预处理,并在(O(|S|))内求出一组模式串集在一个文本串中的出现次数。
换句话说,给你(n)个模式串(s_1)至(s_n),和一个文本串(t),我们可以在(O(|T|))时间将每个(s_i)对(t)做一次kmp。而用暴力的kmp是(O(|T|Sigma|S_i|))的。
III.操作
首先,我们建出一颗trie树。
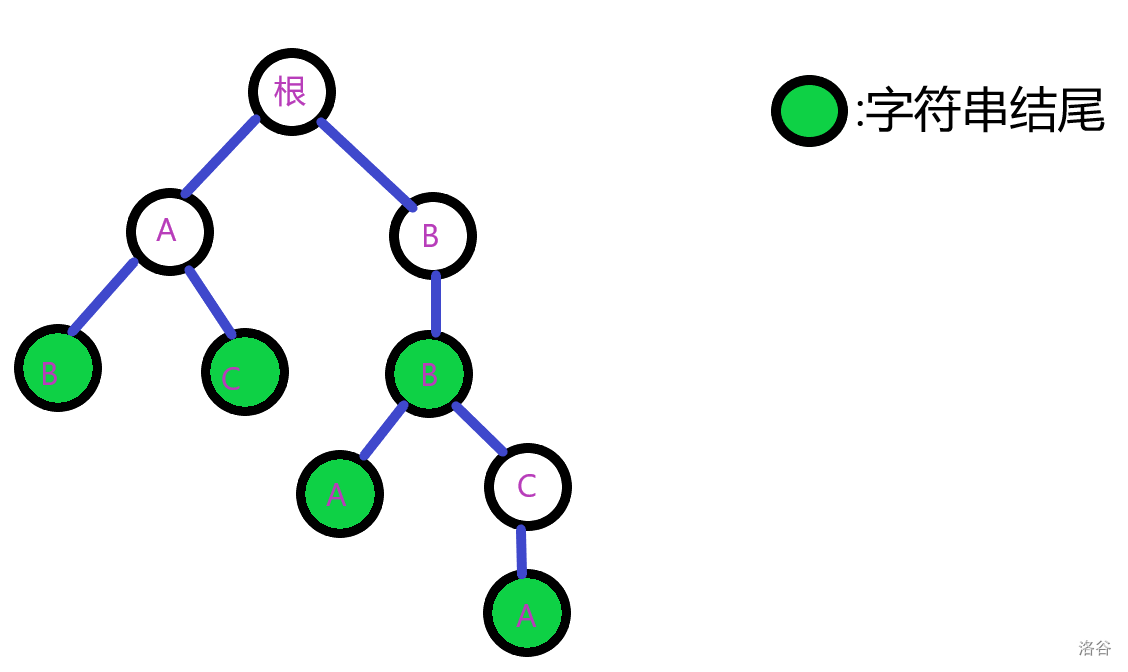
如果我们暴力匹配,失配就暴力回溯的话,复杂度甚至还不如暴力kmp。
借鉴kmp的(next)思想,如果失配,我们是不是可以略过重复部分,只做有用的匹配呢?
我们引出(fail)数组。这个神奇的数组的意思是:如果在节点(i)处失配了,我们可以直接跳到点(fail_i),避免回溯。
IV.求(fail)
显然,如果失配,我们希望这个(fail)的位置尽量更深一点,以加快匹配。
并且,(i)与(fail_i)必定要有相同的前缀,不然这次跳跃就是不合法的。
我们现在采取暴力bfs的方法求(fail)。
IV.i.根的子节点
显然,对于根的子节点,它们不可能有一个合法的(fail)。而由于深度足够浅,暴力回溯也没有问题。因此,我们将它们的(fail)全都指向根。之后,将它们入队。
另外,对于没有出现在trie树中的子节点,将它们全部设成指向根,即默认失配。
IV.ii.普通节点
我们取出队首节点,设为(x)。
枚举它的所有子节点:
IV.ii.1.已有节点(设为(y))
因为(x)与(fail_x)有共同的前缀,所以当前缀由(x)延伸到(y)时,(fail_x)也可以向相同方向延伸。
关键代码((t):trie数组,(ch):子节点编号,(fail):(fail)数组):
t[t[x].ch[i]].fail=t[t[x].fail].ch[i],q.push(t[x].ch[i]);
非常易记,因为刚好是内外互换。
IV.ii.2.空节点
默认直接失配,直接指向原本的(fail)。
关键代码:
t[x].ch[i]=t[t[x].fail].ch[i];
IV.iii.总代码
void build(){
for(int i=0;i<26;i++){
if(t[1].ch[i])q.push(t[1].ch[i]),t[t[1].ch[i]].fail=1;
else t[1].ch[i]=1;
}
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[x].ch[i])t[t[x].ch[i]].fail=t[t[x].fail].ch[i],q.push(t[x].ch[i]);
else t[x].ch[i]=t[t[x].fail].ch[i];
}
}
}
IV.iv.感性理解
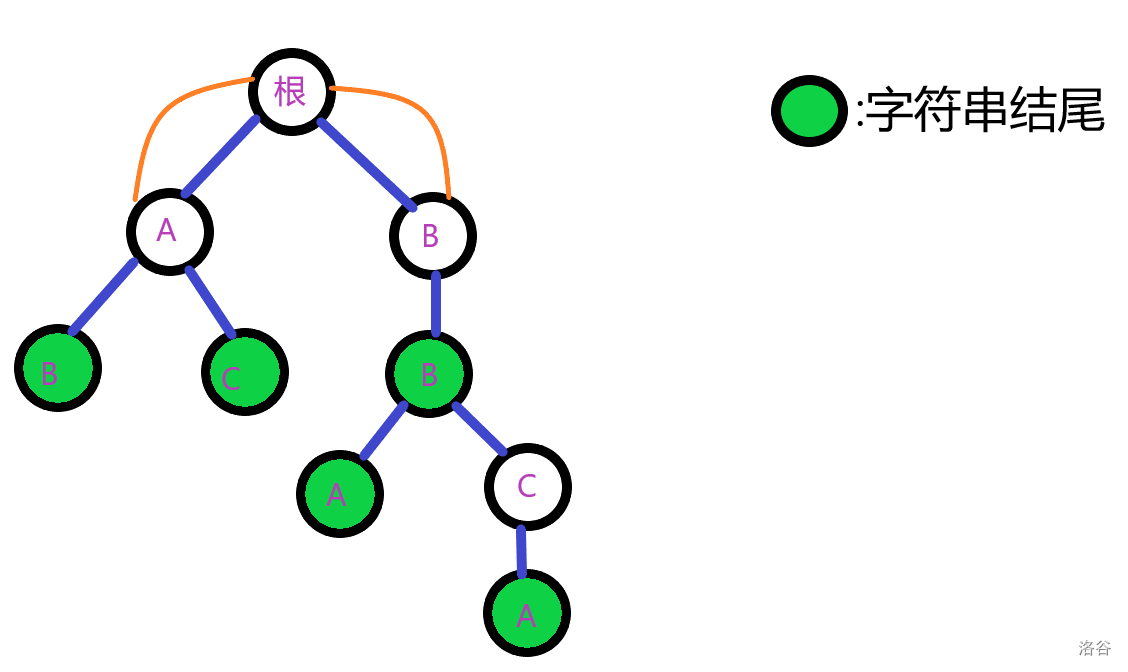
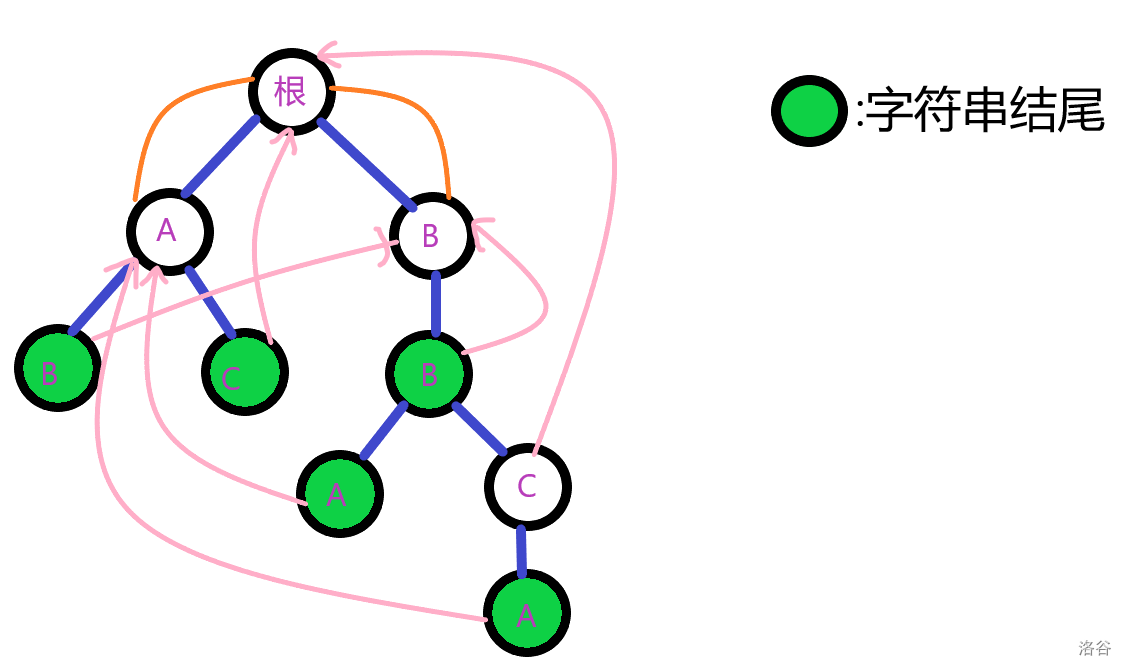
第一步,根的子节点(未出现节点未标出)入队。
现在,我们到了第(1)层(根为(0)层)的第一个节点(A)。
考虑它的儿子,第(2)层的第一个节点(B)。
它指向(A)的(fail)(根)的儿子(B)。
即有:
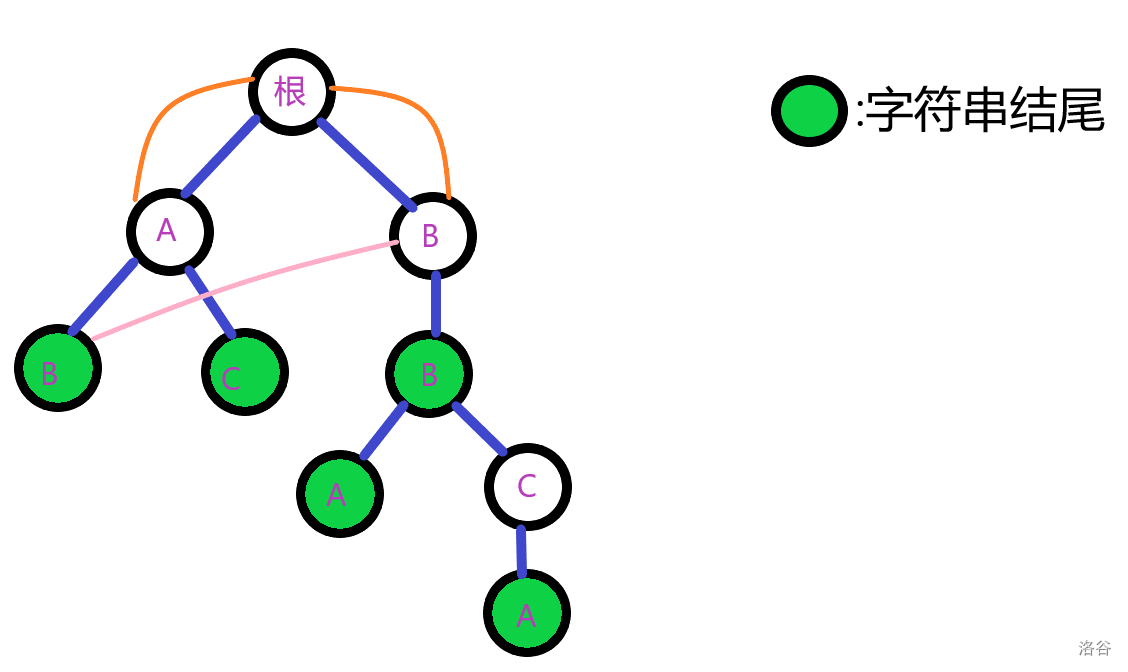
第(2)层的第一个节点(B)并无儿子,忽略它的操作。
考虑第(2)层的第二个节点(C)。
它指向根的儿子(C)。但是,这个(C)并不存在,它被暴力连到了根。
即有: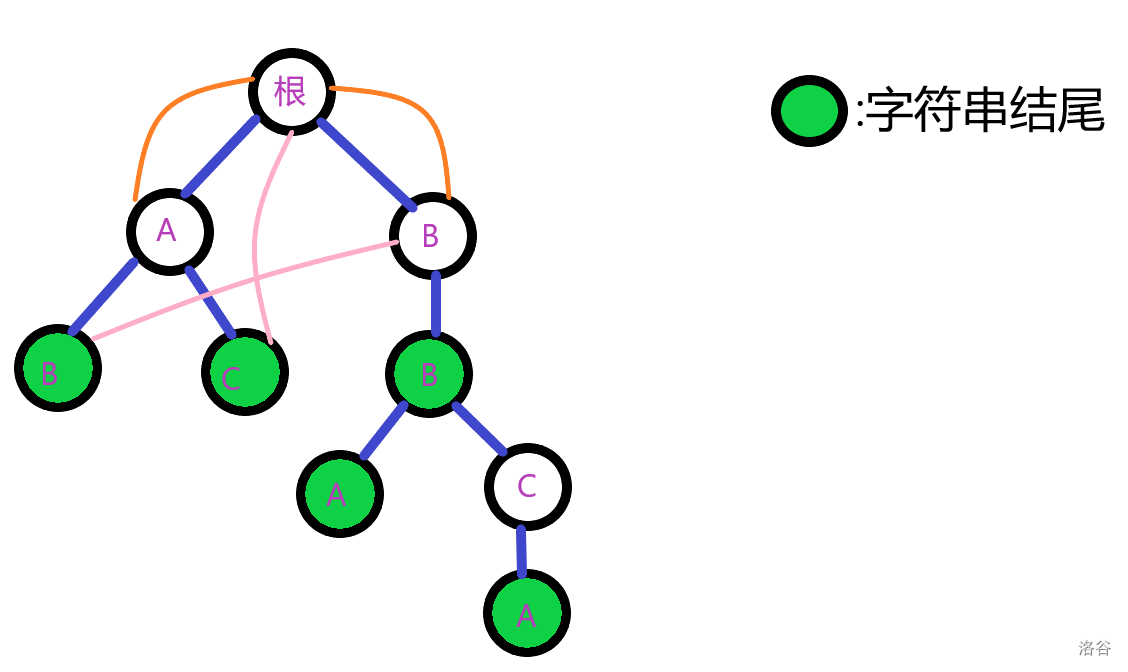
第(2)层的第一个节点(C)并无儿子,忽略它的操作。
考虑第(1)层的第二个节点(B)。
它唯一的儿子,第(2)层的第三个节点(B)。这个节点应指向根的(B)儿子——它的父亲,第(1)层的第二个节点(B)。
考虑第(3)层的第一个节点(A)。
它父亲的(fail)(第(1)层的第二个节点(B))并无(A)儿子。但是这个(A)儿子已经被赋成第(1)层的第一个节点(A)。可是是,这个第(1)层的第一个节点(A)也没有(A)儿子,则它被赋成了根(这个节点的(fail))的(A)儿子——第(1)层的第一个节点(A)。(也就是说,第(1)层的第一个节点(A)的(A)儿子是它自己!)
则第(3)层的第一个节点(A)的(fail)连向了第(1)层的第一个节点(A)。(好好理解一下!)
最后有:
V.匹配
不知道大家还记不记得我们一开始的结论:
我们引出(fail)数组。这个神奇的数组的意思是:如果在节点(i)处失配了,我们可以直接跳到点(fail_i),避免回溯。
然后我们就可以暴力跳了。
见代码:
void merge(){
int x=1;
for(int i=0;i<S;i++){
x=t[x].ch[s[i]-'a'];
for(int y=x;y!=1;y=t[y].fail)if(t[y].fin)occ[t[y].fin]++;
}
}
((fin):该节点是哪条字符串的结尾;(occ):统计答案的计数器)
为什么跳到一个节点,要对它所有的祖先(fail)也增加答案呢?
我也不知道。
其实是因为它所有的祖先(fail),当到达该节点时,也又出现了一次(因为(fail)是最长相同前缀)。
那为什么暴力跳就可以,不用担心失配呢?
因为所有未出现的节点,都在求(fail)时被我们重连了!
所以暴力跳就行。
VI.大礼包
(代码:【模板】AC自动机(加强版)
#include<bits/stdc++.h>
using namespace std;
int n,cnt,occ[210],S,mx;
char dict[210][100],s[1001000];
struct node{
int ch[26],fin,fail;
}t[20100];
void ins(int id){
int x=1;
for(int i=0;i<S;i++){
if(!t[x].ch[dict[id][i]-'a'])t[x].ch[dict[id][i]-'a']=++cnt;
x=t[x].ch[dict[id][i]-'a'];
}
t[x].fin=id;
}
queue<int>q;
void build(){
for(int i=0;i<26;i++){
if(t[1].ch[i])q.push(t[1].ch[i]),t[t[1].ch[i]].fail=1;
else t[1].ch[i]=1;
}
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[x].ch[i])t[t[x].ch[i]].fail=t[t[x].fail].ch[i],q.push(t[x].ch[i]);
else t[x].ch[i]=t[t[x].fail].ch[i];
}
}
}
void merge(){
int x=1;
for(int i=0;i<S;i++){
x=t[x].ch[s[i]-'a'];
for(int y=x;y!=1;y=t[y].fail)if(t[y].fin)occ[t[y].fin]++;
}
}
int main(){
while(scanf("%d",&n)){
if(!n)return 0;
memset(t,0,sizeof(t)),memset(occ,0,sizeof(occ)),mx=0,cnt=1;
for(int i=1;i<=n;i++)scanf("%s",dict[i]),S=strlen(dict[i]),ins(i);
build();
scanf("%s",s),S=strlen(s);
merge();
for(int i=1;i<=n;i++)mx=max(mx,occ[i]);
printf("%d
",mx);
for(int i=1;i<=n;i++)if(mx==occ[i])printf("%s
",dict[i]);
}
return 0;
}
VII.复杂度
(ins)函数单次复杂度为(O(|S|))。
(build)函数复杂度为(O(size)),其中(size)为trie树的大小(可看作(O(Sigma |S|)))。
(merge)函数最大单次复杂度为(O(size|S|))。
什么?不是说复杂度为(O(|S|))吗?那个(size)是从哪里冒出来的?
看这段代码。
for(int y=x;y!=1;y=t[y].fail)if(t[y].fin)occ[t[y].fin]++;
它更新了节点(x)的所有祖先(fail)。
明显,单次跳(fail),最少令层次上升一层。则暴力跳的话,复杂度为(O(dep)),其中(dep)为深度。
有没有什么办法优化它呢?
VIII.拓扑优化
因为(fail_i)的层次必定比(i)的层次要低,则依靠(fail)关系建成的(fail)图必定是一张(DAG)。
提到(DAG),我们一下就能想到拓扑排序。
因此我们可以在更新时,不暴力跳(fail),转而在(i)处打上标记。
最终用拓扑排序统计子树和。
IX.具体实现
(ins)完全相同。
(build)函数:
void build(){
for(int i=0;i<26;i++){
if(t[1].ch[i])t[t[1].ch[i]].fail=1,q.push(t[1].ch[i]),t[1].in++;
else t[1].ch[i]=1;
}
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[x].ch[i])t[t[x].ch[i]].fail=t[t[x].fail].ch[i],q.push(t[x].ch[i]),t[t[t[x].fail].ch[i]].in++;
else t[x].ch[i]=t[t[x].fail].ch[i];
}
}
}
唯一的区别就是在建(fail)时统计了每个节点的入度,便于拓扑排序。
(merge)函数:
void merge(){
int x=1;
for(int i=0;i<S;i++){
x=t[x].ch[s[i]-'a'];
t[x].tms++;
}
}
可以看到,暴力跳(fail)的操作已经被修改(tag)(代码中的(tms))取代。
最后是拓扑排序的(topo)函数:
void topo(){
for(int i=1;i<=cnt;i++)if(!t[i].in)q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
t[t[x].fail].tms+=t[x].tms;
t[t[x].fail].in--;
if(!t[t[x].fail].in)q.push(t[x].fail);
for(int i=0;i<t[x].fin.size();i++)occ[t[x].fin[i]]=t[x].tms;
}
}
总体就是个大拓扑。
关键就是可能有相同的字符串,因此用(vector)来存编号。另外在拓扑中顺便维护子树和
即关键代码
t[t[x].fail].tms+=t[x].tms;
X.大礼包II
(代码:【模板】AC自动机(二次加强版)
#include<bits/stdc++.h>
using namespace std;
int n,cnt=1,S,occ[200100];
char s[2001000];
struct AC_Automaton{
int ch[26],fail,tms,in;
vector<int>fin;
}t[200100];
void ins(int id){
int x=1;
for(int i=0;i<S;i++){
if(!t[x].ch[s[i]-'a'])t[x].ch[s[i]-'a']=++cnt;
x=t[x].ch[s[i]-'a'];
}
t[x].fin.push_back(id);
}
queue<int>q;
void build(){
for(int i=0;i<26;i++){
if(t[1].ch[i])t[t[1].ch[i]].fail=1,q.push(t[1].ch[i]),t[1].in++;
else t[1].ch[i]=1;
}
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<26;i++){
if(t[x].ch[i])t[t[x].ch[i]].fail=t[t[x].fail].ch[i],q.push(t[x].ch[i]),t[t[t[x].fail].ch[i]].in++;
else t[x].ch[i]=t[t[x].fail].ch[i];
}
}
}
void merge(){
int x=1;
for(int i=0;i<S;i++){
x=t[x].ch[s[i]-'a'];
t[x].tms++;
}
}
void topo(){
for(int i=1;i<=cnt;i++)if(!t[i].in)q.push(i);
while(!q.empty()){
int x=q.front();q.pop();
t[t[x].fail].tms+=t[x].tms;
t[t[x].fail].in--;
if(!t[t[x].fail].in)q.push(t[x].fail);
for(int i=0;i<t[x].fin.size();i++)occ[t[x].fin[i]]=t[x].tms;
}
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)scanf("%s",s),S=strlen(s),ins(i);
build();
scanf("%s",s),S=strlen(s);
merge();
topo();
for(int i=1;i<=n;i++)printf("%d
",occ[i]);
return 0;
}