Codeforces Round #416 (Div. 2)

A. Vladik and Courtesy

At regular competition Vladik and Valera won a and b candies respectively. Vladik offered 1 his candy to Valera. After that Valera gave Vladik 2 his candies, so that no one thought that he was less generous. Vladik for same reason gave 3 candies to Valera in next turn.

More formally, the guys take turns giving each other one candy more than they received in the previous turn.

This continued until the moment when one of them couldn’t give the right amount of candy. Candies, which guys got from each other, they don’t consider as their own. You need to know, who is the first who can’t give the right amount of candy.

Input

Single line of input data contains two space-separated integers a, b (1 ≤ a, b ≤ 109) — number of Vladik and Valera candies respectively.

Output

Pring a single line "Vladik’’ in case, if Vladik first who can’t give right amount of candy, or "Valera’’ otherwise.

Examples

input

1 1

output

Valera

input

7 6

output

Vladik

Note

Illustration for first test case:

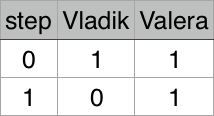
Illustration for second test case:

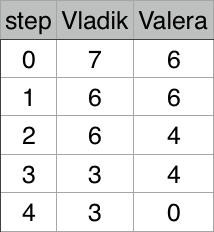
 题意：见图，文中的什么给对方瞎说的吧；

#include <bits/stdc++.h>

using namespace std;

int main()
{
    int a,b;
    scanf("%d%d",&a,&b);

    int k = 1;
    while(true) {
        a-=k;
        if(a<0) {
            printf("Vladik
");
            break;
        }
       // b+=k;
        k++;
        b-=k;
        if(b<0) {
            printf("Valera
");
            break;
        }
       // a+=k;
        k++;
    }

    return 0;
}

B. Vladik and Complicated Book

Vladik had started reading a complicated book about algorithms containing n pages. To improve understanding of what is written, his friends advised him to read pages in some order given by permutation P = [p1, p2, ..., pn], where pi denotes the number of page that should be read i-th in turn.

Sometimes Vladik’s mom sorted some subsegment of permutation P from position l to position r inclusive, because she loves the order. For every of such sorting Vladik knows number x — what index of page in permutation he should read. He is wondered if the page, which he will read after sorting, has changed. In other words, has px changed? After every sorting Vladik return permutation to initial state, so you can assume that each sorting is independent from each other.

Input

First line contains two space-separated integers n, m (1 ≤ n, m ≤ 104) — length of permutation and number of times Vladik's mom sorted some subsegment of the book.

Second line contains n space-separated integers p1, p2, ..., pn (1 ≤ pi ≤ n) — permutation P. Note that elements in permutation are distinct.

Each of the next m lines contains three space-separated integers li, ri, xi (1 ≤ li ≤ xi ≤ ri ≤ n) — left and right borders of sorted subsegment in i-th sorting and position that is interesting to Vladik.

Output

For each mom’s sorting on it’s own line print "Yes", if page which is interesting to Vladik hasn't changed, or "No" otherwise.

Examples

input

5 5
5 4 3 2 1
1 5 3
1 3 1
2 4 3
4 4 4
2 5 3

output

Yes
No
Yes
Yes
No

input

6 5
1 4 3 2 5 6
2 4 3
1 6 2
4 5 4
1 3 3
2 6 3

output

Yes
No
Yes
No
Yes

Note

Explanation of first test case:

1. [1, 2, 3, 4, 5] — permutation after sorting, 3-rd element hasn’t changed, so answer is "Yes".
2. [3, 4, 5, 2, 1] — permutation after sorting, 1-st element has changed, so answer is "No".
3. [5, 2, 3, 4, 1] — permutation after sorting, 3-rd element hasn’t changed, so answer is "Yes".
4. [5, 4, 3, 2, 1] — permutation after sorting, 4-th element hasn’t changed, so answer is "Yes".
5. [5, 1, 2, 3, 4] — permutation after sorting, 3-rd element has changed, so answer is "No".

题意：求重排一个区间后，其中的一个数字是否变位置；

大佬都写得主席树，不太会。

暴力了；

#include <bits/stdc++.h>

using namespace std;

const int maxn = 10000+5;



int d[maxn];
int a[maxn];

int main()
{
    //freopen("in.txt","r",stdin);
    int n,q;
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) {
        scanf("%d",&a[i]);
    }


    while(q--) {
        int l,r,x;
        scanf("%d%d%d",&l,&r,&x);
        int sum = 0;
        for(int i=l;i<=r;i++) {
            if(a[i]<a[x])
                sum++;
        }

        if(sum+l==x)
            puts("Yes");
        else puts("No");
    }



    return 0;
}

C. Vladik and Memorable Trip

Vladik often travels by trains. He remembered some of his trips especially well and I would like to tell you about one of these trips:

Vladik is at initial train station, and now n people (including Vladik) want to get on the train. They are already lined up in some order, and for each of them the city code ai is known (the code of the city in which they are going to).

Train chief selects some number of disjoint segments of the original sequence of people (covering entire sequence by segments is not necessary). People who are in the same segment will be in the same train carriage. The segments are selected in such way that if at least one person travels to the city x, then all people who are going to city x should be in the same railway carriage. This means that they can’t belong to different segments. Note, that all people who travel to the city x, either go to it and in the same railway carriage, or do not go anywhere at all.

Comfort of a train trip with people on segment from position l to position r is equal to XOR of all distinct codes of cities for people on the segment from position l to position r. XOR operation also known as exclusive OR.

Total comfort of a train trip is equal to sum of comfort for each segment.

Help Vladik to know maximal possible total comfort.

Input

First line contains single integer n (1 ≤ n ≤ 5000) — number of people.

Second line contains n space-separated integers a1, a2, ..., an (0 ≤ ai ≤ 5000), where ai denotes code of the city to which i-th person is going.

Output

The output should contain a single integer — maximal possible total comfort.

Examples

input

6
4 4 2 5 2 3

output

14

input

9
5 1 3 1 5 2 4 2 5

output

9

Note

In the first test case best partition into segments is: [4, 4] [2, 5, 2] [3], answer is calculated as follows: 4 + (2 xor5) + 3 = 4 + 7 + 3 = 14

In the second test case best partition into segments is: 5 1 [3] 1 5 [2, 4, 2] 5, answer calculated as follows: 3 + (2 xor 4) = 3 + 6 = 9.

题意：将一个区间是否分成几块，但是，每一块中的数字必须全部包括，将区间里面的数异或起来。

当时，我想到的状态dp(i,j)，其实大部分的dp(i,j) ，都可以转换为d(i)，那么预处理每一个值的左右区间，每一个区间的异或值。

状态的转移：

d(i) : 如果 i 是一个右端点，那么，划分为两个部分，注意中间的值，可以向前。

#include <bits/stdc++.h>

using namespace std;

const int maxn = 5000 + 5;

long long a[maxn];
int l[maxn],r[maxn];
long long st[maxn][maxn];
int vis[maxn];
long long dp[maxn];

int main()
{
    int n;
    scanf("%d",&n);

    for(int i=1;i<=n;i++) {
        scanf("%I64d",&a[i]);
        if(l[a[i]])
            l[a[i]]=min(l[a[i]],i);
        else
            l[a[i]]=i;
        if(r[a[i]])
            r[a[i]]=max(r[a[i]],i);
        else
            r[a[i]]=i;
    }

    for(int i=1; i<=n; i++)
    {
        memset(vis,0,sizeof(vis));
        st[i][i]=a[i];
        vis[a[i]]=1;
        for(int j=i+1; j<=n; j++)
        {
            if(!vis[a[j]])
            {
                st[i][j]=st[i][j-1]^a[j];
                vis[a[j]]=1;
            }
            else
            {
                st[i][j]=st[i][j-1];
            }
        }
    }


    dp[0]=0;
    for(int i=1; i<=n; i++)
    {
        int temp = a[i];
        if(i==r[temp])
        {
            int L=l[temp];
            int ok=1;
            for(int j=l[temp]+1; j<r[temp]; j++)
            {
                if(r[a[j]]>i)
                {
                    ok=0;
                    break;
                }
                L=min(l[a[j]],L);
            }
            if(ok)
                dp[i]=max(dp[i-1],dp[L-1]+st[L][i]);
            else
                dp[i]=dp[i-1];
        }
        else
            dp[i]=dp[i-1];
    }

    printf("%I64d
",dp[n]);


    return 0;
}