动量法

之前有讨论过梯度下降法：

 

参数迭代

 

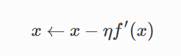
于是会产生问题，学习参数过小，模型很难到达最优点，而参数过大，某个参数会发散。

小批量随机梯度下降也讨论过了（线性回归的公式如下）：

 

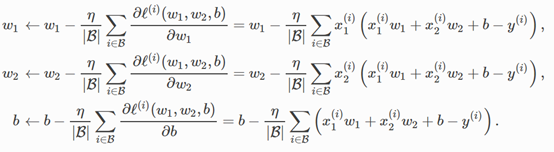
那么动量法呢？

简单地将梯度下降公式增加一个动量V，迭代公式如下：

 

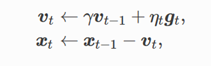
%matplotlib inline
from mxnet import nd
import numpy as np
import gluonbook as gb

def f_2d(x1,x2):
    return 0.1*x1**2 + 2*x2**2

eta  = 0.4

def gd_2d(x1,x2,s1,s2):
    return (x1 - eta *0.2*x1,x2-eta*4*x2,0,0)

def train_2d(trainer):
    x1,x2,s1,s2 = -5,-2,0,0
    results = [(x1,x2)]
    for i in range(20):
        x1,x2,s1,s2 = trainer(x1,x2,s1,s2)
        results.append((x1,x2))
    print('epoch %d, x1 %f, x2 %f' % (i + 1, x1, x2))
    return results

def show_trace_2d(f,results):
    gb.plt.plot(*zip(*results), '-o', color='#ff7f0e')
    x1, x2 = np.meshgrid(np.arange(-5.5, 1.0, 0.1), np.arange(-3.0, 1.0, 0.1))
    gb.plt.contour(x1, x2, f(x1, x2), colors='#1f77b4')
    gb.plt.xlabel('x1')
    gb.plt.ylabel('x2')


def momentum_2d(x1,x2,v1,v2):
    v1 = gamma * v1 + eta * 0.2 * x1
    v2 = gamma * v2 + eta * 4 * x2
    return x1 - v1,x2-v2,v1,v2


eta = 0.4
gamma = 0.5

show_trace_2d(f_2d,train_2d(momentum_2d))

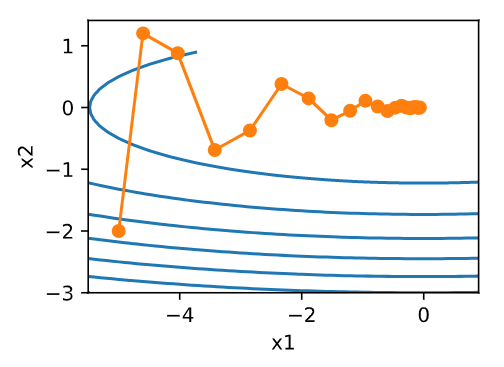
eta = 0.6
show_trace_2d(f_2d,train_2d(momentum_2d))

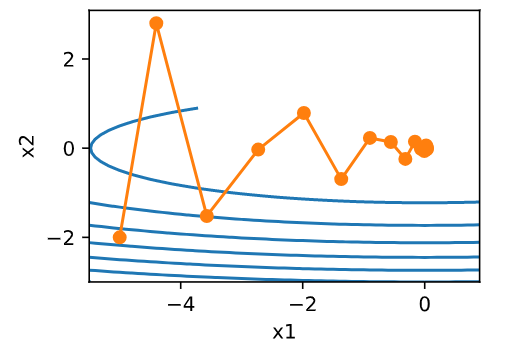
原理：

当前阶段 t （时间步t）的变量 yt 是上一个阶段 t-1 的变量 yt-1 与当前阶段的另一个变量xt的线性组合：

 

对yt展开：

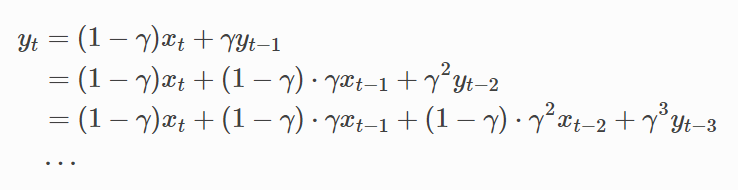
 容易知道（高等数学求极限）：

 

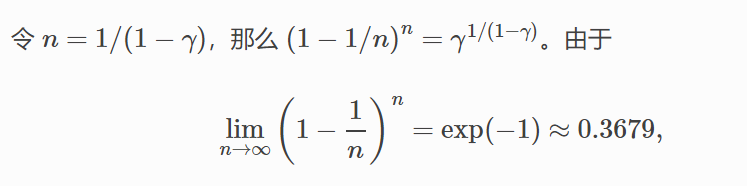
当gama 趋于 1 时，如0.95，也就是说：

即：

因此，常常将yt看做对最近 1/(1-gama) 个时间步的 xt 值得加权平均。例如，当 γ=0.95 时，yt 可以被看作是对最近 20 个时间步的 xt 值的加权平均；

当 γ=0.9 时，yt 可以看作是对最近 10 个时间步的 xt 值的加权平均。而且，离当前时间步 t 越近的 xt 值获得的权重越大（越接近 1）。

对动量法做同样的变形：

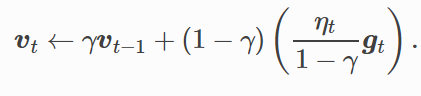
可以同样展开，即对序列

做了指数加权移动平均。

相比于小批量随机梯度下降，动量法每个阶段的自变量更新量近似于前者对应的最近1/1-gama个阶段做指数加权平均移动后除以1-gama。

 动量法：

就是每次状态转移时，不仅取决于当前梯度，并且要取决于过去的各个梯度在各个方向上是否一致