[LeetCode] Largest Rectangle in Histogram 解题思路

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

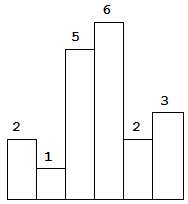
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.

For example,
Given height = [2,1,5,6,2,3],
return 10.

[ 解题思路 ]

问题： 求直方图中面积最大的矩形。

直方图中面积最大的矩形，必然以某一个柱作为高，左侧、右侧最近且矮于该柱的柱为宽边界。

考虑上面长度为 7 的直方图(图片来源)， {6, 2, 5, 4, 5, 2, 6}。面积最大矩形的是红框中的矩形，面积为 12 。

方案：

“i最大矩形”，表示为 i 柱为高，左侧、右侧最近且矮于该 i 柱的柱为宽边界的矩形。

"iLeft" , 表示左侧最近且矮于 i 柱的柱

"iRight", 表示右侧最近且矮于 i 柱的柱

 第一步，分别求出 n 个 “i最大矩形”，( i : 0->(n-1) )。第二步，找过第一步中最大值，即为原问题的解。

若每次单独求 i 柱的 "iLeft", "iRight"，则算法复杂度为 O(n*n)。可以利用栈 s ，巧妙地将时间复杂度降为 O(n)。

• 当栈为空 或 s.peak < h[i] 时，则将 i 压入栈顶。i++。
• 当 h[i] <= s.peak 时，对于 s.peak 柱来说， h[i] 为 "iRight",  栈中 s.peak 的前一个柱为 "iLeft"，则弹出 s.peak，并计算 s.peak 的 "i最大矩形"

    int largestRectangleArea(vector<int>& height) {

        int maxArea = 0;
        
        vector<int> stack;
        
        int i = 0;
        while ( i < height.size() ) {
            if (stack.size() == 0 || height[stack.back()] < height[i]) {
                stack.push_back(i);
                i++;
            }else{
                int tmpH = height[stack.back()];
                stack.pop_back();
                
                int tmpW = stack.empty() ? i : (i - stack.back() - 1);
                
                int area = tmpH * tmpW;
                maxArea = max(area, maxArea);
            }
        }
        
        while ( !stack.empty() ) {
            int tmpH = height[stack.back()];
            stack.pop_back();
            
            int tmpW = stack.empty() ? (int)height.size() : (int)height.size() - stack.back() - 1;
            
            int area = tmpH * tmpW;
            maxArea = max(area, maxArea);
        }
    
        return maxArea;
    }

参考资料：

Largest Rectangular Area in a Histogram | Set 2, GeeksforGeeks