写在前面
对于刚学树剖的同学比如我这种大大大蒟蒻来说,做这题会给你带来很大的提升:不仅可以对树剖有更深刻的理解,还可以更好的理解线段树,所以这是一道好题哦
为了更好懂,我一点一点说说思路吧
思路
首先这题题意不难懂,只有两个操作:区间颜色修改和区间查询颜色数量,我们分开来看:
区间查询颜色个数
这是这题的难点,弄懂了以后可以对线段树有个蛮大的提升吧
我们先把问题简化一下,假设这不是一棵树,只是一条连(已经树剖过了),给定每个元素的颜色,问有几段颜色(就是这题中颜色数量的定义),我们怎么做呢?
首先我们可以知道,为了保障时间复杂度,这题肯定是用线段树求解的,最先想到的是叶子节点的颜色个数为1,因为此时不存在有颜色会重复,按线段树的做法,现在要回溯求更大区间的颜色个数了,我们怎样求解呢?
其实分情况讨论一下就可以知道了:见下
第一种情况:
左区间:1231(颜色个数为4) 右区间:222(个数为1)
合并后:1231222(颜色个数为4+1=5)
这是第一种情况:没有重复
我们再来看第二种:
左区间:1231(颜色个数为4)右区间:121(个数为3)
合并后:1231121(颜色个数为4+3-1)
这就是第二种情况了,左区间的最后一个颜色和右区间的第一个颜色重合,也就重复了,所以总数减一
综上所述:我们用数组lc[ ]和rc[ ]表示区间左右颜色,线段树维护区间颜色总数,就可以解决链情况下的此问题了
int lc[maxn << 2];//这里要开4倍大小,因为是对应线段树节点的
int rc[maxn << 2];
void build(int id,int l,int r){
tree[id].l = l;
tree[id].r = r;
if(l == r){
tree[id].c = col[ori[l]];//赋值:叶子颜色
lc[id] = rc[id] = col[ori[l]];//赋值:区间左颜色和区间右颜色
tree[id].sum = 1;//颜色数为1
return ;
}
int mid = l + r >> 1;
build(lid,l,mid);
build(rid,mid + 1,r);
tree[id].sum = tree[lid].sum + tree[rid].sum;
if(rc[lid] == lc[rid])tree[id].sum -= 1;
lc[id] = lc[lid];
rc[id] = rc[rid];
}
void pushdown(int id){
if(tree[id].lazy != 0 && tree[id].l != tree[id].r){
int c = tree[id].lazy;
tree[lid].lazy = tree[rid].lazy = c;//粉刷
tree[lid].c = tree[rid].c = c;
lc[lid] = rc[lid] = lc[rid] = rc[rid] = c;//更新左右
tree[lid].sum = tree[rid].sum = 1;//粉刷完以后只有一种颜色了
tree[id].lazy = 0;
}
}
int query(int id,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
return tree[id].sum;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l){
return query(rid,l,r);
}
else if(mid >= r){
return query(lid,l,r);
}
else{
int ret = query(lid,l,mid) + query(rid,mid + 1,r);
if(rc[lid] == lc[rid])ret -= 1;
return ret;
}
}
值得注意的是:不要忘记大区间要继承小区间的左右端点颜色
树上查询颜色个数
我们的操作时基于树形的,所以树剖过后,我们树剖的查询函数要略作修改。
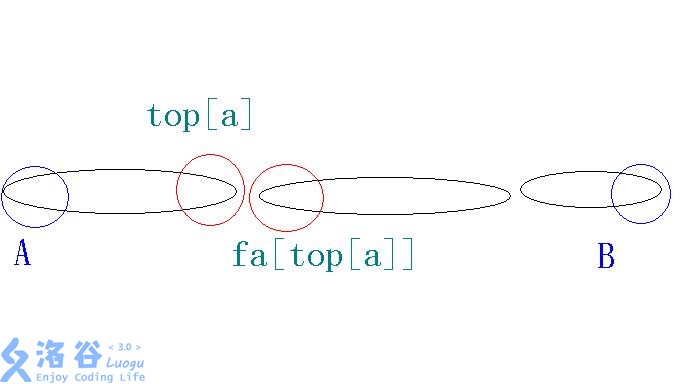
如上图:树剖就是把两点之间剖成了若干条链,我们还是要解决不同的链之间颜色重复问题。上图已经很明朗了:解决top[a]与fa[top[a]]颜色重复问题即可:
我写了个函数Qc来查询单点的颜色,其他学过树剖的应该不会太陌生:
int query(int id,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
return tree[id].sum;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l){
return query(rid,l,r);
}
else if(mid >= r){
return query(lid,l,r);
}
else{
int ret = query(lid,l,mid) + query(rid,mid + 1,r);
if(rc[lid] == lc[rid])ret -= 1;
return ret;
}
}
int Qc(int id,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
return tree[id].c;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l)return Qc(rid,l,r);
else return Qc(lid,l,r);
}
int Qsum(int x,int y){
int ans = 0,Cson,Cfa;//儿子的颜色,爸爸的颜色
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
ans += query(1,pos[top[x]],pos[x]);//累加答案
Cson = Qc(1,pos[top[x]],pos[top[x]]);
Cfa = Qc(1,pos[fa[top[x]]],pos[fa[top[x]]]);
if(Cson == Cfa)ans -= 1;//重复则答案减一
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
ans += query(1,pos[x],pos[y]);
return ans;
}
区间修改
与普通的树剖题修改无大异,注意线段树中的颜色数量更新即区间端点继承即可
void update(int id,int c,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
tree[id].c = c;
tree[id].lazy = c;
tree[id].sum = 1;
lc[id] = rc[id] = c;
return ;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l){
update(rid,c,l,r);
}
else if(mid >= r){
update(lid,c,l,r);
}
else{
update(lid,c,l,mid);
update(rid,c,mid + 1,r);
}
tree[id].sum = tree[lid].sum + tree[rid].sum;
if(rc[lid] == lc[rid])tree[id].sum -= 1;
lc[id] = lc[lid];
rc[id] = rc[rid];
}
void uprange(int x,int y,int c){
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
update(1,c,pos[top[x]],pos[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
update(1,c,pos[x],pos[y]);
}
AC代码
就不多提啦,祝大家天天AC!
(重要注释已经打在上面思路部分了,这里直接给代码)
#include<iostream>
#include<cstdio>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
int RD(){
int out = 0,flag = 1;char c = getchar();
while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
return flag * out;
}
const int maxn = 100019;
int num,na,nume,cnt;
int head[maxn];
struct Node{int v,nxt;}E[maxn * 2];
void add(int u,int v){
E[++nume].nxt = head[u];
E[nume].v = v;
head[u] = nume;
}
int size[maxn],wson[maxn],dep[maxn],fa[maxn],top[maxn],pos[maxn],ori[maxn];
int col[maxn];
void dfs1(int id,int F){
size[id] = 1;
for(int i = head[id];i;i = E[i].nxt){
int v = E[i].v;
if(v == F)continue;
dep[v] = dep[id] + 1;
fa[v] = id;
dfs1(v,id);
size[id] += size[v];
if(size[v] > size[wson[id]])wson[id] = v;
}
}
void dfs2(int id,int TP){
top[id] = TP;
pos[id] = ++cnt;
ori[cnt] = id;
if(!wson[id])return ;
dfs2(wson[id],TP);
for(int i = head[id];i;i = E[i].nxt){
int v = E[i].v;
if(v == fa[id] || v == wson[id])continue;
dfs2(v,v);
}
}
int lc[maxn << 2];
int rc[maxn << 2];
#define lid (id << 1)
#define rid (id << 1) | 1
struct sag_tree{
int l,r;
int sum,c;//区间颜色总数,叶子颜色
int lazy;//儿子的颜色
}tree[maxn << 2];
void build(int id,int l,int r){
tree[id].l = l;
tree[id].r = r;
if(l == r){
tree[id].c = col[ori[l]];//赋值:叶子颜色
lc[id] = rc[id] = col[ori[l]];//赋值:区间左颜色和区间右颜色
tree[id].sum = 1;//颜色数为1
return ;
}
int mid = l + r >> 1;
build(lid,l,mid);
build(rid,mid + 1,r);
tree[id].sum = tree[lid].sum + tree[rid].sum;
if(rc[lid] == lc[rid])tree[id].sum -= 1;
lc[id] = lc[lid];
rc[id] = rc[rid];
}
void pushdown(int id){
if(tree[id].lazy != 0 && tree[id].l != tree[id].r){
int c = tree[id].lazy;
tree[lid].lazy = tree[rid].lazy = c;//粉刷
tree[lid].c = tree[rid].c = c;
lc[lid] = rc[lid] = lc[rid] = rc[rid] = c;//更新左右
tree[lid].sum = tree[rid].sum = 1;//粉刷完以后只有一种颜色了
tree[id].lazy = 0;
}
}
void update(int id,int c,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
tree[id].c = c;
tree[id].lazy = c;
tree[id].sum = 1;
lc[id] = rc[id] = c;
return ;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l){
update(rid,c,l,r);
}
else if(mid >= r){
update(lid,c,l,r);
}
else{
update(lid,c,l,mid);
update(rid,c,mid + 1,r);
}
tree[id].sum = tree[lid].sum + tree[rid].sum;
if(rc[lid] == lc[rid])tree[id].sum -= 1;
lc[id] = lc[lid];
rc[id] = rc[rid];
}
int query(int id,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
return tree[id].sum;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l){
return query(rid,l,r);
}
else if(mid >= r){
return query(lid,l,r);
}
else{
int ret = query(lid,l,mid) + query(rid,mid + 1,r);
if(rc[lid] == lc[rid])ret -= 1;
return ret;
}
}
int Qc(int id,int l,int r){
pushdown(id);
if(tree[id].l == l && tree[id].r == r){
return tree[id].c;
}
int mid = tree[id].l + tree[id].r >> 1;
if(mid < l)return Qc(rid,l,r);
else return Qc(lid,l,r);
}
void uprange(int x,int y,int c){
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
update(1,c,pos[top[x]],pos[x]);
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
update(1,c,pos[x],pos[y]);
}
int Qsum(int x,int y){
int ans = 0,Cson,Cfa;
while(top[x] != top[y]){
if(dep[top[x]] < dep[top[y]])swap(x,y);
ans += query(1,pos[top[x]],pos[x]);
Cson = Qc(1,pos[top[x]],pos[top[x]]);
Cfa = Qc(1,pos[fa[top[x]]],pos[fa[top[x]]]);
if(Cson == Cfa)ans -= 1;
x = fa[top[x]];
}
if(dep[x] > dep[y])swap(x,y);
ans += query(1,pos[x],pos[y]);
return ans;
}
int main(){
num = RD();na = RD();
for(int i = 1;i <= num;i++)col[i] = RD();
int u,v;
for(int i = 1;i <= num - 1;i++){
u = RD();v = RD();
add(u,v);
add(v,u);
}
dfs1(1,-1);
dfs2(1,1);
build(1,1,num);
char ask;
int c;
for(int i = 1;i <= na;i++){
cin>>ask;
if(ask == 'Q'){
u = RD();v = RD();
printf("%d
",Qsum(u,v));
}
else{
u = RD();v = RD();c = RD();
uprange(u,v,c);
}
}
return 0;
}
最后,虽然dalao没帮啥忙,可是我是看大佬以前的代码查出错的,宣传一下大佬
最后当然是大家最喜欢的广告啦