最近在做项目时,用户不想使用平均值来判断当前数据状态,想用其他的方式来分析数据的变化状态,在查找了一些资料后,想使用灰色预测来进行数据的预测。下面的内容是从网上综合下来的,java代码也做了一点改动,以做记录和学习。
1.什么是灰色预测
灰色预测是一种对含有不确定因素的系统进行预测的方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
灰色时间序列预测,即用等时距观测到的反应预测对象特征的一系列数量值构造灰色预测模型,预测未来某一时刻的特征量,或达到某一特征量的时间。
2.灰色预测的数学建模
1).数据的检验与处理
为了保证GM(1,1)建模方法的可行性,需要对已知数据做必要的检验处理。
设原始数据列为 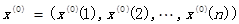 ,计算数列的级比
,计算数列的级比
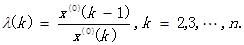
如果所有的级比都落在可容覆盖区间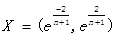
内,则数据列可以建立GM(1,1)模型且可以进行灰色预测。否则,对数据做适当的变换处理,如平移变换:取C使得数据列
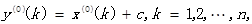 的级比都落在可容覆盖区间内。
的级比都落在可容覆盖区间内。
2).建立GM模型
不妨设 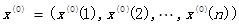 满足上面的要求,
满足上面的要求,
以它为数据列建立GM(1,1)模型 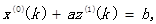
用回归分析求得a,b的估计值,于是相应的白化模型为
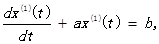
解为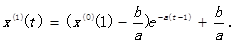
于是得到预测值 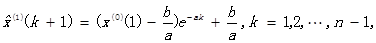
从而相应地得到预测值 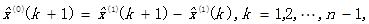
3).检验预测值
采用残差检验的方式进行检验。
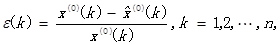
如果对所有的 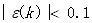 ,则认为达到较高的要求;
,则认为达到较高的要求;
否则,若对所有的 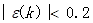 ,则认为达到一般的要求。
,则认为达到一般的要求。
3.java实现
public class GM { /** * @param args */ public static void main(String[] args) { double []arr={2.67,3.13,3.25,3.36,3.56,3.72,3.12,3.33,2.12}; System.out.println(gm(arr,3)); } public static double gm(double[] fs, int T) { // 预测模型函数 int size = fs.length; int tsize = fs.length - 1; double[] arr = fs;// 原始数组 double[] arr1 = new double[size];// 经过一次累加数组 double sum = 0; for (int i = 0; i < size; i++) { sum += arr[i]; arr1[i] = sum; } double[] arr2 = new double[tsize];// arr1的紧邻均值数组 for (int i = 0; i < tsize; i++) { arr2[i] = (double) (arr1[i] + arr1[i + 1]) / 2; } /* * * 下面建立 向量B和YN求解待估参数向量, 即求参数a,b */ /* * 下面建立向量B, B是5行2列的矩阵, 相当于一个二维数组。 */ double[][] B = new double[tsize][2]; for (int i = 0; i < tsize; i++) { for (int j = 0; j < 2; j++) { if (j == 1) B[i][j] = 1; else B[i][j] = -arr2[i]; } } /* * 下面建立向量YN */ double[][] YN = new double[tsize][1]; for (int i = 0; i < tsize; i++) { for (int j = 0; j < 1; j++) { YN[i][j] = arr[i + 1]; } } /* * B的转置矩阵BT,2行5列的矩阵 */ double[][] BT = new double[2][tsize]; for (int i = 0; i < 2; i++) { for (int j = 0; j < tsize; j++) { BT[i][j] = B[j][i]; } } /* * 将BT和B的乘积所得到的结果记为数组B2T,则B2T是一个2*2的矩阵 */ double[][] B2T = new double[2][2]; for (int i = 0; i < 2; i++) {// rows of BT { for (int j = 0; j < 2; j++)// cloums of B { for (int k = 0; k < tsize; k++)// cloums of BT=rows of B { B2T[i][j] = B2T[i][j] + BT[i][k] * B[k][j]; } } } } /* 下面求B2T的逆矩阵,设为B_2T,怎么适用于一般的矩阵? */ double[][] B_2T = new double[2][2]; B_2T[0][0] = (1 / (B2T[0][0] * B2T[1][1] - B2T[0][1] * B2T[1][0])) * B2T[1][1]; B_2T[0][1] = (1 / (B2T[0][0] * B2T[1][1] - B2T[0][1] * B2T[1][0])) * (-B2T[0][1]); B_2T[1][0] = (1 / (B2T[0][0] * B2T[1][1] - B2T[0][1] * B2T[1][0])) * (-B2T[1][0]); B_2T[1][1] = (1 / (B2T[0][0] * B2T[1][1] - B2T[0][1] * B2T[1][0])) * B2T[0][0]; /* * 根据以上所求的各已知量下面求待估参数的未知量a和b,待估向量矩阵等于B_2T*BT*YN * 下面我们分别求这些矩阵的乘积,首先求B_2T*BT,令B_2T*BT的乘积为A矩阵,则A就是一个2*5的矩阵 */ /* * * * * 下面先求A矩阵 */ double[][] A = new double[2][tsize]; for (int i = 0; i < 2; i++) {// rows of B_2T { for (int j = 0; j < tsize; j++)// cloums of BT { for (int k = 0; k < 2; k++)// cloums of B_2T=rows of BT { A[i][j] = A[i][j] + B_2T[i][k] * BT[k][j]; } } } } /* * * * 下面求A和YN矩阵的乘积,令乘积为C矩阵,则C就是一个2*1的矩阵 */ double[][] C = new double[2][1]; for (int i = 0; i < 2; i++) {// rows of A { for (int j = 0; j < 1; j++)// cloums of YN { for (int k = 0; k < tsize; k++)// cloums of A=rows of YN { C[i][j] = C[i][j] + A[i][k] * YN[k][j]; } } } } /* 根据以上所得则a=C[0][0],b=C[1][0]; */ double a = C[0][0], b = C[1][0]; int i = T;// 读取一个数值 double Y = (arr[0] - b / a) * Math.exp(-a * (i + 1)) - (arr[0] - b / a) * Math.exp(-a * i); return Y; } }