[JZOJ3509] 倒霉的小C

Description

　　小G最近迷上了岛国动漫《Angel Beats》，她为了画出一个更霸气的Angel Beats的logo，想了如下办法：

　　从（0，0）开始，画到（n，1），再从（n，1），画到（2*n，-1），再到（3*n，2），再到（4*n，-2），依此类推，即每次画出一个（n，(-1)^(i+1)*i）的向量，一共画出n个这样的向量。现在小G想让小C求出这个图形穿过了多少格点（坐标都是整数）。

　　由于小C想要认真地听他的数学课并且想自己在接力赛中因RP暴光而发生接力棒传错这类的糗事，所以这个问题就交给你啦。小G说，如果连你也解决不好，就把你的RP也吸光。

Input

　　输入文件中仅一行为一个整数n。

Output

　　输出文件中仅一行为一个数，表示穿过的格点数。

Sample Input

4

Sample Output

9

Data Constraint

　　对于20%的数据，满足：n<=100；

　　对于40%的数据，满足：n<=10^5；

　　对于60%的数据，满足：n<=10^7；

　　对于100%的数据，满足：n<=10^10。

Summary

　　

　　可以发现，每次向量经过的格点个数为gcd(i，n)，那么答案就等于Ans=1+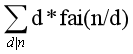=1+

#include<cstdio>
#include<cmath>
using namespace std;
long long ans,m;
long long find(long long x)
{
    long long sum=x,i=1;
    while (x>1)
    {
        i++;
        if (x%i==0)
        {
            sum-=sum/i;
            while (x%i==0)
                x=x/i;
        }
    }
    return sum;
}
int main()
{
    scanf("%lld",&m);
    ans=1;
    for (long long i=1;i<=(long long)sqrt((double) m);i++)
        if (m%i==0)
        {
            ans=ans+i*find(m/i);
            if (i*i!=m) 
                ans=ans+m/i*find(i);
        }
    printf("%lld",ans);
}