On one quiet day all of sudden Mister B decided to draw angle a on his field. Aliens have already visited his field and left many different geometric figures on it. One of the figures is regular convex n-gon (regular convex polygon with n sides).
That's why Mister B decided to use this polygon. Now Mister B must find three distinct vertices v1, v2, v3such that the angle  (where v2 is the vertex of the angle, and v1 and v3 lie on its sides) is as close as possible to a. In other words, the value
(where v2 is the vertex of the angle, and v1 and v3 lie on its sides) is as close as possible to a. In other words, the value 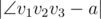 should be minimum possible.
should be minimum possible.
If there are many optimal solutions, Mister B should be satisfied with any of them.
First and only line contains two space-separated integers n and a (3 ≤ n ≤ 105, 1 ≤ a ≤ 180) — the number of vertices in the polygon and the needed angle, in degrees.
Print three space-separated integers: the vertices v1, v2, v3, which form  . If there are multiple optimal solutions, print any of them. The vertices are numbered from 1 to n in clockwise order.
. If there are multiple optimal solutions, print any of them. The vertices are numbered from 1 to n in clockwise order.
 if v1 < v2 < v3
if v1 < v2 < v3
= 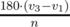 其他情况下
其他情况下
定好两个点,枚举第三个点就可以了

#include <bits/stdc++.h> #include <iomanip> typedef long long LL; using namespace std; #define SIZE 1000009 int n,a; int main(){ // freopen("test.in","r",stdin); cin >> n >> a; int base = n*a / 100; base = max(1,min(n-2,base)); int bk = base; for (int ck=3;ck<=n;ck++){ if (fabs(180*(ck-2)-n*a) < fabs(180*(bk-2)-n*a)){ bk = ck; } } cout << "2 1 " << bk; return 0; }
