Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.
A k-tree is an infinite rooted tree where:
- each vertex has exactly k children;
- each edge has some weight;
- if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, ..., k.
The picture below shows a part of a 3-tree.
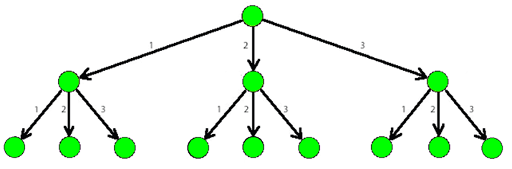
Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 (10^9 + 7).
A single line contains three space-separated integers: n, k and d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k).
Print a single integer — the answer to the problem modulo 1000000007 (10^9 + 7).
动归题,列出式子
设dp[i][0]是长度为i且其中没有大于等于d的边的方案数,dp[i][1]是长度为i且其中有至少一条大于等于d的边的方案数,则
i < d时
dp[i][0] = Σdp[i-a][0] (a∈[1,i]); dp[i][1] = 0
i >= d
dp[i][0] = Σdp[a][0] (a∈[i-d+1,i-1])
dp[i][1] = Σdp[a][0] (a∈[max(0,i-k),i-d]) + Σdp[i-a][1] (a∈[max(0,i-k),i-1])
本题就是要求dp[n][1]
然后注意下边界的初始化即可

#include<iostream> #include<cstring> #include<cstdio> #include <string> #include <sstream> #include <map> #include <cmath> #include <algorithm> #include <iomanip> #include <stack> #include <queue> #include <set> using namespace std; typedef long long LL; #define MOD 1000000007 LL dp[105][2]; LL n,k,d; int main(){ // freopen("test.in","r",stdin); cin >> n >> k >> d; memset(dp,0,sizeof(dp)); dp[1][0] = 1; dp[0][0] = 1; if (d == 1){ dp[1][1] = 1; dp[1][0] = 0; } for (int i=2;i<=n;i++){ if (i < d){ // dp[i][1] length = n weight >= d dp[i][1] = 0; // dp[i][0] = Σdp[i-a][0] (a∈[1,i]); for (int j=1;j<=i;j++){ dp[i][0] += dp[i-j][0]; dp[i][0] %= MOD; } } else { // dp[i][0] = Σdp[a][0] (a∈[i-d+1,i-1]) for (int j=i-d+1;j<=i-1;j++){ dp[i][0] += dp[j][0]; dp[i][0] %= MOD; } // dp[i][1] = Σdp[a][0] (a∈[max(0,i-k),i-d]) + Σdp[i-a][1] (a∈[max(0,i-k),i-1]) LL now; if (i-k>0){ now = i -k; } else { now = 0; } for (int j=now;j<=i-1;j++){ dp[i][1] += dp[j][1]; dp[i][1] %= MOD; } for (int j=now;j<=i-d;j++){ dp[i][1] += dp[j][0]; dp[i][1] %= MOD; } } } // for (int i=1;i<=n;i++){ // cout << dp[i][1] << " " << dp[i][0] << endl; // } cout << dp[n][1] % MOD; return 0; }
