hdu 5961 传递（暴力搜索）

我们称一个有向图G是传递的，当且仅当对任意三个不同的顶点a,,若G中有 一条边从a到b且有一条边从b到c ,则G中同样有一条边从a到c。

我们称图G是一个竞赛图，当且仅当它是一个有向图且它的基图是完全图。换句 话说，将完全图每条边定向将得到一个竞赛图。
下图展示的是一个有4个顶点的竞赛图。

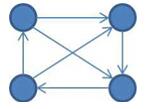
现在，给你两个有向图P = (V,Ep)和Q = (V,Ee)，满足:
1.   EP与Ee没有公共边；
2.  (V,Ep⋃Ee)是一个竞赛图。
你的任务是：判定是否P，Q同时为传递的。

 

Input

包含至多20组测试数据。
第一行有一个正整数，表示数据的组数。
对于每组数据，第一行有一个正整数n。接下来n行，每行为连续的n个字符，每 个字符只可能是’-’,’P’,’Q’中的一种。
∙如果第i行的第j个字符为’P’，表示有向图P中有一条边从i到j;
∙如果第i行的第j个字符为’Q’，表示有向图Q中有一条边从i到j;
∙否则表示两个图中均没有边从i到j。
保证1 <= n <= 2016，一个测试点中的多组数据中的n的和不超过16000。保证输入的图一定满足给出的限制条件。

 

Output

对每个数据，你需要输出一行。如果P! Q都是传递的，那么请输出’T’。否则， 请输出’N’ (均不包括引号)。

题意：就不解释反正都是中文。

就是遍历所有的边然后然后判断是否符合题目条件，单纯暴力挺卡时间的，可以用vector来存相邻边这样会快不少。

第一个用vector过的，第二个用结构体做的比较卡时间，边比较密集的话还是用结构体比较好点否则用vector比较快。

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
using namespace std;
const int M = 2e3 + 20;
char sl[M][M];
int n;
vector<int>q[M] , p[M];
void init() {
    for(int i = 0 ; i <= n ; i++) {
        q[i].clear();
        p[i].clear();
    }
}
int dfs(int x , vector<int> g[] , char cp) {
    int fi = g[x].size();
    for(int i = 0 ; i < fi ; i++) {
        int d = g[x][i];
        int se = g[d].size();
        for(int j = 0 ; j < se ; j++) {
            int k = g[d][j];
            if(sl[x][k] != cp) {
                return 0;
            }
        }
    }
    return 1;
}
int main()
{
    int t ;
    scanf("%d" , &t);
    while(t--) {
        scanf("%d" , &n);
        init();
        for(int i = 1 ; i <= n ; i++) {
            scanf("%s" , sl[i] + 1);
            for(int j = 1 ; j <= n ; j++) {
                if(sl[i][j] == 'P')
                    p[i].push_back(j);
                if(sl[i][j] == 'Q')
                    q[i].push_back(j);
            }
        }
        int flag = 0;
        for(int i = 1 ; i <= n ; i++) {
            if(!dfs(i , p , 'P')) {
                flag = 1;
                break;
            }
        }
        if(!flag) {
            for(int i = 1 ; i <= n ; i++) {
                if(!dfs(i , q , 'Q')) {
                    flag = 1;
                    break;
                }
            }
        }
        if(flag)
            printf("N
");
        else
            printf("T
");
    }
    return 0;
}

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int M = 3e3 + 10;
char sl[M][M];
int n , e , head1[M] , head2[M];
struct ss {
    int v , next;
}a[M * M] , b[M * M];
void init() {
    e = 0;
    for(int i = 0 ; i <= n + 1 ; i++) {
        head1[i] = -1;
        head2[i] = -1;
    }
}
void add(int x , int y , ss s[] , int head[]) {
    s[e].v = y;
    s[e].next = head[x];
    head[x] = e++;
}
int dfs(int t , char cp , int head[] , ss s[])
{
    for(int i = head[t] ; i != -1 ; i = s[i].next) {
        for(int j = head[s[i].v] ; j != -1 ; j = s[j].next) {
            if(sl[t][s[j].v] == cp)
                ;
            else
                return 0;
        }
    }
    return 1;
}
int main()
{
    int t ;
    scanf("%d" , &t);
    while(t--) {
        scanf("%d" , &n);
        init();
        for(int i = 1 ; i <= n ; i++) {
            scanf("%s" , sl[i] + 1);
            for(int j = 1 ; j <= n ; j++) {
                if(sl[i][j] == 'P')
                    add(i , j , a , head1);
                if(sl[i][j] == 'Q')
                    add(i , j , b , head2);
            }
        }
        int flag = 0;
        for(int i = 1 ; i <= n ; i++) {
            if(!dfs(i , 'P' , head1 , a)) {
                flag = 1;
                break;
            }
        }
        if(!flag) {
            for(int i = 1 ; i <= n ; i++) {
                if(!dfs(i , 'Q' , head2 , b)) {
                    flag = 1;
                    break;
                }
            }
        }
        if(flag)
            printf("N
");
        else
            printf("T
");
    }
    return 0;
}