【codeforces

目录

• description
• solution
• code
• details

---

description

给定字符串 (s)，需要在 (s) 中添加 (n) 个字符（可以添在开头或末尾）使得 (s) 变回文。

求最后可以得到本质不同的回文串。

problem link。

---

solution

定义 (f_{l,r,k}) 表示回文串的最前/最后 (k) 个字符匹配上 (s) 的 (1dots l-1) 与 (r+1dots|s|) 的方案数。
转移讨论 (s_l = s_r) 是否成立即可。最后依回文串长度的奇偶性分类讨论。

很明显可以矩乘，但是状态数达到 (O(|s|^2))，显然过不了。

那么出题人的意思就是让我们压缩状态。但是我们懒得找性质，所以直接用 BM 硬刚即可。

求出前 (A = 1000) 项的全局答案（不知道准确上界，不过1000项应该够了），然后 BM + 多项式取模可以做到 (O(|s|^2A + A^2log n))。下面的代码附的就是这个做法。

附一个BM算法流程的博客。关于为什么构造出来的一定最短，可以尝试阅读 mx 的集训队论文（由于我水平有限，没有读懂，所以就不附证明了）。

---

考虑合理合法地压缩状态。冷静分析一下，我们可以把状态和转移建图：

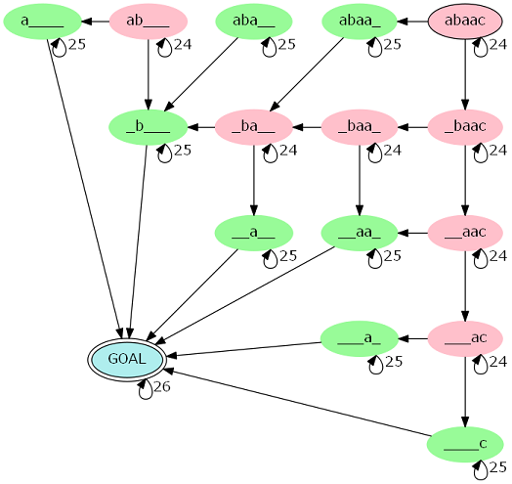
一条路径的方案数事实上只与这个路径上的红点个数有关（绿点个数可以根据红点个数算出来）。

那么先 dp 一遍求出有多少路径包含 (i) 个红点，再用这 (O(s)) 状态新建一个转移图：

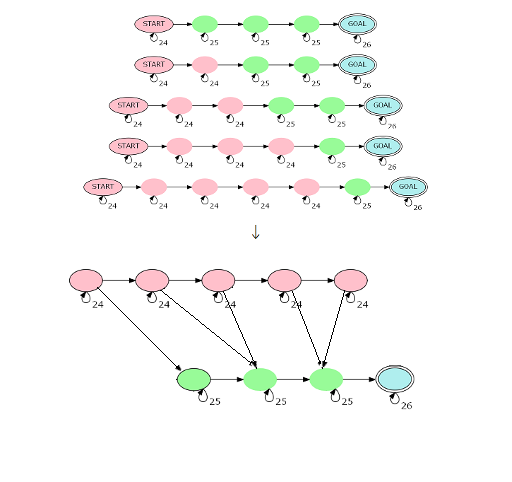
最后时间复杂度 (O(s^3log n))，听说有些卡常，需要利用三角矩阵的特性把矩阵乘法的部分优化一下。

由于我懒癌，所以就不写这种做法了。

---

code

#include <map>
#include <cstdio>
#include <cstring>
#include <cassert>
#include <algorithm>
using namespace std;

#define rep(i, x, n) for(int i=x;i<=n;i++)
#define per(i, x, n) for(int i=x;i>=n;i--)

const int MOD = 10007;
const int M = 1000;
const int N = 2*M;

inline int add(int x, int y) {x += y; return x >= MOD ? x - MOD : x;}
inline int sub(int x, int y) {x -= y; return x < 0 ? x + MOD : x;}
inline int mul(int x, int y) {return (int) (1LL * x * y % MOD);}
int mpow(int b, int p) {
	int r; for(r=1;p;p>>=1,b=mul(b,b))
		if( p & 1 ) r = mul(r, b);
	return r;
}

namespace linear_seq{

int t1[N + 5], t2[N + 5];
void pmul_mod(int *A, int *B, int *C, int *M, int n) {
	rep(i, 0, n - 1) t1[i] = A[i], t2[i] = B[i];
	per(i, 2*(n - 1), 0) C[i] = 0;
	rep(i, 0, n - 1) if( t1[i] )
		rep(j, 0, n - 1) C[i + j] = add(C[i + j], mul(t1[i], t2[j]));
	per(i, 2*(n - 1), n) if( C[i] )
		per(j, n, 0) C[i - j] = sub(C[i - j], mul(C[i], M[n - j]));
}

int b[N + 5], md[N + 5], bk;

void debug(int *A, int n) {
	rep(i, 1, bk) printf("%d%c", b[i], (i == bk) ? '
' : ' ');
	rep(i, bk + 1, n) {
		int d = A[i];
		rep(j, 1, bk) d = sub(d, mul(b[j], A[i - j]));
		assert(d == 0);
	}
}

int r[N + 5], c[N + 5], ck, rk, iv, nw;
void update(int x, int d) {
	if( nw == -1 || ck - x < rk - nw ) {
		rk = ck, nw = x, iv = mpow(d, MOD - 2);
		rep(i, 1, rk) r[i] = c[i];
	}
}

int f[N + 5], g[N + 5];
int get(int *A, int n, int m) {
//	if( m <= n ) return A[m];
	
	rk = bk = 0, nw = -1;
	rep(i, 1, n) {
		int d = A[i];
		rep(j, 1, bk) d = sub(d, mul(b[j], A[i - j]));
		if( d ) {
			rep(j, 1, bk) c[j] = b[j]; ck = bk;
			if( nw == -1 ) {
				bk = i; rep(j, 1, bk) b[j] = 0; 
			} else {
				int t = i - nw + rk;
				rep(j, bk + 1, t) b[j] = 0;
				bk = max(bk, t);
				
				int coef = mul(d, iv), p = i - nw;
				b[p] = add(b[p], coef);
				rep(j, 1, rk) b[p + j] = sub(b[p + j], mul(coef, r[j]));
			}
			update(i, d);
		}
	}
	
//	debug(A, n);
	
	rep(i, 1, bk) md[bk - i] = sub(0, b[i]); md[bk] = 1;
	f[1] = 1, g[0] = 1;
	for(;m;m>>=1,pmul_mod(f, f, f, md, bk))
		if( m & 1 ) pmul_mod(g, f, g, md, bk);
	
	int ret = 0;
	rep(i, 0, bk - 1) ret = add(ret, mul(g[i], A[i + 1]));
	return ret;
}

}

int f[2][M + 5][M + 5], a[M + 5];
char s[M + 5]; int n, len;
int main() {
	scanf("%s%d", s + 1, &n), len = strlen(s + 1), n += len;
	
	int res = 0; f[0][1][len] = 1;
	rep(i, 1, M) {
		rep(j, 1, len) rep(k, j, len)
			f[1][j][k] = f[0][j][k], f[0][j][k] = 0;
		res = mul(res, 26);
		rep(j, 1, len) {
			res = add(res, f[1][j][j]);
			f[0][j][j] = add(f[0][j][j], mul(f[1][j][j], 25));
			rep(k, j + 1, len) {
				if( s[j] == s[k] ) {
					f[0][j][k] = add(f[0][j][k], mul(25, f[1][j][k]));
					if( j + 1 == k ) res = add(res, f[1][j][k]);
					else f[0][j + 1][k - 1] = add(f[0][j + 1][k - 1], f[1][j][k]);
				} else {
					f[0][j][k] = add(f[0][j][k], mul(24, f[1][j][k]));
					f[0][j + 1][k] = add(f[0][j + 1][k], f[1][j][k]);
					f[0][j][k - 1] = add(f[0][j][k - 1], f[1][j][k]);
				}
			}
		}
		
		if( n & 1 ) {
			a[i] = mul(res, 26);
			rep(p, 1, len) a[i] = add(a[i], f[0][p][p]);
		} else a[i] = res;
	}
	
	printf("%d
", linear_seq::get(a, M, n / 2 - 1));
}

details

突然感觉到了BM是多么好用的一个东西。