咕咕咕。
这些题目倒不一定是我 3 月才做的,有可能是我之前做了现在才写的题解。
topcoder - SRM545D1L3:按位考虑,除非该位全是 1,否则两边必须各自至少有一个 0。容斥哪些位有一边全为 1,利用并查集算出结果。
#include <cstdio>
#include <vector>
using namespace std;
typedef long long ll;
class SetAndSet{
public:
int a[20][50], cnt[20], fa[20][50];
int find(int t, int x) {return fa[t][x] = (fa[t][x] == x ? x : find(t, fa[t][x]));}
bool unite(int t, int x, int y) {
int fx = find(t, x), fy = find(t, y);
if( fx != fy ) {
fa[t][fx] = fy;
return true;
}
else return false;
}
ll ans; int n;
void dfs(int d, int k, int f) {
if( d == 20 ) {
ans += f*((1LL << k) - 2);
return ;
}
if( d )
for(int i=0;i<n;i++) fa[d][i] = fa[d-1][i];
else for(int i=0;i<n;i++) fa[d][i] = i;
dfs(d + 1, k, f);
if( cnt[d] ) {
for(int i=1;i<cnt[d];i++)
if( unite(d, a[d][0], a[d][i]) ) k--;
dfs(d + 1, k, -f);
}
}
ll countandset(vector<int>A) {
n = A.size();
for(int i=0;i<20;i++) {
cnt[i] = 0;
for(int j=0;j<n;j++)
if( !((A[j] >> i) & 1) ) a[i][cnt[i]++] = j;
}
dfs(0, n, 1);
return ans;
}
};
ZOJ - 4064:考虑容斥,枚举哪些格子禁止覆盖。只有相邻禁止覆盖的格子才有贡献,所以记 dp[i][j] 表示最近一个禁止覆盖位置为 i,有 j 个可以选择覆盖的区间的方案数*容斥系数,转移随便做。本题有点卡常。
#include <cstdio>
const int MAXN = 100;
const int MOD = int(1E9) + 7;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=mul(b,b))
if( i & 1 ) ret = mul(ret, b);
return ret;
}
int f[MAXN + 5][MAXN*MAXN + 5], A[MAXN + 5], n, m;
void solve() {
scanf("%d%d", &n, &m);
for(int i=1;i<=n;i++)
scanf("%d", &A[i]);
A[n + 1] = f[0][0] = 1;
for(int i=0;i<=n;i++) {
int t = i*(i + 1)/2;
for(int j=0;j<=t;j++) {
if( f[i][j] ) {
for(int k=i+1;k<=n+1;k++) {
if( A[k] == 1 ) {
f[k][j+(k-i)*(k-i-1)/2] = add(f[k][j+(k-i)*(k-i-1)/2], f[i][j]);
break;
}
else if( A[k] == 2 )
f[k][j+(k-i)*(k-i-1)/2] = sub(f[k][j+(k-i)*(k-i-1)/2], f[i][j]);
}
}
}
}
int ans = 0, t = n*(n + 1)/2;
for(int i=0;i<=t;i++)
ans = add(ans, mul(f[n+1][i], pow_mod(i, m)));
for(int j=0;j<=n+1;j++)
for(int k=0;k<=t;k++)
f[j][k] = 0;
printf("%d
", ans);
}
int main() {
int T; scanf("%d", &T);
while( T-- ) solve();
}
topcoder - SRM583D1L3:min-max 容斥。枚举行的子集,根据贡献的表达式,对于列作个简单的背包。
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
class RandomPaintingOnABoard{
public:
int a[150][150], s[150], b[150], S, n, m;
double ans; long long dp[150*9];
void dfs(int d, int f, int t) {
if( d == n ) {
int tot; dp[tot = 0] = 1;
for(int i=0;i<m;i++) {
for(int j=tot+1;j<=tot+b[i];j++)
dp[j] = 0;
tot += b[i];
for(int j=tot;j>=b[i];j--)
dp[j] = dp[j] - dp[j-b[i]];
}
for(int i=0;i<=tot;i++)
if( i + t ) ans += 1.0*f*dp[i]*S/(i + t);
return ;
}
dfs(d + 1, f, t);
for(int i=0;i<m;i++) b[i] -= a[d][i], t += a[d][i];
dfs(d + 1, -f, t);
for(int i=0;i<m;i++) b[i] += a[d][i], t -= a[d][i];
}
double expectedSteps(vector<string>p) {
n = (int)p.size(), m = (int)p[0].size();
if( n < m ) {
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
a[i][j] = p[i][j] - '0', S += a[i][j];
}
else {
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
a[j][i] = p[i][j] - '0', S += a[j][i];
swap(n, m);
}
for(int j=0;j<m;j++)
for(int i=0;i<n;i++)
b[j] += a[i][j];
dfs(0, -1, 0);
return ans;
}
};
topcoder - 2016 TCO Algorithm Algo Final D1L3:首先做个 O(3^k) 的状压 dp 求出每个小图剖分成 i 条路径的方案数 f[i]。相当于 n 个图每个图都剖分成小路径然后将这些路径进行排列,并要求来源相同的路径不能相邻。不能相邻是一个经典容斥,路径全排列可以看作指数型生成函数的幂。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MOD = 998244353;
const int MAXN = 50000;
const int MAXK = 14;
const int MAXM = 2*MAXN*MAXK;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=mul(b,b))
if( i & 1 ) ret = mul(ret, b);
return ret;
}
class HamiltonianPaths{
private :
int dp1[14][1<<14], g[1<<14], dp2[15][1<<14], bts[1<<14], f[15];
int lowbit(int x) {return x & -x;}
void get1() {
int t = (1 << k);
for(int i=0;i<k;i++) dp1[i][1<<i] = 1;
for(int s=1;s<t;s++) {
if( s != lowbit(s) ) {
for(int i=0;i<k;i++)
if( (s >> i) & 1 ) {
int s2 = s ^ (1 << i);
for(int j=0;j<k;j++)
if( ((s2 >> j) & 1) && (G[j] & (1 << i)) )
dp1[i][s] = add(dp1[i][s], dp1[j][s2]);
}
}
for(int i=0;i<k;i++)
g[s] = add(g[s], dp1[i][s]);
}
dp2[0][0] = 1;
for(int s=1;s<t;s++) {
int s2 = s, q = lowbit(s); bts[s] = bts[s>>1] + (s & 1);
do {
if( s2 & q ) {
for(int p=1;p-1<=bts[s^s2]&&p<=bts[s];p++)
dp2[p][s] = add(dp2[p][s], mul(g[s2], dp2[p-1][s^s2]));
}
if( !s2 ) break;
s2 = (s2 - 1) & s;
}while( true );
}
for(int i=1;i<=k;i++) f[i] = dp2[i][t-1];
}
int a[15], b[15][15], c[15][15], fct[MAXM + 5];
void get2() {
for(int i=0;i<=k;i++) {
c[i][0] = 1;
for(int j=1;j<=i;j++)
c[i][j] = add(c[i-1][j], c[i-1][j-1]);
}
fct[0] = 1;
for(int i=1;i<=n*k;i++) fct[i] = mul(fct[i-1], i);
for(int i=1;i<=k;i++) {
for(int j=0;j<=i;j++)
for(int p=0;p<=i;p++)
b[j][p] = 0;
b[0][i] = 1;
for(int j=1;j<=i;j++) {
for(int p=1;p<=i;p++)
for(int q=1;q<=p;q++) {
int del = mul(mul(c[p][q], fct[q]), b[j-1][p]);
b[j][p-q] = (q & 1 ? add(b[j][p-q], del) : sub(b[j][p-q], del));
}
}
for(int j=1;j<=i;j++)
a[j] = add(a[j], mul(f[i], b[j][0]));
}
for(int i=1;i<=k;i++) a[i] = mul(a[i], pow_mod(fct[i], MOD - 2));
}
int w[22], iw[22], inv[MAXM + 5];
void ntt(int *A, int n, int type) {
for(int i=0,j=0;i<n;i++) {
if( i < j ) swap(A[i], A[j]);
for(int k=(n>>1);(j^=k)<k;k>>=1);
}
for(int i=1;(1<<i)<=n;i++) {
int s = (1 << i), t = (s >> 1);
int u = (type == 1 ? w[i] : iw[i]);
for(int j=0;j<n;j+=s) {
for(int k=0,p=1;k<t;k++,p=mul(p,u)) {
int x = A[j+k], y = mul(A[j+k+t], p);
A[j+k] = add(x, y), A[j+k+t] = sub(x, y);
}
}
}
if( type == -1 ) {
int iv = inv[n];
for(int i=0;i<n;i++)
A[i] = mul(A[i], iv);
}
}
int length(int n) {
int len; for(len = 1; len <= n; len <<= 1);
return len;
}
void init() {
for(int i=0;i<22;i++) {
w[i] = pow_mod(3, (MOD - 1) / (1 << i));
iw[i] = pow_mod(w[i], MOD - 2);
}
inv[1] = 1;
for(int i=2;i<=MAXM;i++)
inv[i] = sub(0, mul(MOD/i, inv[MOD%i]));
}
int A[MAXM + 5], B[MAXM + 5];
int get3() {
init();
int tmp = n, nA = 0, nB = k;
for(int i=1;i<=k;i++) B[i] = a[i];
A[0] = 1;
while( true ) {
if( tmp & 1 ) {
int len = length(nA + nB);
ntt(A, len, 1), ntt(B, len, 1);
for(int i=0;i<len;i++)
A[i] = mul(A[i], B[i]);
ntt(A, len, -1), ntt(B, len, -1);
nA += nB;
}
tmp >>= 1;
if( tmp == 0 ) break;
int len = length(nB * 2);
ntt(B, len, 1);
for(int i=0;i<len;i++)
B[i] = mul(B[i], B[i]);
ntt(B, len, -1);
nB *= 2;
}
int ans = 0;
for(int i=n;i<=n*k;i++)
ans = add(ans, mul(fct[i], A[i]));
return ans;
}
public :
int G[14], n, k;
int countPaths(int _k, vector<int>a, vector<int>b, int _n) {
int m = (int)a.size(); k = _k, n = _n;
for(int i=0;i<k;i++) G[i] = (1 << k) - 1;
for(int i=0;i<m;i++) G[a[i]] ^= (1 << b[i]), G[b[i]] ^= (1 << a[i]);
get1(), get2();
return get3();
}
};
atcoder - AGC005D:显然容斥,记 f[j] 表示有多少方案使得满足 |ai - i| = K 的 i 数量为 j,求出 f[j] 之后很简单。可以把相差为 K 的数字放在一起做 dp,然后全局再做个背包即可 O(n^2) 求 f。
#include <cstdio>
const int MOD = 924844033;
const int MAXN = 2000;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
int fct[MAXN + 5];
int f[2][2][MAXN + 5], h[2][2][MAXN + 5], g[MAXN + 5], t;
void init() {
fct[0] = 1;
for(int i=1;i<=MAXN;i++)
fct[i] = mul(fct[i-1], i);
g[t = 0] = 1;
}
void insert(int m) {
for(int i=0;i<=t;i++)
f[0][0][i] = f[0][1][i] = f[1][1][i] = 0, f[1][0][i] = g[i];
for(int i=1;i<=m;i++) {
for(int j=0;j<=t;j++)
for(int p=0;p<=1;p++)
for(int q=0;q<=1;q++)
h[p][q][j] = f[p][q][j], f[p][q][j] = 0;
t++, f[0][0][t] = f[0][1][t] = f[1][0][t] = f[1][1][t] = 0;
for(int j=0;j<=t;j++)
for(int p=0;p<=1;p++)
for(int q=0;q<=1;q++) {
f[q][0][j] = add(f[q][0][j], h[p][q][j]);
if( p == 0 ) {
f[q][0][j+1] = sub(f[q][0][j+1], h[p][q][j]);
f[q][1][j+1] = sub(f[q][1][j+1], h[p][q][j]);
}
else f[q][1][j+1] = sub(f[q][1][j+1], h[p][q][j]);
}
}
for(int i=0;i<=t;i++) g[i] = add(f[0][0][i], f[1][0][i]);
}
int a[MAXN + 5], N, K;
int main() {
init(), scanf("%d%d", &N, &K);
for(int i=1;i<=N;i++) a[i % K]++;
for(int i=0;i<K;i++) insert(a[i]);
int ans = 0;
for(int i=0;i<=N;i++)
ans = add(ans, mul(fct[N-i], g[i]));
printf("%d
", ans);
}
atcoder - AGC012D:如果 wi 与同颜色最小的 minw[ci] 相加 <= X,则可以把 wi 等价改成 w'i = minw[ci]。修改过后,如果一个元素的 wi 与异色最小的 wj 相加 <= Y,则认为这个元素是可动的。最终答案即这些可动的元素的可重排列。
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 200000;
const int MOD = int(1E9) + 7;
const int INF = (1<<30);
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=1LL*b*b%MOD)
if( i & 1 ) ret = 1LL*ret*b%MOD;
return ret;
}
int fct[MAXN + 5], ifct[MAXN + 5];
void init() {
fct[0] = 1;
for(int i=1;i<=MAXN;i++)
fct[i] = 1LL*i*fct[i-1]%MOD;
ifct[MAXN] = pow_mod(fct[MAXN], MOD - 2);
for(int i=MAXN-1;i>=0;i--)
ifct[i] = 1LL*ifct[i+1]*(i+1)%MOD;
}
int c[MAXN + 5], w[MAXN + 5], N, X, Y;
int mn[MAXN + 5], cnt[MAXN + 5];
int main() {
init(), scanf("%d%d%d", &N, &X, &Y);
for(int i=1;i<=N;i++) mn[i] = INF;
for(int i=1;i<=N;i++) {
scanf("%d%d", &c[i], &w[i]);
mn[c[i]] = min(mn[c[i]], w[i]);
}
for(int i=1;i<=N;i++)
if( mn[c[i]] + w[i] <= X )
w[i] = mn[c[i]];
int fmn = -1, smn = -1;
for(int i=1;i<=N;i++)
if( mn[i] != INF ) {
if( fmn == -1 || mn[fmn] > mn[i] )
smn = fmn, fmn = i;
else if( smn == -1 || mn[smn] > mn[i] )
smn = i;
}
int tot = 0;
for(int i=1;i<=N;i++) {
if( c[i] == fmn ) {
if( smn != -1 && w[i] + mn[smn] <= Y )
cnt[c[i]]++, tot++;
}
else {
if( w[i] + mn[fmn] <= Y )
cnt[c[i]]++, tot++;
}
}
int ans = fct[tot];
for(int i=1;i<=N;i++)
ans = 1LL*ans*ifct[cnt[i]]%MOD;
printf("%d
", ans);
}
atcoder - AGC013E:没有限制时,长度为 i 的权值对应的生成函数是 (F(x) = frac{(1-x)^3}{-x^3+2x^2-4x+1}),满足递推公式 (f_n = 4f_{n-1} - 2f_{n-2} + f_{n-3}),可以矩阵的幂描述 (f_n)。考虑容斥,枚举强制断开,并使用 dp。记上一次强制断开为 i 时权值为 dp[i]。朴素转移 O(n^2)。注意转移总是乘上矩阵的某个幂(对应某个 (f_i)),可以所有状态批量转移。
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MOD = int(1E9) + 7;
const int MAXM = 100000;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
struct matrix{
int m[3][3], r, c;
matrix() {memset(m, 0, sizeof m);}
friend matrix operator + (matrix A, matrix B) {
matrix C; C.r = A.r, C.c = B.c;
for(int i=0;i<C.r;i++)
for(int j=0;j<C.c;j++)
C.m[i][j] = add(A.m[i][j], B.m[i][j]);
return C;
}
friend matrix operator * (matrix A, matrix B) {
matrix C; C.r = A.r, C.c = B.c;
for(int i=0;i<C.r;i++)
for(int k=0;k<A.c;k++)
for(int j=0;j<C.c;j++)
C.m[i][j] = add(C.m[i][j], mul(A.m[i][k], B.m[k][j]));
return C;
}
friend matrix mpow(matrix A, int p) {
matrix ret; ret.r = ret.c = A.r;
for(int i=0;i<ret.r;i++)
for(int j=0;j<ret.c;j++)
ret.m[i][j] = (i == j);
while( p ) {
if( p & 1 ) ret = ret*A;
A = A*A;
p >>= 1;
}
return ret;
}
}A, B, S;
void init() {
A.r = A.c = 3;
A.m[0][0] = 4, A.m[0][1] = MOD - 2, A.m[0][2] = 1;
A.m[1][0] = A.m[2][1] = 1;
B.r = 3, B.c = 1;
B.m[0][0] = 5, B.m[1][0] = 1, B.m[2][0] = 0;
}
matrix get(int x) {
matrix R; R.r = R.c = 3;
R.m[0][0] = R.m[1][1] = R.m[2][2] = x;
return R;
}
int f[MAXM + 5], X[MAXM + 5], N, M;
int main() {
init(); scanf("%d%d", &N, &M);
for(int i=1;i<=M;i++) scanf("%d", &X[i]);
X[M + 1] = N, f[0] = -1, S = get(sub(0, f[0]));
for(int i=1;i<=M+1;i++) {
S = S * mpow(A, X[i] - X[i-1]);
f[i] = (S*B).m[2][0];
S = (S + get(sub(0, f[i])));
}
printf("%d
", (S*B).m[2][0]);
}
atcoder - AGC002F:按照最终序列中每种非零数字第一次出现的顺序从后往前 dp,最后乘上阶乘。记 dp[i][j] 表示第 i 种数字第一次出现在倒数第 j 个 0 之后,直接把第一个放在紧接着第 j 个 0 的后面,其他 K - 2 个在后面插空放,组合数算贡献。前缀和简单优化一下。特判 K = 1。
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 3000;
const int MAXM = MAXN*MAXN;
const int MOD = int(1E9) + 7;
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=1LL*b*b%MOD)
if( i & 1 ) ret = 1LL*ret*b%MOD;
return ret;
}
int fct[MAXM + 5], ifct[MAXM + 5];
int comb(int n, int m) {
return 1LL*fct[n]*ifct[m]%MOD*ifct[n-m]%MOD;
}
void init() {
fct[0] = 1;
for(int i=1;i<=MAXM;i++)
fct[i] = 1LL*fct[i-1]*i%MOD;
ifct[MAXM] = pow_mod(fct[MAXM], MOD - 2);
for(int i=MAXM-1;i>=0;i--)
ifct[i] = 1LL*ifct[i+1]*(i+1)%MOD;
}
int f[MAXN + 5][MAXN + 5];
int main() {
init();
int N, K; scanf("%d%d", &N, &K);
if( K == 1 ) {
puts("1");
return 0;
}
for(int i=1;i<=N;i++) f[1][i] = 1;
for(int i=2;i<=N;i++) {
for(int j=1;j<=i;j++) {
int m = (K - 1)*(i - 1) + j, n = K - 2;
f[i][j] = 1LL*f[i-1][j]*comb(n+m-1, n)%MOD;
}
for(int j=1;j<=N;j++)
f[i][j] = (f[i][j] + f[i][j-1]) % MOD;
}
printf("%lld
", 1LL*f[N][N]*fct[N]%MOD);
}
atcoder - AGC005F:连通块点数 = 总点数 - 不在连通块中的边数。对于一条边,它将整个图分为大小为 p 与 N - p 的两块,则它对于某个 K 的贡献为 ({p choose K} + {N - p choose K})。最终可得 (ans[K] = N{N choose K} - sum_{i=1}^{N-1}a_i{i choose K}),后面那个卷积一下就 OK 了。
#include <cstdio>
#include <algorithm>
using namespace std;
const int MOD = 924844033;
const int MAXN = 800000;
const int G = 5;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=mul(b,b))
if( i & 1 ) ret = mul(ret, b);
return ret;
}
int w[21], iw[21];
int fct[MAXN + 5], ifct[MAXN + 5], inv[MAXN + 5];
int comb(int n, int m) {
return mul(fct[n], mul(ifct[m], ifct[n-m]));
}
void init() {
for(int i=0;i<=20;i++) {
w[i] = pow_mod(G, (MOD - 1) / (1 << i));
iw[i] = pow_mod(w[i], MOD - 2);
}
inv[1] = 1;
for(int i=2;i<=MAXN;i++)
inv[i] = sub(0, mul(MOD/i, inv[MOD%i]));
fct[0] = 1;
for(int i=1;i<=MAXN;i++)
fct[i] = mul(fct[i-1], i);
ifct[MAXN] = pow_mod(fct[MAXN], MOD - 2);
for(int i=MAXN-1;i>=0;i--)
ifct[i] = mul(ifct[i+1], i+1);
}
int length(int n) {
int len; for(len = 1; len < n; len <<= 1);
return len;
}
void ntt(int *A, int n, int type) {
for(int i=0,j=0;i<n;i++) {
if( i < j ) swap(A[i], A[j]);
for(int k=(n>>1);(j^=k)<k;k>>=1);
}
for(int i=1;(1<<i)<=n;i++) {
int s = (1 << i), t = (s >> 1);
int u = (type == 1 ? w[i] : iw[i]);
for(int j=0;j<n;j+=s) {
for(int k=0,p=1;k<t;k++,p=mul(p,u)) {
int x = A[j+k], y = mul(A[j+k+t], p);
A[j+k] = add(x, y), A[j+k+t] = sub(x, y);
}
}
}
if( type == -1 ) {
int iv = inv[n];
for(int i=0;i<n;i++)
A[i] = mul(A[i], iv);
}
}
struct edge{
int to; edge *nxt;
}edges[MAXN + 5], *adj[MAXN + 5], *ecnt = edges;
void addedge(int u, int v) {
edge *p = (++ecnt);
p->to = v, p->nxt = adj[u], adj[u] = p;
p = (++ecnt);
p->to = u, p->nxt = adj[v], adj[v] = p;
}
int a[MAXN + 5], b[MAXN + 5], N;
int dfs(int x, int f) {
int ret = 1;
for(edge *p=adj[x];p;p=p->nxt) {
if( p->to == f ) continue;
int t = dfs(p->to, x);
a[t]++, a[N - t]++, ret += t;
}
return ret;
}
int main() {
init();
scanf("%d", &N);
for(int i=1;i<N;i++) {
int u, v; scanf("%d%d", &u, &v);
addedge(u, v);
}
dfs(1, 0);
for(int i=0;i<=N;i++) a[i] = mul(a[i], fct[i]), b[i] = ifct[i];
for(int i=1,j=N;i<j;i++,j--) swap(a[i], a[j]);
int len = length(2*N + 1);
ntt(a, len, 1), ntt(b, len, 1);
for(int i=0;i<len;i++) a[i] = mul(a[i], b[i]);
ntt(a, len, -1);
for(int i=1,j=N;i<j;i++,j--) swap(a[i], a[j]);
for(int i=1;i<=N;i++)
printf("%d
", sub(mul(comb(N, i), N), mul(a[i], ifct[i])));
}
atcoder - AGC016F:问题等价于 1 号点与 2 号点 sg 函数值不相等。从小到大不好,我们从大到小做。记 dp[s] 表示集合 s 合法方案数,每次加入一个 sg 最小的子集 t(t 中不能同时有 1 与 2)。转移讨论一下就 O(k*3^k)。
#include <cstdio>
#include <algorithm>
using namespace std;
const int MOD = int(1E9) + 7;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
bool check(int s) {return (s & 1) + ((s >> 1) & 1) == 2;}
int lowbit(int x) {return (x & -x);}
int f[1 << 15], g[1 << 15], bts[1 << 15], lg[1 << 15], pw2[20];
int G[15], N, M, S;
int main() {
scanf("%d%d", &N, &M), S = (1 << N);
for(int i=1;i<=M;i++) {
int x, y; scanf("%d%d", &x, &y), x--, y--;
G[x] |= (1 << y);
}
f[0] = pw2[0] = 1;
for(int i=0;i<N;i++) lg[1 << i] = i;
for(int i=1;i<=N;i++) pw2[i] = mul(2, pw2[i-1]);
for(int s=1;s<S;s++) bts[s] = bts[s >> 1] + (s & 1);
for(int s=0;s<S;s++) {
for(int s2=s;s2;s2=s&(s2-1)) {
if( check(s2) ) continue;
int s3 = (s ^ s2), p = s2, del = f[s3];
while( p ) {
int q = lowbit(p);
del = mul(del, pw2[bts[G[lg[q]] & s3]]);
p ^= q;
}
p = s3;
while( p ) {
int q = lowbit(p);
del = mul(del, sub(pw2[bts[G[lg[q]] & s2]], 1));
p ^= q;
}
f[s] = add(f[s], del);
}
}
printf("%d
", f[S - 1]);
}
topcoder - SRM620D1L3:把行、列、唯一分解后质数的幂都看成 01 变量,则每个点就是一个向量。题目所说的相当于向量异或得到某个值的方案数,线性基模板:如果能异或出来,答案为 2^(n*n - 线性基大小)。
#include <cstdio>
#include <vector>
#include <bitset>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
const int MOD = 1000000007;
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=1LL*b*b%MOD)
if( i & 1 ) ret = 1LL*ret*b%MOD;
return ret;
}
int siz; bitset<4000>b[4000], t;
void insert(int n) {
for(int i=n-1;i>=0;i--) {
if( t[i] ) {
if( b[i].any() )
t ^= b[i];
else {
b[i] = t, siz++;
return ;
}
}
}
}
bool check(int n) {
for(int i=n-1;i>=0;i--) {
if( t[i] ) {
if( b[i].any() )
t ^= b[i];
else return false;
}
}
return true;
}
class PerfectSquare{
public:
vector<int>A, B[400];
int ways(vector<int>x) {
int m = x.size(), n = sqrt(m);
for(int i=0;i<m;i++) {
int p = x[i], sq = sqrt(x[i]);
for(int j=2;j<=sq;j++) {
int pw = 0;
if( p % j == 0 ) {
while( p % j == 0 )
p /= j, pw++;
if( pw & 1 ) A.push_back(j), B[i].push_back(j);
}
}
if( p != 1 ) A.push_back(p), B[i].push_back(p);
}
sort(A.begin(), A.end());
int cnt = unique(A.begin(), A.end()) - A.begin(), tmp = cnt;
for(int i=0;i<m;i++)
for(int j=0;j<B[i].size();j++)
B[i][j] = lower_bound(A.begin(), A.begin() + cnt, B[i][j]) - A.begin();
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++)
B[i*n + j].push_back(cnt);
cnt++;
}
for(int i=0;i<n;i++) {
for(int j=0;j<n;j++)
B[j*n + i].push_back(cnt);
cnt++;
}
for(int i=0;i<m;i++) {
t = 0;
for(int j=0;j<B[i].size();j++)
t[B[i][j]] = 1;
insert(cnt);
}
t = 0;
for(int i=tmp;i<cnt;i++)
t[i] = 1;
if( check(cnt) ) return pow_mod(2, m - siz);
else return 0;
}
};
bzoj - 5469:定义 dp[i][j] 表示如果 i 的上级的 wk = j 时,i 子树内能取到的最优值。朴素做法 O(n^2),注意到 dp[i][j] 被划分成子树大小个块,考虑用平衡树启发式合并优化,每个点存一个段的 dp 值。只需支持子树加 + 插入点。
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <iostream>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
#define mp make_pair
#define fi first
#define se second
const int MAXN = 400000;
struct treap{
struct node{
int key, val, tag;
ull pri; node *ch[2];
}pl[MAXN + 5], *NIL;
typedef pair<node*, node*> Droot;
queue<node*>que;
ull get_rand() {
ull p = rand() << 16 | rand();
ull q = rand() << 16 | rand();
return p << 16 | q;
}
treap() {
NIL = pl; NIL->key = NIL->val = 0;
NIL->ch[0] = NIL->ch[1] = NIL;
for(int i=1;i<=MAXN;i++)
que.push(pl + i);
}
node *newnode(int k, int v) {
node *p = que.front(); que.pop();
p->key = k, p->val = v, p->pri = get_rand();
p->tag = 0, p->ch[0] = p->ch[1] = NIL;
return p;
}
void maintain(node *x, int k) {
if( x == NIL ) return ;
x->val += k, x->tag += k;
}
void pushdown(node *x) {
if( x->tag ) {
maintain(x->ch[0], x->tag);
maintain(x->ch[1], x->tag);
x->tag = 0;
}
}
node *merge(node *x, node *y) {
if( x == NIL ) return y;
if( y == NIL ) return x;
if( x->pri < y->pri ) {
pushdown(x);
x->ch[1] = merge(x->ch[1], y);
return x;
}
else {
pushdown(y);
y->ch[0] = merge(x, y->ch[0]);
return y;
}
}
Droot split(node *x, int k) {
if( x == NIL ) return mp(NIL, NIL);
pushdown(x);
if( x->key < k ) {
Droot p = split(x->ch[1], k);
x->ch[1] = p.fi;
return mp(x, p.se);
}
else {
Droot p = split(x->ch[0], k);
x->ch[0] = p.se;
return mp(p.fi, x);
}
}//key < k; key >= k
void erase(node *&x) {
que.push(x), x = merge(x->ch[0], x->ch[1]);
}
node *minmax(node *x, int d) {
node *y = x;
while( y->ch[d] != NIL )
pushdown(y), y = y->ch[d];
return y;
}
Droot get(node *x, int k) {
Droot p = split(x, k + 1); node *z = minmax(p.fi, 1);
if( z->key != k )
p.fi = merge(p.fi, newnode(k, minmax(p.se, 0)->val));
return p;
}
node *add(node *x, int k, int v) {
Droot p = get(x, k); maintain(p.fi, v);
return merge(p.fi, p.se);
}
int query(node *&x, int k) {
Droot p = split(x, k); node *z = minmax(p.se, 0);
int ret = z->val; x = merge(p.fi, p.se);
return ret;
}
node *update(node *x, int k, int v) {
Droot p = get(x, k); node *z = minmax(p.fi, 1);
if( z->val < v ) {
do {
Droot q = split(p.fi, z->key);
erase(q.se), p.fi = q.fi, z = minmax(p.fi, 1);
}while( z->val < v && z != NIL );
p.fi = merge(p.fi, newnode(k, v));
}
return merge(p.fi, p.se);
}
void debug(node *x) {
if( x == NIL ) return ;
pushdown(x);
debug(x->ch[0]);
printf("%2d : (%2d, %2d) ", x - pl, x->ch[0] - pl, x->ch[1] - pl);
printf("%2d %2d %2d
", x->key, x->val, x->tag);
debug(x->ch[1]);
}
}T;
typedef pair<treap::node*, treap::node*> Droot;
struct edge{
int to; edge *nxt;
}edges[MAXN + 5], *adj[MAXN + 5], *ecnt = edges;
void addedge(int u, int v) {
edge *p = (++ecnt);
p->to = v, p->nxt = adj[u], adj[u] = p;
}
int siz[MAXN + 5], hvy[MAXN + 5];
void dfs1(int x) {
hvy[x] = 0, siz[x] = 1;
for(edge *p=adj[x];p;p=p->nxt) {
dfs1(p->to), siz[x] += siz[p->to];
if( siz[p->to] > siz[hvy[x]] )
hvy[x] = p->to;
}
}
treap::node *a[MAXN + 5]; int cnt;
void get(treap::node *x) {
if( x == T.NIL ) return ;
T.pushdown(x);
get(x->ch[0]), a[++cnt] = x, get(x->ch[1]);
}
int w[MAXN + 5]; treap::node *rt[MAXN + 5];
void dfs2(int x) {
if( !hvy[x] )
rt[x] = T.newnode(w[x], 1);
else {
dfs2(hvy[x]), rt[x] = rt[hvy[x]];
for(edge *p=adj[x];p;p=p->nxt) {
if( p->to == hvy[x] ) continue;
dfs2(p->to); cnt = 0, get(rt[p->to]);
int lst = 0;
for(int i=cnt;i>=1;i--) {
rt[x] = T.add(rt[x], a[i]->key, a[i]->val - lst);
lst = a[i]->val, T.erase(a[i]);
}
}
int f = T.query(rt[x], w[x]) + 1;
rt[x] = T.update(rt[x], w[x], f);
}
/*
printf("%2d : %2d
", x, w[x]);
for(edge *p=adj[x];p;p=p->nxt)
printf("%2d ", p->to);
*/
}
int main() {
srand(20041112);
int n; scanf("%d", &n);
for(int i=1;i<=n;i++) scanf("%d", &w[i]);
for(int i=2;i<=n;i++) {
int v; scanf("%d", &v);
addedge(v, i);
}
dfs1(1), dfs2(1), printf("%d
", T.minmax(rt[1], 0)->val);
}
bzoj - 3065:树套树模板题。外层重量平衡树(这里选用的是替罪羊树)内层权值线段树。栋爷说外层线段树内层平衡树也可以做,可是我好像不大会写,可能是我太菜了吧。
#include <queue>
#include <cstdio>
#include <cstdlib>
#include <cassert>
#include <iostream>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
const int MAXN = 70000;
const int MAXM = 400*MAXN;
const double alpha = 0.78;
namespace segtree{
int cnt[MAXM + 5], ch[2][MAXM + 5];
queue<int>que;
void init() {for(int i=1;i<=MAXM;i++) que.push(i);}
void clear(int x) {
if( !x ) return ;
que.push(x);
clear(ch[0][x]); clear(ch[1][x]);
}
int newnode() {
assert(!que.empty());
int p = que.front(); que.pop();
cnt[p] = ch[0][p] = ch[1][p] = 0;
return p;
}
int merge(int x, int y) {
if( x == 0 && y == 0 ) return 0;
int p = newnode();
ch[0][p] = merge(ch[0][x], ch[0][y]);
ch[1][p] = merge(ch[1][x], ch[1][y]);
cnt[p] = cnt[x] + cnt[y];
return p;
}
void update(int &x, int l, int r, int p, int d) {
if( !x ) x = newnode(); cnt[x] += d;
if( l != r ) {
int m = (l + r) >> 1;
if( p <= m ) update(ch[0][x], l, m, p, d);
else update(ch[1][x], m + 1, r, p, d);
}
}
}
namespace victim{
struct node{
int rt, key, siz;
node *ch[2];
}pl[MAXN + 5], *ncnt, *NIL, *root;
void init() {
ncnt = NIL = pl;
NIL->ch[0] = NIL->ch[1] = NIL;
NIL->rt = NIL->key = NIL->siz = 0;
}
node *newnode(int k) {
node *p = (++ncnt);
p->ch[0] = p->ch[1] = NIL;
segtree::update(p->rt, 0, MAXN, k, 1);
p->key = k, p->siz = 1;
return p;
}
void pushup(node *x) {x->siz = x->ch[0]->siz + x->ch[1]->siz + 1;}
int v1[MAXN + 5], v2[MAXN + 5], cnt1, cnt2;
void get(node *x, int l, int r) {
if( l > r ) return ;
if( l == 1 && r == x->siz ) {
v2[++cnt2] = x->rt;
return ;
}
int p = x->ch[0]->siz + 1;
if( l <= p && p <= r ) v1[++cnt1] = x->key;
if( r <= p )
get(x->ch[0], l, min(r, p - 1));
else if( l >= p )
get(x->ch[1], max(l, p + 1) - p, r - p);
else
get(x->ch[0], l, min(r, p - 1)), get(x->ch[1], max(l, p + 1) - p, r - p);
}
int query(int l, int r, int k) {
cnt1 = cnt2 = 0, get(root, l, r);
int le = 0, ri = MAXN;
while( le != ri ) {
int mid = (le + ri) >> 1, tot1 = 0, tot2 = 0;
for(int i=1;i<=cnt1;i++) tot1 += (v1[i] <= mid);
for(int i=1;i<=cnt2;i++) tot2 += segtree::cnt[segtree::ch[0][v2[i]]];
if( tot1 + tot2 >= k ) {
ri = mid;
for(int i=1;i<=cnt2;i++)
v2[i] = segtree::ch[0][v2[i]];
}
else {
k -= tot2, le = mid + 1;
for(int i=1;i<=cnt2;i++)
v2[i] = segtree::ch[1][v2[i]];
}
}
return le;
}
void debug(node *x) {
if( x == NIL ) return ;
debug(x->ch[0]);
printf("%d %d : %d %d %d %d
", x->key, x - pl, x->ch[0] - pl, x->ch[1] - pl, x->siz, segtree::cnt[x->rt]);
debug(x->ch[1]);
}
int modify(node *x, int p, int v) {
segtree::update(x->rt, 0, MAXN, v, 1);
int k;
if( p <= x->ch[0]->siz ) k = modify(x->ch[0], p, v);
else if( p == x->ch[0]->siz + 1 ) k = x->key, x->key = v;
else k = modify(x->ch[1], p - x->ch[0]->siz - 1, v);
segtree::update(x->rt, 0, MAXN, k, -1);
return k;
}
node **re;
void insert(node *&x, int p, int v) {
if( x == NIL ) {
x = newnode(v);
return ;
}
segtree::update(x->rt, 0, MAXN, v, 1);
int d = (p > x->ch[0]->siz + 1);
insert(x->ch[d], d ? p - x->ch[0]->siz - 1 : p, v);
if( x->ch[d]->siz >= alpha * x->siz )
re = (&x);
pushup(x);
}
node *a[MAXN + 5]; int cnt;
void dfs(node *x) {
if( x == NIL ) return ;
dfs(x->ch[0]), a[++cnt] = x, dfs(x->ch[1]);
}
node *build(int l, int r) {
if( l > r ) return NIL;
int m = (l + r) >> 1;
node *x = a[m]; segtree::clear(x->rt);
x->ch[0] = build(l, m - 1), x->ch[1] = build(m + 1, r);
x->rt = segtree::merge(x->ch[0]->rt, x->ch[1]->rt);
segtree::update(x->rt, 0, MAXN, x->key, 1);
pushup(x); return x;
}
node *rebuild(node *x) {
int n = x->siz; cnt = 0, dfs(x);
return build(1, n);
}
void insert(int p, int v) {
re = 0, insert(root, p, v);
if( re ) (*re) = rebuild(*re);
}
}
int a[MAXN + 5];
victim::node *build(int l, int r) {
if( l > r ) return victim::NIL;
int m = (l + r) >> 1;
victim::node *x = victim::newnode(a[m]);
x->ch[0] = build(l, m - 1), x->ch[1] = build(m + 1, r);
x->rt = segtree::merge(x->rt, segtree::merge(x->ch[0]->rt, x->ch[1]->rt));
victim::pushup(x); return x;
}
int read() {
int x = 0; char ch = getchar();
while( ch < '0' || ch > '9' ) ch = getchar();
while( '0' <= ch && ch <= '9' ) x = 10*x + ch - '0', ch = getchar();
return x;
}
int main() {
// freopen("data.in", "r", stdin);
// freopen("data.out", "w", stdout);
segtree::init(); victim::init();
int n = read();
for(int i=1;i<=n;i++) a[i] = read();
victim::root = build(1, n);
int lastans = 0, m = read();
for(int i=1;i<=m;i++) {
char op[2]; scanf("%s", op);
if( op[0] == 'Q' ) {
int x = read(), y = read(), k = read();
// victim::debug(victim::root);
x ^= lastans, y ^= lastans, k ^= lastans;
printf("%d
", lastans = victim::query(x, y, k));
}
else if( op[0] == 'M' ) {
int x = read(), v = read();
x ^= lastans, v ^= lastans;
victim::modify(victim::root, x, v);
// victim::debug(victim::root);
}
else {
int x = read(), v = read();
x ^= lastans, v ^= lastans;
victim::insert(x, v);
// victim::debug(victim::root);
}
}
}
codeforces - 620F:信息不好合并,但支持单点插入,考虑莫队。单点插入只需要维护 trie 子树中的 min/max 判断是否有 ax <= ay 成立。发现不好删除,于是使用回滚莫队。时间复杂度 (O(nsqrt{n}log n))。
#include <stack>
#include <cstdio>
#include <vector>
#include <iostream>
#include <algorithm>
using namespace std;
typedef pair<int*, int> pii;
#define fi first
#define se second
#define mp make_pair
const int BLOCK = 225;
const int MAXN = 50000;
const int MAXK = (1 << 20);
int ch[2][2*MAXK + 5], s[MAXK + 5], cnt, rt;
int mn[2*MAXK + 5], mx[2*MAXK + 5];
int build(int dep) {
int p = (++cnt);
mn[p] = MAXK + 5, mx[p] = 0;
if( dep == -1 ) return p;
ch[0][p] = build(dep - 1);
ch[1][p] = build(dep - 1);
return p;
}
stack<pii>stk; int res;
void restore(int x) {
while( stk.size() > x ) {
pii t = stk.top(); stk.pop();
(*t.fi) = t.se;
}
}
void update_mx(int &p, int k) {
if( p < k ) stk.push(mp(&p, p)), p = k;
}
void update_mn(int &p, int k) {
if( p > k ) stk.push(mp(&p, p)), p = k;
}
int query_mn(int x, int dep, int k, int p) {
if( dep == -1 ) return 0;
int dir = ((k >> dep) & 1);
if( mn[ch[!dir][x]] < p )
return query_mn(ch[!dir][x], dep - 1, k, p) | (1 << dep);
else return query_mn(ch[dir][x], dep - 1, k, p);
}
int query_mx(int x, int dep, int k, int p) {
if( dep == -1 ) return 0;
int dir = ((k >> dep) & 1);
if( mx[ch[!dir][x]] > p )
return query_mx(ch[!dir][x], dep - 1, k, p) | (1 << dep);
else return query_mx(ch[dir][x], dep - 1, k, p);
}
void insert_mn(int x, int dep, int k, int p) {
update_mn(mn[x], p);
if( dep == -1 ) return ;
int dir = ((k >> dep) & 1);
insert_mn(ch[dir][x], dep - 1, k, p);
}
void insert_mx(int x, int dep, int k, int p) {
update_mx(mx[x], p);
if( dep == -1 ) return ;
int dir = ((k >> dep) & 1);
insert_mx(ch[dir][x], dep - 1, k, p);
}
void add(int x) {
insert_mn(rt, 19, s[x - 1], x - 1), insert_mx(rt, 19, s[x], x);
update_mx(res, query_mn(rt, 19, s[x], x));
update_mx(res, query_mx(rt, 19, s[x - 1], x - 1));
}
int n, m;
int le[MAXN + 5], ri[MAXN + 5], id[MAXN + 5], bcnt;
void init() {
for(int i=1;i<MAXK;i++)
s[i] = s[i - 1] ^ i;
rt = build(19);
for(int i=1;i<=n;i++) {
if( (i - 1) % BLOCK == 0 )
le[++bcnt] = i;
ri[bcnt] = i, id[i] = bcnt;
}
}
struct query{
int l, r, id; query() {}
query(int _l, int _r, int _i) : l(_l), r(_r), id(_i) {}
friend bool operator < (query a, query b) {
return a.r < b.r;
}
};
int a[MAXN + 5], ans[MAXN + 5];
vector<query>qry[MAXN + 5];
int main() {
scanf("%d%d", &n, &m), init();
for(int i=1;i<=n;i++) scanf("%d", &a[i]);
for(int i=1;i<=m;i++) {
int l, r; scanf("%d%d", &l, &r);
qry[id[l]].push_back(query(l, r, i));
}
for(int i=1;i<=bcnt;i++) {
sort(qry[i].begin(), qry[i].end());
int nwr = ri[i];
for(int j=0;j<qry[i].size();j++) {
int l = qry[i][j].l, r = qry[i][j].r;
if( r <= ri[i] ) {
for(int k=l;k<=r;k++) add(a[k]);
ans[qry[i][j].id] = res, restore(0);
}
else {
for(int k=nwr+1;k<=r;k++) add(a[k]); nwr = r;
int tim = stk.size();
for(int k=l;k<=ri[i];k++) add(a[k]);
ans[qry[i][j].id] = res, restore(tim);
}
}
restore(0);
}
for(int i=1;i<=m;i++)
printf("%d
", ans[i]);
}
codeforces - 468D:以重心为根进行跨子树的匹配,如果将点拆成两份,每个点的左边连向除自己所在子树以外的点,则题目要求即是字典序最小的完美匹配。根据 hall 定理推出存在完美匹配的条件,分前后两阶段考虑。注意重心可以自己匹配自己。
#include <set>
#include <queue>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 100000;
struct edge{
int to, dis; edge *nxt;
}edges[2*MAXN + 5], *adj[MAXN + 5], *ecnt = edges;
void addedge(int u, int v, int w) {
edge *p = (++ecnt);
p->to = v, p->dis = w, p->nxt = adj[u], adj[u] = p;
p = (++ecnt);
p->to = u, p->dis = w, p->nxt = adj[v], adj[v] = p;
}
ll ans; int siz[MAXN + 5], rt, n;
void get_rt(int x, int f) {
int mx = 0; siz[x] = 1;
for(edge *p=adj[x];p;p=p->nxt) {
if( p->to == f ) continue;
get_rt(p->to, x), siz[x] += siz[p->to];
ans += 2LL * min(siz[p->to], n - siz[p->to]) * p->dis;
mx = max(mx, siz[p->to]);
}
mx = max(mx, n - siz[x]);
if( 2*mx <= n ) rt = x;
}
int id[MAXN + 5], num[MAXN + 5], cnt;
void get_id(int x, int f, int i) {
id[x] = i, num[i]++;
for(edge *p=adj[x];p;p=p->nxt)
if( p->to != f ) get_id(p->to, x, i);
}
struct heap{
priority_queue<int>q1, q2;
void maintain() {
while( !q1.empty() && !q2.empty() && q1.top() == q2.top() )
q1.pop(), q2.pop();
}
bool empty() {maintain(); return q1.empty();}
int top() {maintain(); return q1.top();}
int size() {maintain(); return q1.size() - q2.size();}
void push(int x) {q1.push(x); maintain();}
void erase(int x) {q2.push(x); maintain();}
}h1, h2[MAXN + 5], h3, A, B;
bool tag[MAXN + 5];
int main() {
scanf("%d", &n);
for(int i=1;i<n;i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
addedge(u, v, w);
}
get_rt(1, 0), printf("%lld
", ans);
for(edge *p=adj[rt];p;p=p->nxt)
get_id(p->to, rt, ++cnt);
id[rt] = 0, num[0] = 0;
for(int i=1;i<=n;i++)
h2[id[i]].push(-i);
for(int i=0;i<=cnt;i++)
num[i] *= 2, h1.push(num[i]), h3.push(h2[i].top());
int nw = 1;
while( nw <= n && h1.top() < n - nw + 1 ) {
h1.erase(num[id[nw]]), num[id[nw]]--, h1.push(num[id[nw]]);
if( nw != rt ) h3.erase(h2[id[nw]].top());
int res = -h3.top(); printf("%d ", res), tag[res] = true;
h1.erase(num[id[res]]), num[id[res]]--, h1.push(num[id[res]]);
h3.erase(h2[id[res]].top()), h2[id[res]].erase(-res);
if( !h2[id[res]].empty() ) h3.push(h2[id[res]].top());
if( nw != rt ) h3.push(h2[id[nw]].top());
nw++;
}
if( nw <= n ) {
int mx;
for(int i=0;i<=cnt;i++)
if( num[i] == n - nw + 1 ) mx = i;
for(int i=1;i<=n;i++) {
if( tag[i] ) continue;
if( id[i] == mx ) A.push(-i);
else B.push(-i);
}
while( nw <= n ) {
if( id[nw] == mx ) {
int res = -B.top();
printf("%d ", res);
B.erase(-res);
}
else {
int res = -A.top();
printf("%d ", res);
A.erase(-res);
}
nw++;
}
}
}
bzoj - 4950:等于让剩下的最少。每行每列都必须保留一个最大值,让剩下的最少,就需要让最多的箱子同时充当该行该列的最大值。那么最大值相同的行列连边跑最大匹配即可。
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 100;
typedef long long ll;
int r, c;
int G[MAXN + 5][MAXN + 5], vis[MAXN + 5], lnk[MAXN + 5];
bool dfs(int x) {
for(int j=1;j<=c;j++) {
if( !vis[j] && G[x][j] ) {
vis[j] = true;
if( !lnk[j] || dfs(lnk[j]) ) {
lnk[j] = x;
return true;
}
}
}
return false;
}
int a[MAXN + 5][MAXN + 5], mxr[MAXN + 5], mxc[MAXN + 5];
int main() {
scanf("%d%d", &r, &c);
ll sum = 0, ans = 0;
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++) {
scanf("%d", &a[i][j]);
if( a[i][j] ) sum += a[i][j], ans++;
mxr[i] = max(mxr[i], a[i][j]), mxc[j] = max(mxc[j], a[i][j]);
}
for(int i=1;i<=r;i++) if( mxr[i] ) ans += mxr[i] - 1;
for(int j=1;j<=c;j++) if( mxc[j] ) ans += mxc[j] - 1;
for(int i=1;i<=r;i++)
for(int j=1;j<=c;j++)
if( mxr[i] == mxc[j] && a[i][j] )
G[i][j] = 1;
for(int i=1;i<=r;i++) {
if( !mxr[i] ) continue;
for(int j=1;j<=c;j++) vis[j] = false;
if( dfs(i) ) ans -= mxr[i] - 1;
}
printf("%lld
", sum - ans);
}
codeforces - 1250K:根据贪心知识,安排完 HD 投影仪后,所需普通投影仪数量最少为同时存在的 seminar 最大数量。离散化后可以确定出每个段至少有多少 seminar 需要使用 HD 投影仪。建一条链跑网络流,如果有活动 (l, r) 则连边 l->r,lecture 把流量下界设为 1。限制一下链上每条边的容量即可满足上述条件。
#include <queue>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 300;
const int INF = (1 << 30);
struct FlowGraph{
#define MAXV 4*MAXN
#define MAXE 10*MAXV
struct edge{
int to, cap, flow;
edge *rev, *nxt;
}edges[MAXE + 5], *adj[MAXV + 5], *cur[MAXV + 5], *ecnt;
void clear() {
for(int i=0;i<=MAXV;i++) adj[i] = NULL;
ecnt = edges;
}
edge *addedge(int u, int v, int c) {
// printf("! %d %d %d
", u, v, c);
edge *p = (++ecnt), *q = (++ecnt);
p->to = v, p->cap = c, p->flow = 0;
p->nxt = adj[u], adj[u] = p;
q->to = u, q->cap = 0, q->flow = 0;
q->nxt = adj[v], adj[v] = q;
p->rev = q, q->rev = p;
return p;
}
int d[MAXV + 5], s, t;
int que[MAXV + 5], hd, tl;
bool relabel() {
for(int i=s;i<=t;i++)
d[i] = INF, cur[i] = adj[i];
d[que[hd = tl = 1] = t] = 0;
while( hd <= tl ) {
int x = que[hd++];
for(edge *p=adj[x];p;p=p->nxt)
if( p->rev->cap > p->rev->flow && d[x] + 1 < d[p->to] )
d[que[++tl] = p->to] = d[x] + 1;
}
return !(d[s] == INF);
}
int aug(int x, int tot) {
if( x == t ) return tot;
int sum = 0;
for(edge *&p=cur[x];p;p=p->nxt)
if( p->cap > p->flow && d[p->to] + 1 == d[x] ) {
int del = aug(p->to, min(tot - sum, p->cap - p->flow));
sum += del, p->flow += del, p->rev->flow -= del;
if( sum == tot ) break;
}
return sum;
}
int max_flow(int _s, int _t) {
s = _s, t = _t; int flow = 0;
while( relabel() )
flow += aug(s, INF);
return flow;
}
}G;
int n, m, x, y, S, T;
int a[MAXN + 5], b[MAXN + 5], p[MAXN + 5], q[MAXN + 5];
int s[4*MAXN + 5], t[4*MAXN + 5], d[4*MAXN + 5], cnt;
FlowGraph::edge *e[MAXN + 5];
bool get() {
for(int i=1;i<=cnt;i++) s[i] = t[i] = 0;
for(int i=1;i<=m;i++) s[p[i]]++, s[q[i]]--;
for(int i=1;i<=cnt;i++) s[i] += s[i-1];
for(int i=1;i<=cnt;i++) s[i] = max(0, s[i] - y);
for(int i=1;i<=n;i++) t[a[i]]++, t[b[i]]--;
for(int i=1;i<=cnt;i++) t[i] += t[i-1];
for(int i=1;i<cnt;i++) {
if( s[i] + t[i] > x ) {
puts("NO");
return false;
}
if( x != s[i] + t[i] ) G.addedge(i, i + 1, x - (s[i] + t[i]));
}
S = 0, T = cnt + 1;
G.addedge(S, 1, x), G.addedge(cnt, T, x);
for(int i=1;i<=m;i++) e[i] = G.addedge(p[i], q[i], 1);
for(int i=1;i<=n;i++) G.addedge(S, b[i], 1), G.addedge(a[i], T, 1);
if( G.max_flow(S, T) == x + n ) {
puts("YES");
return true;
}
else {
puts("NO");
return false;
}
}
struct node{
int l, r, x; node() {}
node(int _l, int _r, int _x) : l(_l), r(_r), x(_x) {}
friend bool operator < (node a, node b) {
return a.l < b.l;
}
}c[2*MAXN + 5]; int tot;
int ans[2*MAXN + 5];
priority_queue<pair<int, int> >que;
void func(int p) {
while( !que.empty() ) que.pop();
sort(c + 1, c + tot + 1);
for(int i=1;i<=tot;i++) {
if( !que.empty() && -que.top().first <= c[i].l ) {
int q = que.top().second; que.pop();
que.push(make_pair(-c[i].r, ans[c[i].x] = q));
}
else que.push(make_pair(-c[i].r, ans[c[i].x] = (++p)));
}
}
void solve() {
G.clear(), cnt = 0;
scanf("%d%d%d%d", &n, &m, &x, &y);
for(int i=1;i<=n;i++) scanf("%d%d", &a[i], &b[i]), d[++cnt] = a[i], d[++cnt] = b[i];
for(int i=1;i<=m;i++) scanf("%d%d", &p[i], &q[i]), d[++cnt] = p[i], d[++cnt] = q[i];
sort(d + 1, d + cnt + 1), cnt = unique(d + 1, d + cnt + 1) - d - 1;
for(int i=1;i<=n;i++) {
a[i] = lower_bound(d + 1, d + cnt + 1, a[i]) - d;
b[i] = lower_bound(d + 1, d + cnt + 1, b[i]) - d;
}
for(int i=1;i<=m;i++) {
p[i] = lower_bound(d + 1, d + cnt + 1, p[i]) - d;
q[i] = lower_bound(d + 1, d + cnt + 1, q[i]) - d;
}
if( get() ) {
for(int i=1;i<=n;i++) c[i] = node(a[i], b[i], i);
tot = n;
for(int i=1;i<=m;i++)
if( e[i]->flow ) c[++tot] = node(p[i], q[i], n + i);
func(0);
tot = 0;
for(int i=1;i<=m;i++)
if( !e[i]->flow ) c[++tot] = node(p[i], q[i], n + i);
func(x);
for(int i=1;i<=n+m;i++)
printf("%d ", ans[i]);
puts("");
}
}
int main() {
int t; scanf("%d", &t);
while( t-- ) solve();
}
topcoder - SRM719D1L2:负数变成 0 可以看成是删除已经访问过的点。那么就是选择若干无祖先关系的点往下走的最大权值和,基础树形 dp。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
class OwaskiAndTree{
public:
int f[5005], g[5005];
vector<int>G[5005]; int a[5005], N;
void dfs(int x) {
f[x] = a[x], g[x] = 0;
for(int i=0;i<(int)G[x].size();i++) {
int to = G[x][i]; dfs(to);
f[x] += f[to], g[x] += g[to];
}
f[x] = max(f[x], 0), g[x] = max(g[x], f[x]);
}
int maximalScore(vector<int>parent, vector<int>pleasure) {
N = (int)pleasure.size();
for(int i=0;i<N;i++) a[i] = pleasure[i];
for(int i=1;i<N;i++) G[parent[i - 1]].push_back(i);
dfs(0); return g[0];
}
};
51nod - 1355:考虑在唯一分解下 gcd 本质为指数取 min,而 lcm 为取 max。根据 min-max 容斥,可得 (lcm(S) = frac{prod_{Tsubset S}^{|T|奇}gcd(T)}{prod_{Tsubset S}^{|T|偶}gcd(T)})。一个经典结论 (gcd(f_i, f_j) = f_{gcd(i, j)})。因此莫比乌斯反演求出每个斐波那契数的指数即可。
#include <cstdio>
const int MAXN = 50000;
const int MAX = 1000000;
const int MOD = 1000000007;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return (1LL * x * y % MOD);}
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=mul(b,b))
if( i & 1 ) ret = mul(ret, b);
return ret;
}
int f[MAX + 5], pw2[MAX + 5];
void init() {
pw2[0] = 1;
for(int i=1;i<=MAX;i++)
pw2[i] = 2LL*pw2[i - 1]%(MOD - 1);
f[0] = 0, f[1] = 1;
for(int i=2;i<=MAX;i++)
f[i] = add(f[i - 1], f[i - 2]);
}
int a[MAXN + 5], b[MAX + 5], c[MAX + 5], ro[MAX + 5], re[MAX + 5];
int main() {
init();
int N; scanf("%d", &N);
for(int i=1;i<=N;i++)
scanf("%d", &a[i]), b[a[i]]++;
for(int i=1;i<=MAX;i++) {
c[i] = 0;
for(int j=i;j<=MAX;j+=i)
c[i] += b[j];
}
for(int i=MAX;i>=1;i--) {
if( c[i] == 0 ) continue;
ro[i] = pw2[c[i] - 1], re[i] = ro[i] - 1;
for(int j=2*i;j<=MAX;j+=i) {
ro[i] = (ro[i] + (MOD - 1) - ro[j]) % (MOD - 1);
re[i] = (re[i] + (MOD - 1) - re[j]) % (MOD - 1);
}
}
int ans = 1;
for(int i=1;i<=MAX;i++) {
int pw = ((ro[i] - re[i]) % (MOD - 1) + (MOD - 1)) % (MOD - 1);
ans = mul(ans, pow_mod(f[i], pw));
}
printf("%d
", ans);
}
loj - 3020:由条件可得 (f(a, b) = f(d, d) imesfrac{a}{d} imesfrac{b}{d}),其中 d = gcd(a, b)。因此答案为 (sum_{d=1}^{k}f(d, d)sum_{i=1}^{lfloor frac{k}{d} floor}sum_{j=1}^{lfloor frac{k}{d} floor}[gcd(i, j) = 1] imes i imes j)。后面可以欧拉函数预处理 + 整除分块,用 O(1) 查询的分块维护 f(d, d) 前缀和可以做到 (O(msqrt{n}))。
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int BLOCK = 2000;
const int MAXN = 4000000;
const int MOD = 1000000007;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return (1LL * x * y % MOD);}
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=mul(b,b))
if( i & 1 ) ret = mul(ret, b);
return ret;
}
int gcd(int x, int y) {return y == 0 ? x : gcd(y, x % y);}
int m, n;
bool nprm[MAXN + 5];
int f[MAXN + 5], phi[MAXN + 5], prm[MAXN + 5], pcnt;
void sieve() {
phi[1] = 1;
for(int i=2;i<=n;i++) {
if( !nprm[i] ) prm[++pcnt] = i, phi[i] = i - 1;
for(int j=1;i*prm[j]<=n;j++) {
nprm[i*prm[j]] = true;
if( i % prm[j] == 0 ) {
phi[i*prm[j]] = phi[i]*prm[j];
break;
}
else phi[i*prm[j]] = phi[i]*phi[prm[j]];
}
}
for(int i=1;i<=n;i++)
f[i] = add(f[i - 1], mul(mul(i, i), phi[i]));
}
int tg[MAXN + 5], c[MAXN + 5], s[MAXN + 5];
int le[MAXN + 5], ri[MAXN + 5], id[MAXN + 5], bcnt;
void init() {
sieve();
for(int i=1;i<=n;i++) {
if( (i - 1) % BLOCK == 0 )
le[++bcnt] = i;
ri[bcnt] = i, id[i] = bcnt, c[i] = mul(i, i), s[i] = add(s[i - 1], c[i]);
}
}
void modify(int p, int d) {
for(int i=p;i<=ri[id[p]];i++) s[i] = add(s[i], d);
for(int i=id[p]+1;i<=bcnt;i++) tg[i] = add(tg[i], d);
}
int sum(int l, int r) {
int L = add(s[l-1], tg[id[l-1]]);
int R = add(s[r], tg[id[r]]);
return sub(R, L);
}
int query(int k) {
int ret = 0;
for(int i=1;i<=k;i++) {
int j = (k/(k/i));
ret = add(ret, mul(sum(i, j), f[k/i]));
i = j;
}
return ret;
}
int main() {
scanf("%d%d", &m, &n), init();
for(int i=1;i<=m;i++) {
int a, b, k; ll x; scanf("%d%d%lld%d", &a, &b, &x, &k);
int d = gcd(a, b); x /= (a/d), x /= (b/d), x %= MOD;
modify(d, sub(x, c[d])), c[d] = x;
printf("%d
", query(k));
}
}
codeforces - 286E:首先肯定是选择 a 的子集。如果合法,那么任意 a 的子集之和都可以表示成 a 中两个数之和。标记 a 中任意两个数之和。如果一个 a 中元素被标记,则它可以不被选入;如果一个在 m 以内非 a 中元素被标记,则不合法。可以构造 (f(x) = sum x^{a_i}) 然后平方。
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int MOD = 998244353;
const int MAXN = (1 << 21);
const int G = 3;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
int pow_mod(int b, int p) {
int ret = 1;
for(int i=p;i;i>>=1,b=mul(b,b))
if( i & 1 ) ret = mul(ret, b);
return ret;
}
int w[22], iw[22];
void init() {
for(int i=0;i<22;i++) {
w[i] = pow_mod(G, (MOD - 1) / (1 << i));
iw[i] = pow_mod(w[i], MOD - 2);
}
}
int length(int n) {
int len; for(len = 1; len < n; len <<= 1);
return len;
}
void ntt(int *A, int n, int type) {
for(int i=0,j=0;i<n;i++) {
if( i < j ) swap(A[i], A[j]);
for(int k=(n>>1);(j^=k)<k;k>>=1);
}
for(int i=1;(1<<i)<=n;i++) {
int s = (1 << i), t = (s >> 1);
int u = (type == 1 ? w[i] : iw[i]);
for(int j=0;j<n;j+=s) {
for(int k=0,p=1;k<t;k++,p=mul(p,u)) {
int x = A[j+k], y = mul(p, A[j+k+t]);
A[j+k] = add(x, y), A[j+k+t] = sub(x, y);
}
}
}
if( type == -1 ) {
int iv = pow_mod(n, MOD - 2);
for(int i=0;i<n;i++)
A[i] = mul(A[i], iv);
}
}
vector<int>ans;
int f[MAXN + 5]; bool tag[MAXN + 5];
int n, m;
int main() {
init(); scanf("%d%d", &n, &m);
for(int i=1;i<=n;i++) {
int x; scanf("%d", &x);
tag[x - 1] = true, f[x - 1] = 1;
}
int len = length(m + m - 1);
ntt(f, len, 1);
for(int i=0;i<len;i++)
f[i] = mul(f[i], f[i]);
ntt(f, len, -1);
for(int i=1;i<=m;i++) {
bool p = (i >= 2 ? f[i - 2] : false);
if( tag[i - 1] ) {
if( !p ) ans.push_back(i);
}
else {
if( p ) {
puts("NO");
return 0;
}
}
}
puts("YES");
printf("%d
", (int)ans.size());
for(int i=0;i<(int)ans.size();i++)
printf("%d ", ans[i]);
}
atcoder - AGC027D:(两年前我不会做的构造题,然而我现在我也不会)先特判 n = 2。黑白染色,使黑格为相邻白格的 lcm + 1。白格设置成 所在主对角线对应的素数 * 所在副对角线对应的素数,黑格则为前 2n 个素数中某 4 个素数之积 + 1。一大一小地填素数可以保证范围在 10^15 内。
#include <cstdio>
#include <cassert>
using namespace std;
typedef long long ll;
const ll INF = ll(1E15);
const int MAXN = 100000;
const int dx[] = {0, 0, 1, -1};
const int dy[] = {1, -1, 0, 0};
bool nprm[MAXN + 5];
int prm[MAXN + 5], pcnt;
void init() {
for(int i=2;i<=MAXN;i++) {
if( !nprm[i] ) prm[++pcnt] = i;
for(int j=1;i*prm[j]<=MAXN;j++) {
nprm[i*prm[j]] = true;
if( i % prm[j] == 0 ) break;
}
}
}
ll gcd(ll x, ll y) {
return y == 0 ? x : gcd(y, x % y);
}
ll a[505][505], p[1005], q[1005];
int main() {
init(); int N; scanf("%d", &N);
if( N == 2 ) {
printf("4 7
23 10
");
return 0;
}
int cnt = 0;
for(int i=1;i<=N;i+=2)
p[i] = prm[++cnt], q[i] = prm[++cnt];
for(int i=N-(N&1);i>=0;i-=2)
p[i] = prm[++cnt], q[i] = prm[++cnt];
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
if( (i + j) % 2 == 0 )
a[i][j] = p[(i + j)/2] * q[(i + N - j + 1)/2];
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++) {
if( (i + j) % 2 == 0 ) continue;
a[i][j] = 1;
for(int o=0;o<4;o++) {
int x1 = i + dx[o], y1 = j + dy[o];
if( x1 < 1 || x1 > N || y1 < 1 || y1 > N ) continue;
a[i][j] = a[i][j] / gcd(a[i][j], a[x1][y1]) * a[x1][y1];
}
a[i][j]++, assert(a[i][j] <= INF);
}
for(int i=1;i<=N;i++)
for(int j=1;j<=N;j++)
printf("%lld%c", a[i][j], j == N ? '
' : ' ');
}
atcoder - AGC025D:如果 D 为奇数,直接黑白染色任取一色即可;否则如果 D = 2*奇数,可以黑白染色将黑白格点分成两部分,旋转 45° 并放缩,在两块图中 D' = 奇数,就是一开始的情况;否则如果 D = 2^k*奇数,这样递归 k 次即可。两个 D 可以把点分成 4 个类,最大那个一定满足条件。
#include <cstdio>
#include <vector>
#include <iostream>
using namespace std;
const int MAXN = 600;
const int MAXM = MAXN*MAXN;
vector<pair<int, int> >ans[4];
bool clr[20][MAXM + 5];
int x[MAXM + 5], y[MAXM + 5], id[MAXN + 5][MAXN + 5], cnt;
int main() {
int N, D1, D2, p1 = 0, p2 = 0; scanf("%d%d%d", &N, &D1, &D2);
while( D1 % 2 == 0 ) D1 /= 2, p1++;
while( D2 % 2 == 0 ) D2 /= 2, p2++;
for(int i=0;i<2*N;i++)
for(int j=0;j<2*N;j++)
id[i][j] = (++cnt), x[cnt] = i, y[cnt] = j;
for(int o=0;o<20;o++)
for(int i=1;i<=cnt;i++) {
clr[o][i] = ((x[i] + y[i]) % 2 != 0);
int tx = (x[i] + y[i] + clr[o][i]) / 2, ty = (x[i] - y[i] + clr[o][i]) / 2;
x[i] = tx, y[i] = ty;
}
for(int i=0;i<2*N;i++)
for(int j=0;j<2*N;j++) {
int x = id[i][j];
ans[clr[p1][x] | (clr[p2][x] << 1)].push_back(make_pair(i, j));
}
int res = 0;
for(int i=0;i<4;i++)
if( ans[i].size() > ans[res].size() )
res = i;
for(int i=0;i<N*N;i++)
printf("%d %d
", ans[res][i].first, ans[res][i].second);
}
atcoder - AGC022E:首先把所有 "000" 消成 "0"。从最左边开始,如果最左边出现了 "11",则一定合法;如果最左边出现了 "1001",则应该消成 "10";否则直接消掉最左边 3 个。最后如果没有 "11" 但是只剩 "1" 也合法。上述过程可以表示成一个自动机,然后 dp 即可:
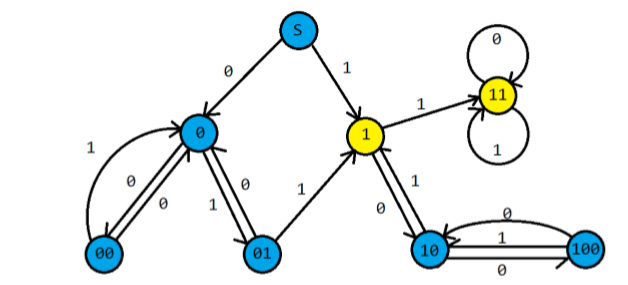
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 300000;
const int MOD = int(1E9) + 7;
const int trans[2][8] = {
{1, 3, 5, 1, 1, 6, 5, 7},
{2, 4, 7, 1, 2, 2, 5, 7}
};
int f[2][8], n; char s[MAXN + 5];
int main() {
scanf("%s", s), n = strlen(s);
f[0][0] = 1;
for(int i=0;i<n;i++) {
for(int j=0;j<8;j++)
f[1][j] = f[0][j], f[0][j] = 0;
if( s[i] != '0' ) {
for(int j=0;j<8;j++)
f[0][trans[1][j]] = (f[0][trans[1][j]] + f[1][j]) % MOD;
}
if( s[i] != '1' ) {
for(int j=0;j<8;j++)
f[0][trans[0][j]] = (f[0][trans[0][j]] + f[1][j]) % MOD;
}
}
printf("%d
", (f[0][2] + f[0][7]) % MOD);
}
loj - 2257:对 L/G 进行唯一分解,设有 k 个质因子。L/G 的因数可分为 3^k 类,表示每种质因子的指数是下界/上界/不是上下界。然后就是个容斥 + 高维前缀和,求出 “哪些质因子需要上界/下界” 的 4^k 种答案。注意询问时要先判断是否 <= N。
#include <cmath>
#include <cstdio>
#include <algorithm>
using namespace std;
const int MAXN = 100000;
const int MOD = 1000000007;
const int INV2 = (MOD + 1) / 2;
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
int N, G, L;
int prm[10], pw[10], cnt, tot;
int f[1<<10][1<<10];
void dfs(int d, int x, int s1, int s2) {
if( d == cnt ) {
f[s1][s2] += (x*G <= N);
return ;
}
int p = 1, i;
dfs(d + 1, x*p, s1 | (1 << d), s2);
for(i=1,p*=prm[d];i<pw[d];i++,p*=prm[d])
dfs(d + 1, x*p, s1, s2);
dfs(d + 1, x*p, s1, s2 | (1 << d));
}
int pw2[MAXN + 5];
void divide(int x) {
int sq = (int)sqrt(x);
for(int i=2;i<=sq;i++)
if( x % i == 0 ) {
prm[cnt] = i;
while( x % i == 0 )
pw[cnt]++, x /= i;
cnt++;
}
if( x != 1 ) prm[cnt] = x, pw[cnt] = 1, cnt++;
dfs(0, 1, 0, 0);
tot = (1 << cnt);
/*
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( f[s1][s2] ) printf("%d %d : %d
", s1, s2, f[s1][s2]);
puts("");
*/
for(int i=0;i<cnt;i++)
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( (s2 >> i) & 1 ) f[s1][s2] += f[s1][s2^(1<<i)];
for(int i=0;i<cnt;i++)
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( (s1 >> i) & 1 ) f[s1][s2] += f[s1^(1<<i)][s2];
pw2[0] = 1; for(int i=1;i<=MAXN;i++) pw2[i] = mul(2, pw2[i-1]);
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
f[s1][s2] = pw2[f[s1][s2]];
for(int i=0;i<cnt;i++)
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( (s2 >> i) & 1 ) f[s1][s2] = sub(f[s1][s2], f[s1][s2^(1<<i)]);
for(int i=0;i<cnt;i++)
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( (s1 >> i) & 1 ) f[s1][s2] = sub(f[s1][s2], f[s1^(1<<i)][s2]);
for(int i=0;i<cnt;i++)
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( !((s2 >> i) & 1) ) f[s1][s2] = add(f[s1][s2], f[s1][s2^(1<<i)]);
for(int i=0;i<cnt;i++)
for(int s1=0;s1<tot;s1++)
for(int s2=0;s2<tot;s2++)
if( !((s1 >> i) & 1) ) f[s1][s2] = add(f[s1][s2], f[s1^(1<<i)][s2]);
}
int get(int x) {
int s1 = 0, s2 = 0;
for(int i=0;i<cnt;i++) {
int p = 0;
while( x % prm[i] == 0 )
x /= prm[i], p++;
if( p != 0 ) s1 |= (1 << i);
if( p != pw[i] ) s2 |= (1 << i);
}
return mul(f[s1][s2], INV2);
}
int main() {
scanf("%d%d%d", &N, &G, &L), divide(L / G);
int Q; scanf("%d", &Q);
for(int i=1;i<=Q;i++) {
int X; scanf("%d", &X);
if( X % G == 0 && L % X == 0 && X <= N )
printf("%d
", get(X / G));
else puts("0");
}
}
loj - 2178:每一种路径方案的平方和 -> 任意选两条有序相同路径的方案。因此作一个 O(n^4) 的 dp 即可。实现上使用记忆化搜索最佳。注意到路径交换起点终点依然合法,因此可以少枚举一半的方向,可以由 64 次减少到 32 次(据说可以减少到 16 次,不大清楚)。不然过不了 bzoj 的数据。
#include <cstdio>
#include <algorithm>
using namespace std;
#define rep(i, x, y) for(i = x; i <= y; i++)
const int MOD = 1000000009;
const int dxl[] = {0, 0, 0, 0, -1, -1, -1, 0};
const int dxr[] = {1, 1, 1, 0, 0, 0, 0, 0};
const int dyl[] = {0, 0, -1, -1, -1, 0, 0, 0};
const int dyr[] = {1, 0, 0, 0, 0, 0, 1, 1};
inline int add(int x, int y) {return (x + y >= MOD ? x + y - MOD : x + y);}
inline int sub(int x, int y) {return (x - y < 0 ? x - y + MOD : x - y);}
inline int mul(int x, int y) {return 1LL * x * y % MOD;}
char s[30][30];
int f[30][30][30][30], n, m;
int o1, o2;
int dp(int x1, int y1, int x2, int y2) {
if( s[x1][y1] != s[x2][y2] ) return 0;
if( f[x1][y1][x2][y2] != -1 ) return f[x1][y1][x2][y2];
int ans = 1;
int dx1, dy1, dx2, dy2;
rep(dx1, dxl[o1], dxr[o1]) rep(dy1, dyl[o1], dyr[o1]) {
if( dx1 == 0 && dy1 == 0 ) continue;
int _x1 = x1 + dx1, _y1 = y1 + dy1;
if( _x1 < 0 || _x1 >= n || _y1 < 0 || _y1 >= m ) continue;
rep(dx2, dxl[o2], dxr[o2]) rep(dy2, dyl[o2], dyr[o2]) {
if( dx2 == 0 && dy2 == 0 ) continue;
int _x2 = x2 + dx2, _y2 = y2 + dy2;
if( _x2 < 0 || _x2 >= n || _y2 < 0 || _y2 >= m ) continue;
ans = add(ans, dp(_x1, _y1, _x2, _y2));
}
}
return f[x1][y1][x2][y2] = ans;
}
int main() {
scanf("%d%d", &n, &m);
for(int i=0;i<n;i++) scanf("%s", s + i);
int ans = 0;
rep(o1, 0, 4 - 1) rep(o2, 0, 8 - 1) {
int i, j, p, q;
rep(i, 0, n - 1) rep(j, 0, m - 1)
rep(p, 0, n - 1) rep(q, 0, m - 1)
f[i][j][p][q] = -1;
int del = 0;
rep(i, 0, n - 1) rep(j, 0, m - 1)
rep(p, 0, n - 1) rep(q, 0, m - 1)
del = add(del, mul(2, dp(i, j, p, q)));
if( (o1 + o2) & 1 ) ans = sub(ans, del);
else ans = add(ans, del);
}
printf("%d
", ans);
}
zoj - 3808:长得一副 (phi(x)) 样,于是就 powerful number + 杜教筛,时间复杂度为杜教筛复杂度 (O(n^{frac{2}{3}}))(跑得还没有min-25筛快,丢人)。小心 MLE。
#include <cstdio>
#include <algorithm>
typedef long long ll;
const int SQRT = 100000;
const int MAXN = 2000000;
const int MAX = 1000000000;
ll phi[MAXN + 5]; bool nprm[MAXN + 5];
int prm[MAXN + 5], pcnt;
ll g[35], h[SQRT + 5][35];
void init() {
phi[1] = 1;
for(int i=2;i<=MAXN;i++) {
if( !nprm[i] ) prm[++pcnt] = i, phi[i] = i - 1;
for(int j=1;i*prm[j]<=MAXN;j++) {
nprm[i*prm[j]] = true;
if( i % prm[j] == 0 ) {
phi[i*prm[j]] = phi[i]*prm[j];
break;
}
else phi[i*prm[j]] = phi[i]*phi[prm[j]];
}
}
for(int i=1;i<=MAXN;i++)
phi[i] += phi[i-1];
for(int i=1;i<=SQRT;i++) {
g[0] = h[i][0] = 1, g[1] = prm[i] - 1;
ll p = 1LL * prm[i] * prm[i];
for(int j=2;p<=MAX;j++,p*=prm[i]) {
h[i][j] = p - 1, g[j] = g[j-1]*prm[i];
for(int k=0;k<j;k++)
h[i][j] -= h[i][k]*g[j-k];
}
}
}
ll sp[SQRT + 5];
ll sum1(int n) {return 1LL * n * (n + 1) / 2;}
int a[SQRT + 5], id1[SQRT + 5], id2[SQRT + 5], cnt, n;
int id(int x) {return (x <= SQRT ? id1[x] : id2[n / x]);}
void get() {
cnt = 0;
for(int i=1;i<=n;i=n/(n/i)+1) {
int p = n / i; a[++cnt] = p;
if( p <= SQRT ) id1[p] = cnt;
else id2[n / p] = cnt;
}
for(int i=cnt;i>=1;i--) {
int m = a[i];
if( m <= MAXN ) {
sp[i] = phi[m];
continue;
}
sp[i] = sum1(m);
for(int j=2;j<=m;j++) {
int p = (m / j), k = (m / p);
sp[i] -= sp[id(p)]*(k - j + 1);
j = k;
}
}
}
ll ans;
void dfs(int x, int d, int k) {
ans += k*sp[id(n / x)];
for(int i=d;;i++) {
if( 1LL*x*prm[i]*prm[i] > n ) break;
ll p = x*prm[i]*prm[i];
for(int j=2;p<=n;j++,p*=prm[i])
dfs(p, i + 1, k*h[i][j]);
}
}
int main() {
init();
while( scanf("%d", &n) == 1 )
get(), ans = 0, dfs(1, 1, 1), printf("%lld
", ans);
}