@description@
烟花表演是最引人注目的节日活动之一。在表演中,所有的烟花必须同时爆炸。为了确保安全,烟花被安置在远离开关的位置上,通过一些导火索与开关相连。导火索的连接方式形成一棵树,烟花是树叶,如图 1所示。火花从开关出发,沿导火索移动。每当火花抵达一个分叉点时,它会扩散到与之相连的所有导火索,继续燃烧。导火索燃烧的速度是一个固定常数。图 1展示了六枚烟花 {E1, E2, E3, E4, E5, E6} 的连线布局,以及每根导火索的长度。图中还标注了当在时刻 0 从开关点燃火花时,每一发烟花的爆炸时间。
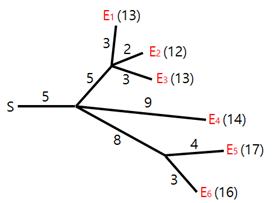
Hyunmin 为烟花表演设计了导火索的连线布局。不幸的是,在他设计的布局中,烟花不一定同时爆炸。我们希望修改一些导火索的长度,让所有烟花在同一时刻爆炸。例如,为了让图 1中的所有烟花在时刻 13 爆炸,我们可以像图 2中左边那样调整导火索长度。类似地,为了让图 1中的所有烟花在时刻 14 爆炸,我们可以像图 2中右边那样调整长度。
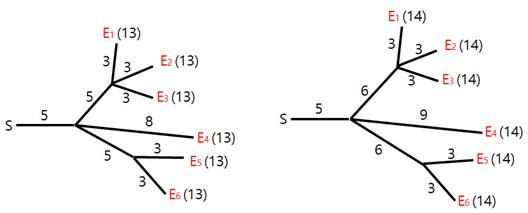
修改导火索长度的代价等于修改前后长度之差的绝对值。例如,将图 1中布局修改为图 2,左边布局的总代价为 6,而将图 1中布局修改为图 2右边布局的总代价为 5。
导火索的长度可以被减为 0,同时保持连通性不变。
给定一个导火索的连线布局,你需要编写一个程序,去调整导火索长度,让所有的烟花在同一时刻爆炸,并使得代价最小。
输入格式
所有的输入均为正整数。令 N 代表分叉点的数量,M 代表烟花的数量。分叉点从 1 到 N 编号,编号为 1 的分叉点是开关。烟花从 N+1 到 N+M 编号。
输入格式如下:
N M
P2 C2
P3 C2
...
PN CN
PN+1 CN+1
...
PN+M CN+M
其中 Pi 满足 1<=Pi<i,代表和分叉点或烟花 i 相连的分叉点。Ci 代表连接它们的导火索长度 (1<=Ci<=10^9)。除开关外,每个分叉点和多于 1 条导火索相连,而每发烟花恰好与 1 条导火索相连。
输出格式
输出调整导火索长度,让所有烟花同时爆炸,所需要的最小代价。
样例输入
4 6
1 5
2 5
2 8
3 3
3 2
3 3
2 9
4 4
4 3
样例输出
5
数据范围与提示
1 <= N + M <= 3*10^5。
@solution@
显然答案呈凸函数形式。
如果相类似的题目做得多了,倒是很容易发现答案的凸性质:代价与最终修改的时间成凸函数。
而且,叶子的凸性质也很容易发现:叶子的代价与时间成绝对值函数。
然后呢?也许我们可以通过儿子的凸函数合并出当前结点的凸函数。
这个涉及到两个过程:将儿子的凸函数对应位置相加(即当前结点到父亲的边不变);然后考虑当前结点到父亲的边。
这个凸函数有点特殊啊:
它有一个斜率为 0 的区间 [L, R](假设 L 可以与 R 相等);并且其他部分的斜率的绝对值 >= 1。
因此,当前结点到父亲的边必须非负的前提下,假如这条边的边权为 w,原函数为 f(x),则新函数 f'(x) 为:
第一个情况就是原函数向上平移(对应当前结点到父亲的边必须非负)。
第三个情况就是把斜率为 0 的区间向右下平移。
第二个情况是一段斜率为 -1 的直线,第四个情况是一段斜率为 1 的直线,对应修改当前结点到父亲的边。
其实就是将函数 L 以后的部分抛弃,然后接斜率为 -1, 0, 1 的直线。
那说了这么多,我们也不能暴力维护啊。
这个凸函数有点特殊啊:
从左到右,函数的每一段的斜率都是逐渐增大,且每次增量为 1(我们将单点 [L, L] 也视为一条直线)。
并且,这个函数的最小斜率为叶子数量的相反数(因为每个叶子提供一个 -1,每次又会两个子树的函数相加,到父亲的边也不会影响最小斜率)
并且,这个函数 f 的截距 f(0) = ∑w(u, v)(对应将所有边边权都改成 0)。
那么,只要知道每个分段的点的横坐标,就可以还原出整个函数!
我们用一个数据结构来维护每个函数分段点的横坐标。
这个数据结构要支持:
(1)合并(对应儿子函数的相加)。
(2)弹出斜率 >= 0 的点(可以从右往左弹,直到点数 = 叶子数 + 1)。
插入什么的就不提了。可以发现最合适的应该是可并堆。
最后得到了 f(x),答案应该是什么呢?
最小值肯定落在斜率为 0 的地方。根据 f(0) = ∑w(u, v) 与斜率逐渐增大的性质,可以得到:
啊,你问我上述的证明。
充分利用这个凸包的特殊性,归纳验证即可。
@accepted code@
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 300000;
struct edge{
int to; ll key;
edge *nxt;
}edges[MAXN + 5], *adj[MAXN + 5], *ecnt = &edges[0];
void addedge(int u, int v, ll w) {
edge *p = (++ecnt);
p->to = v, p->key = w, p->nxt = adj[u], adj[u] = p;
}
struct Heap{
struct node{
ll key; int siz, dis;
node *ch[2];
}pl[2*MAXN + 5], *ncnt, *NIL;
Heap() {
ncnt = NIL = &pl[0];
NIL->siz = NIL->dis = NIL->key = 0;
NIL->ch[0] = NIL->ch[1] = NIL;
}
void pushup(node *x) {
x->siz = x->ch[0]->siz + x->ch[1]->siz + 1;
if( x->ch[1]->dis > x->ch[0]->dis ) swap(x->ch[0], x->ch[1]);
x->dis = x->ch[1]->dis + 1;
}
node *newnode(ll k) {
node *p = (++ncnt);
p->key = k, p->ch[0] = p->ch[1] = NIL;
pushup(p); return p;
}
node *merge(node *x, node *y) {
if( x == NIL ) return y;
if( y == NIL ) return x;
if( x->key < y->key ) swap(x, y);
x->ch[1] = merge(x->ch[1], y);
pushup(x); return x;
}
void erase(node *&x) {x = merge(x->ch[0], x->ch[1]);}
void insert(node *&x, ll k) {x = merge(x, newnode(k));}
}T;
int siz[MAXN + 5], N, M;
Heap::node *dfs(int x) {
siz[x] = (x > N);
int cnt = 0; Heap::node *ret = T.NIL;
for(edge *p=adj[x];p;p=p->nxt) {
Heap::node *tmp = dfs(p->to);
ll R = tmp->key; T.erase(tmp);
ll L = tmp->key; T.erase(tmp);
T.insert(tmp, L + p->key), T.insert(tmp, R + p->key);
ret = T.merge(tmp, ret);
siz[x] += siz[p->to];
}
while( ret->siz > siz[x] + 1 ) T.erase(ret);
return ret;
}
int main() {
scanf("%d%d", &N, &M);
ll ans = 0;
for(int i=2;i<=N+M;i++) {
int P; ll C; scanf("%d%lld", &P, &C);
addedge(P, i, C), ans += C;
}
Heap::node *rt = dfs(1); T.erase(rt);
while( rt != T.NIL )
ans -= rt->key, T.erase(rt);
printf("%lld
", ans);
}
@details@
一开始想错了,把叶子个数的限制想成了子树大小。。。
然后这个题显然是需要 long long 的。