@0 - 参考资料@
@1 - 问题引入@
一个经典问题:
一正方形分成4格,2着色,有多少种方案?
其中,经过转动相同的图象算同一方案。
假如不考虑转动,各种方案如下所示。
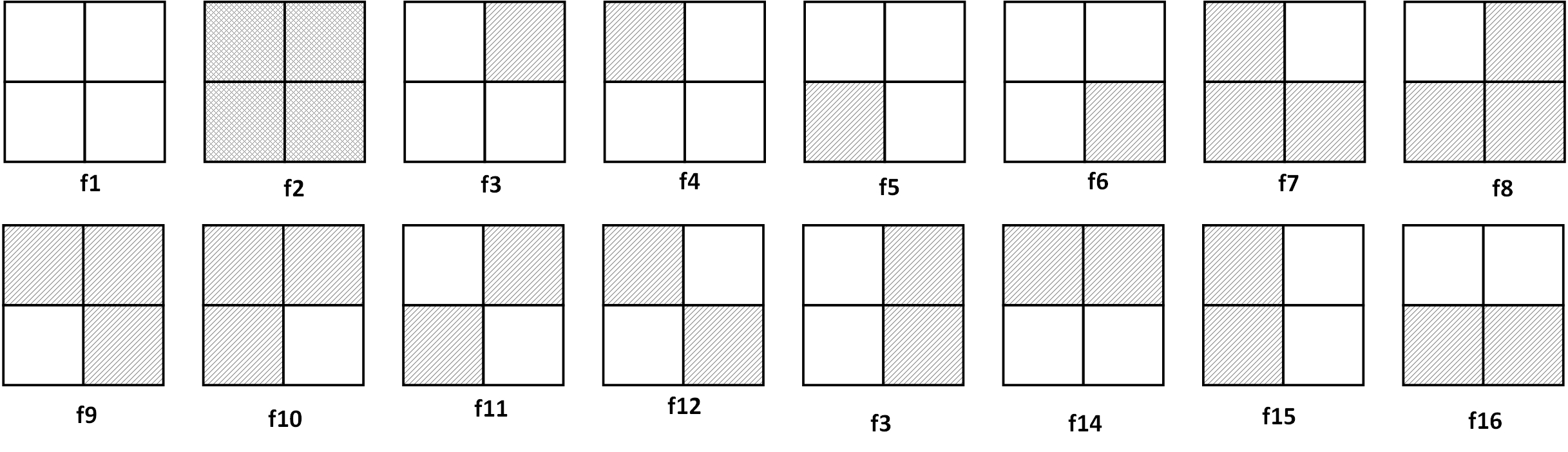
首先可以发现,转动的角度只有 4 种:0°,90°,180°,270°。
然后可以得到,每一次转动可以将一个方案唯一映射成另一个方案(可以是自身)。
于是我们可以用一个置换 p 描述一次旋转的效果,其中 p[i] 表示第 i 种方案被映射成了第 p[i] 种方案。
在这个例子中,4 种置换(0°,90°,180°,270°)构成了一个置换群。
(什么是置换群。。。emmm可以自行左转百度)
(以下的记法都是不严谨的,因为是根据我自己的记忆写的)
如果置换 f 使得元素 i 映射成 j,我们就记作 (f:i -> j)。
对于置换群 G,如果存在 (fin G),以及 (f:x -> y),我们就称 x, y 为等价类。
显然这个等价关系满足传递性、自反性、对称性(对应群的几个性质)。
那么我们相等于求在置换群G的作用下的等价类个数。
@2 - burnside引理@
先抛结论:
我们称对于 f,满足 f:x -> x 的 x 为 f 作用下的不动点。记 c(f) 表示 f 的不动点个数。
则 G 作用下的等价类个数为:
update in 2020/07/12:看了一会儿抽代教材结果只学会了几个高级名词,回来补充一下比较正式的证明。
定义轨道:({
m Orb}(s) ={x|exists p,p(x)=s})(少数几个形象化的名词),即群 (G) 作用下的等价类。
定义稳定化子(稳定子群):({
m Stab}(s) = {p|p(s)=s})。看名字可以发现它是 (G) 的子群。
({ m burnside}) 引理等价于证明 (|{ m Orb}(s)| imes |{ m Stab}(s)| = |G|)(update:仔细一想好像并不等价。。。算了不太重要)
只需证明 ({ m Stab}(s)) 的陪集集合与 ({ m Ord}(s)) 之间存在双射,即可由拉格朗日定理直接得到上述结论。
思考一下 ({
m Stab}(s)) 的左陪集的实际意义:({g|g(x)=s,xin{
m Orb(s)}})(右陪集即 ({g|g(s)=x,xin {
m Orb(s)}}))。严谨证明就不给了2333。
其实我之前写的非正式证明定义的 (S_{i,j}) 本质就是陪集,(S_{i,i}) 本质就是 ({ m Stab(s)})。
证明是我自己BB的,与主流证法不大一样(我也记不到主流证法了),所以可能不够简便。
引入(一个非常不严谨的)记法:记 (S_{i, j}) 表示将 i 映射到 j 的置换组成的集合。
首先证明几个引理:
引理 1:(|S_{i, j}| = |S_{j, i}|)
证明:等价于证明 (|S_{i, j}| le |S_{j, i}|) 且 (|S_{j, i}| le |S_{i, j}|)。
只需考虑 (|S_{i, j}| le |S_{j, i}|),另一半同理可证。
对于 (f in S_{i, j}),它的逆元 (f^{-1} in S_{j, i})。且根据置换群的性质,每个元素的逆元是唯一的,且不同元素的逆元不同。
所以 (S_{j, i}) 至少含有 (|S_{i, j}|) 个元素——即它们的逆元。
引理 2:若 (S_{i, j}) 不为空,则 (|S_{i, j}| = |S_{i, i}|)
证明:只需证明 (|S_{i, j}| le |S_{i, i}|) 且 (|S_{i, i}| le |S_{i, j}|)。
从 (S_{j, i}) 中任选一个元素 (f),(f) 与 (S_{i, j}) 中的每一个 (g) 相乘得到 (f*g)。
显然有 (f*g in S_{i, i}),且 g 不相同时,得到的结果也一定不同,所以 (|S_{i, j}| le |S_{i, i}|)。
然后依然是从 (S_{j, i}) 中任选一个元素 (f),(f) 与 (S_{i, i}) 中的每一个 (g) 相乘得到 (f*g)。
有 (f*g in S_{j, i}),且 g 不相同时,得到的结果也不同。故又得到 (|S_{i, i}| le |S_{j, i}| = |S_{i, j}|)(由引理 1)。
引理 3:一个等价类中的不动点数量总和 = |G|。
证明:设该等价类 (E = {x_1, x_2, ..., x_k})。
则有 (sum_{i=1}^{k}|S_{x_1, x_i}| = |G|)(每个在 G 中的置换一定会把 (x_1) 映射成等价类中的某个数)。
根据引理 1 + 引理 2,可以得到 (sum_{i=1}^{k}|S_{x_i, x_i}| = |G|),于是得证。
有了引理 3,就可以推导出我们的 burnside 引理的正确性了,因为不动点的总数 = 等价类个数*|G|。
@3 - pólya定理@
(注意是 pólya 定理而不是 polya 定理,虽然这不重要不过还是要看起来专业点)
burnside 引理提出了一种统计等价类的一般方法,而 pólya 定理提出了在染色问题下的不动点具体计算方法。
在我们一开始给出的问题中,假如我们要老老实实地算,要算 2^(2+2) 个方案在置换下是否为不动点。
当数据范围增大时,方案数急剧增大,burnside引理就失去了意义。
我们不妨把 2*2 个点拿出来,构建置换群。以下假设可用颜色数量为 m。
我们将每个置换循环分解,则这个置换作用下的不动点肯定是相同循环内的元素涂相同颜色。
设置换 f 的循环分解后共有 c(f) 个循环,则 f 作用下不动点数量为 (m^{c(f)})。
则 G 作用下不动点数量为:
这样就可以将指数级复杂度化为多项式复杂度。
@4 - pólya定理的生成函数形式@
可以发现,pólya 定理是非常显然的。但同时 pólya 定理也是非常普遍应用的。
但是!如果结合万能的生成函数,我们就可以得到一些更有趣的东西。
还是一开始的典型例子,假如我们想要知道固定黑色格子有多少个时,本质不同的方案数。
这时候我们就需要利用生成函数了。
假如置换 f 进行循环分解得到 k 个循环,每个循环的循环节大小分别为 x1, x2, ..., xk。
则这个置换 f 对应的生成函数为 (F(f) = prod_{i=1}^{k}(b^{x_i} + w^{x_i}))。其中 b, w 就是形式变量。
整个置换群 G 的生成函数为:
则 G 中的 (b^i*w^j) 项的系数等于涂 i 格黑色与 j 格白色的方案数。
比如对于我们一开始的例子,生成函数为:
验证一下就可以发现它的正确性。